作者：Eugene Wang

如果我們想要對二維矢量進行旋轉，我們需要知道旋轉點和旋轉角度。如果要進行三維旋轉，我們需要指定旋轉軸和旋轉角度。那么，我們可以進行四維旋轉嗎？或者說，我們可以進行更復雜的旋轉嗎？事實上，我們可以將其簡化為，有一個n維向量，然后將這個向量旋轉到另一個n維向量，我們將用更系統(tǒng)的方式來表達旋轉。

首先，我們先來看看旋轉的一些性質(zhì)。第一個性質(zhì)是旋轉是線性變換，這種線性意味著兩個方程：和。如果你在二維平面畫出這些向量，你就可以驗證它們。

由于旋轉的線性屬性，我們可以把旋轉寫成矩陣的形式：n維向量的旋轉等于旋轉矩陣R乘以n維向量。剩下的目標就是找到旋轉矩陣R，使得。

接下來，我們要來講旋轉的第二個性質(zhì)：如果我們只是單純旋轉，向量的長度和向量之間的角度應該保持不變。這一性質(zhì)意味著，兩個向量的點積在旋轉前后保持不變。也就是說，如果原來是v·w，那么兩個向量旋轉后就變成了Rv·Rw，兩個點積是相等的：。

對于實數(shù)向量，我們也可以將點積寫為第一個向量的轉置乘以第二個向量：。我們也可以將等式右邊進行一下變換，就可以得到。因為這對于所有的向量v和w都是成立的，所以中間的就是單位矩陣。

因此，歸結起來第二個性質(zhì)就是滿足的旋轉矩陣，我們把滿足該性質(zhì)的所有矩陣的集合表示為，O代表正交，n代表矩陣R的階。

然而，長度和角度保持不變不僅僅只有旋轉能做得到，反射也能做到這一點。因此，與反射對應的矩陣也將是屬于O(n)的。所以，我們需要旋轉的第三個性質(zhì)，即它不會改變順序。我的意思是，假如原本從向量v到向量w是逆時針，那么經(jīng)過反射后就變成了順時針，而旋轉卻不會做出這樣的改變。因此，根據(jù)線性代數(shù)的知識，我們知道旋轉矩陣R的行列式應該為正的，所以。

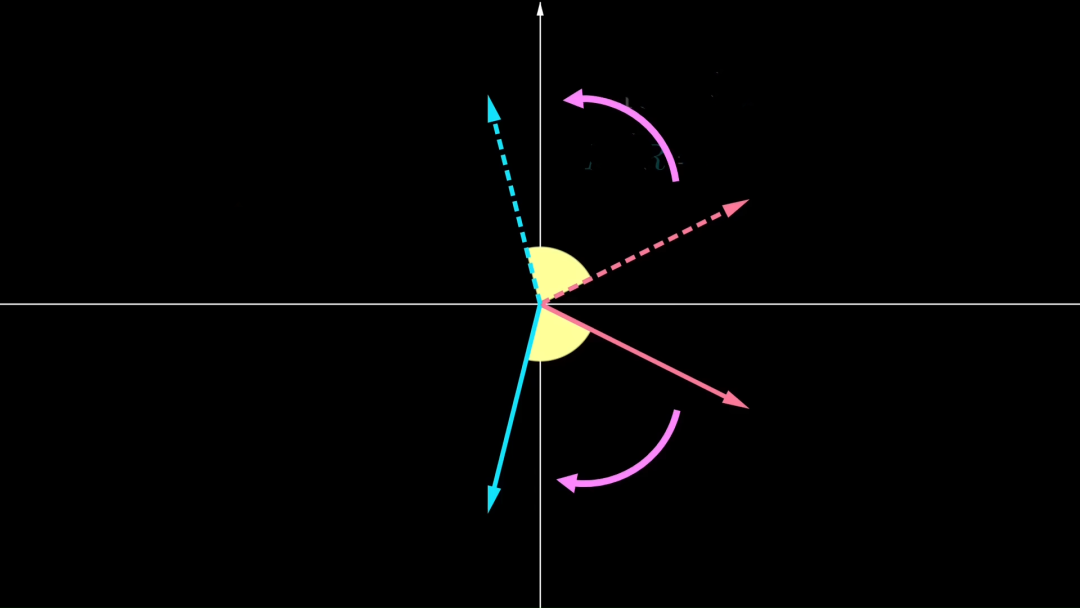
因此，如果一個矩陣已經(jīng)屬于O(n)，并且它的行列式為1，那么它就屬于SO(n)：。這里的S代表特殊的，對應于行列式為1的附加要求。

以上的討論都是針對實向量，如果我們要旋轉復數(shù)向量的話，我們只要稍微進行修改就行。首先，我們把旋轉矩陣R替換成矩陣U，它們之間的區(qū)別是U是一個復矩陣。其次，從第二個性質(zhì)我們得到了，現(xiàn)在我們要把它改成，其中意味著我們除了轉置之外還取復共軛。最后，我們還有：和。

這樣一來，我們就將旋轉推廣到了更高的維度和復數(shù)。雖然這些旋轉矩陣很難直接去求解，但幸運的是，這些矩陣的集合，無論是O(n)、SO(n)、U(n)還是SU(n)，都會形成稱為李群的東西，這些都可以通過李理論去求解。

編輯：黃飛