在二維中,我們可以在平面上放置一個網格,然后每個點都用一對數字來表示。
這種結構并不特定于二維,我們還可以添加第三維度。
但是,我們不能再為第四個維度的空間繪制網格了,不過依然可以寫下四維向量,它們只是一行四個數字。
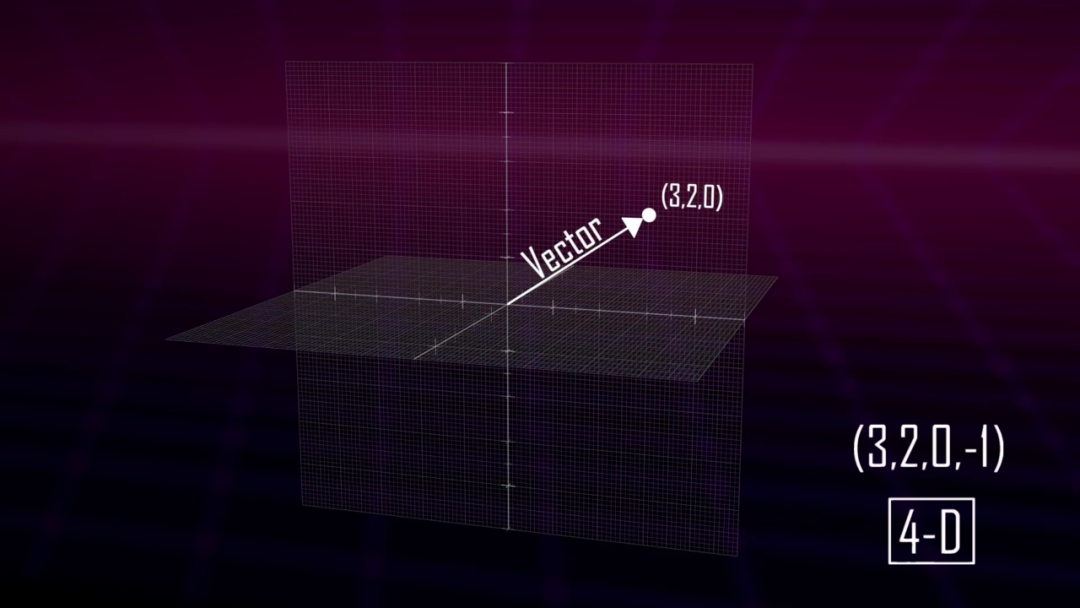
實際上,我們可以構建任何維數的向量。有了更高維度的向量,我們就可以用它們來研究幾何學,例如構建更高維度的平面或立方體。
雖然我們不能直接繪制這些高維對象,但我們可以將它們的投影繪制到低維中。
高維幾何聽起來很天真,但這是朝著數學抽象思維邁出的一大步。
它標志著現在所謂的“純數學”的開始,即為數學本身而追求的數學,不一定是因為它有應用。
然而,抽象的數學概念往往對物理學有用。
這些高維幾何對物理學家來說真的很方便,因為在物理學中,我們通常不僅要處理位于特定位置的事物,還要處理也會沿特定方向移動的事物。
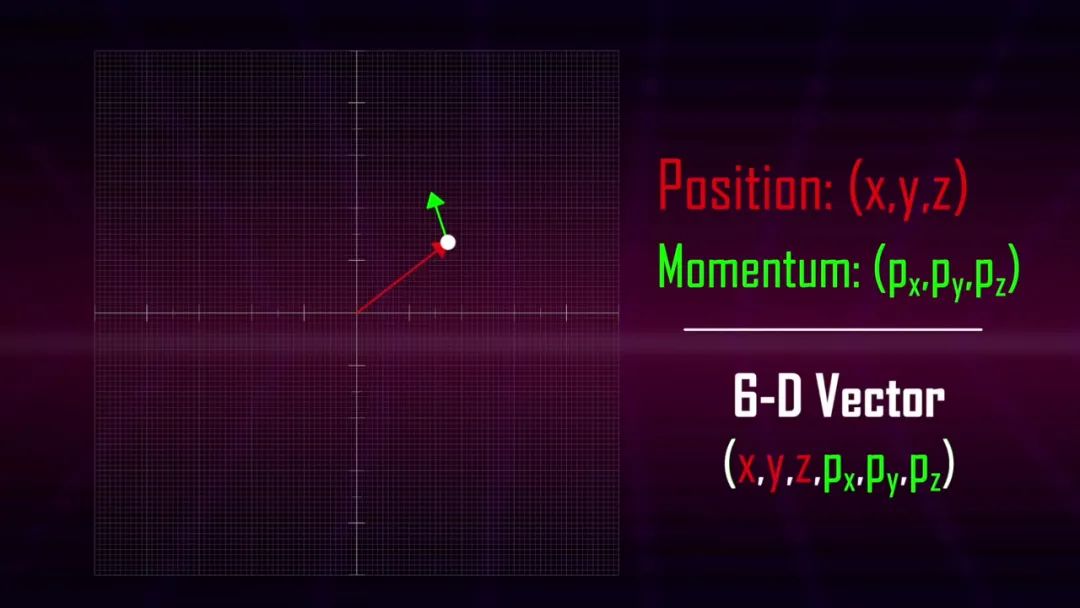
例如,如果我們有一個粒子要描述它的作用,我們分別需要位置和動量的三維信息,因此實際上每個粒子都由一個六維空間中的向量來描述。
這個六維空間稱為相空間,通過處理相空間,物理學家變得習慣于處理更高維度的幾何形狀。
自然而然,他們開始懷疑我們所居住的實際空間是否可以擁有更多的維度。
卡魯扎-克萊因理論
這個想法最初是由芬蘭物理學家貢納爾·努德斯特倫提出的,他在1914年嘗試使用空間的第四維度來描述引力,但沒有成功。
弄清楚引力如何工作的是愛因斯坦,他告訴我們引力不需要額外的空間維度。
空間的三個維度就足夠了,只是你必須添加一個時間維度,并讓所有這些維度都彎曲。
但是,如果你不需要額外的引力維度,那么我們可以將它用于其他用途。
1921年,西奧多·卡魯扎寫了一篇論文,其中他試圖使用空間的第四維度來描述電磁力,但卻沒有解釋第四維度在哪里。
幾年后,奧斯卡·克萊因解決了這個問題,他認為空間的第四維度必須蜷縮得很小。
這樣一來,我們就很難發現它存在,也就符合我們的現實感受。
這種認為電磁力是由空間的第四維卷曲引起的想法現在被稱為卡魯扎-克萊因理論。

這種需要額外維度的想法非常有效,它完全用幾何方式解釋了力。
可能正因為如此,愛因斯坦晚年才相信幾何是物理學基礎統一理論的關鍵。但至少到目前為止,還沒有人成功給出大一統理論。
理論缺陷
我們實際上并沒有使用卡魯扎-克萊因理論來替代電磁學,這是因為該理論存在一些嚴重的問題。
第一個問題是,雖然附加維度的幾何形狀正確地為我們提供了電場和磁場,但它并沒有為我們提供帶電粒子,例如電子。
第二個問題是額外維度的半徑不穩定,如果我們擾動它,半徑可能會開始增加,并產生我們應該看到卻沒有看到的可觀察后果。
第三個問題是理論沒有量子化,沒有人想出如何量子化幾何而不遇到問題。
但是,我們卻可以毫無問題地量子化普通電磁學。
當然,我們今天也知道電磁力實際上與弱力相結合成所謂的電弱力。
有趣的是,這種結合對卡魯扎-克萊因理論來說不是問題。
事實上,在1960年代,物理學家理查德·克納表明,人們不僅可以用卡魯扎-克萊因理論做電磁學,還可以為弱力和強力應用卡魯扎-克萊因理論,我們只需要添加更多維度就行。
對于弱力,我們需要另外兩個空間維度。而對于強力,我們需要另外四個空間維度。
所以總的來說,我們現在有1個時間維度,3個引力維度,1個電磁力維度,2個弱力維度,4個強力維度,總共有11個維度。
巧合的是,1981年愛德華·威滕注意到11維恰好也是M理論需要的維數。
審核編輯:劉清
-
處理器
+關注
關注
68文章
19349瀏覽量
230296 -
向量機
+關注
關注
0文章
166瀏覽量
20888 -
電磁場
+關注
關注
0文章
792瀏覽量
47302
原文標題:用幾何描繪物理學的統一理論:卡魯扎-克萊因理論
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 淺析用幾何描繪物理學的統一理論
淺析用幾何描繪物理學的統一理論










評論