介紹

當直流電源電壓施加到電容器上時，電容器緩慢充電，最后到達完全充電位置。此時，電容器的充電電壓等于電源電壓。

在這里，只要施加電壓，電容器就充當能量源。電容器在充滿電后不允許電流 （i） 通過它們。流過電路的電流取決于電容器極板中的電荷量，并且電流與施加到電路的電壓變化率成正比。即 i = dQ/dt = C dV（t）/dt。

如果將交流電源電壓施加到電容器電路，則電容器根據電源電壓的頻率速率連續充電和放電。交流電路中電容器的電容取決于施加在其上的電源電壓的頻率。在交流電路中，當電源電壓相對于時間連續變化時，電容器允許電流。

交流電容器電路

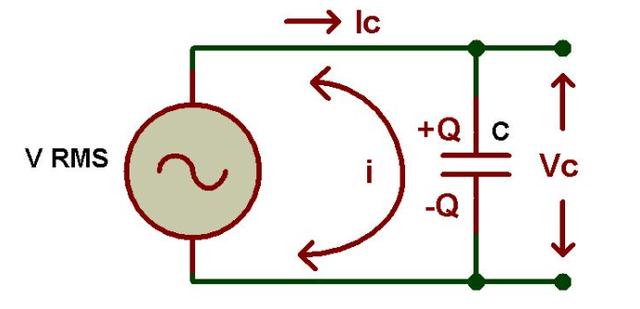
在上面的電路中，我們觀察到電容器直接連接到交流電源電壓。在這里，電容器根據電源電壓的變化不斷充電和放電，因為交流電源電壓值不斷增加和減少。我們都知道，流過電路的電流與施加電壓的變化率成正比。

在這里，如果電源電壓從正半周期越過其值到負半周期，則充電電流具有高值，反之亦然。即在 00和 1800在正弦波信號中。當正弦波中的電源電壓越過其最大或最小峰值（Vm）時，流過電容器的電流具有其最小值。因此，我們可以說流過電路的充電電流是最大或最小，具體取決于正弦波中的電源電壓電平。

交流電容相量圖

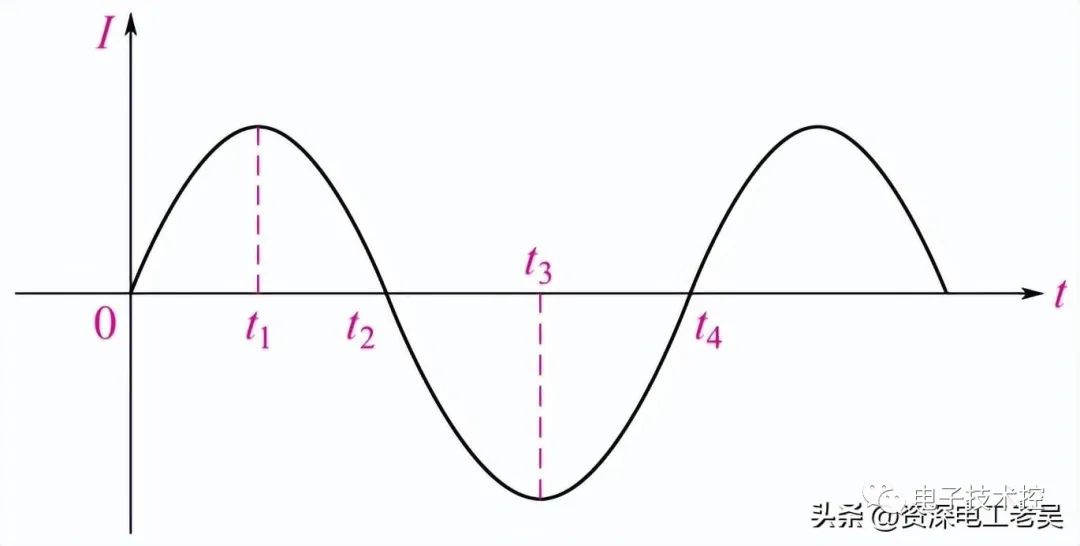
交流電容器的相量圖如上圖所示，這里的電壓和電流以正弦波形式表示。在上圖中，我們觀察到在 00充電電流處于最大值，因為電壓在正方向上緩慢增加。90歲時0沒有電流流過電容器，因為此時電源電壓處于其最大峰值。

在 1800點電壓緩慢降至零，電流在負方向上處于最大值。充電再次達到360的最大值0，因為此時電源電壓處于最小值。

從上圖中的波形可以看出，電流領先電壓900.因此，我們可以說，在理想的電容器電路中，交流電壓滯后電流900.

容抗

我們知道，流過電容器的電流與施加電壓的變化率成正比，但電容器也提供某種形式的電阻，與電阻器一樣。交流電路中電容器的這種電阻稱為容抗或通常稱為電抗。電容電抗是電容器的特性，它反對交流電路中的電流流動。它用符號Xc表示，并以歐姆為單位測量，與類似電阻相同。

我們需要一些額外的能量來超過容抗來為電路中的電容器充電。該值與電容值和電源電壓頻率成反比。

Xc∝ 1/c 和 Xc∝ 1/f。

容抗方程和影響它們的參數將在下面討論。

容抗，

XC = 1/2πfC = 1/ωC

這里

XC = 電容器的電抗

f = 頻率（以赫茲為單位）

C = 電容器的電容，單位為法拉

Ω （歐米茄） = 2πf

從上式中我們了解到，當頻率和電容值較低時，容抗很高，在此階段，電容器充當完美的電阻器。如果電源電壓的頻率高，則電容器的電抗值較低，并且在此階段電容器充當良導體。從上式可以清楚地看出，如果頻率為無窮大，則電抗為零，而當頻率為零時，電抗值為無窮大。

容抗頻率

上圖顯示了電源電壓的容抗、電流和頻率之間的關系。在這里，我們觀察到，如果頻率低，則電抗很高。充電電流隨著頻率的增加而增加，因為電壓的變化率隨著時間的推移而增加。電抗在頻率為零時處于無窮大值，反之亦然。

交流電容示例No1

求出流過具有連接到 3V 和 660Hz 電源的 40uF 電容器的電路的電流的均方根值。

XC = 1/2πfC

f = 40HZ

C = 3uF

Vrms = 660V

現在

XC = 1/（2 × 3.14 × 40HZ × 3 × 10-6) = 1326?

IRMS = Vrms/XC = 660V/1326Ω = 497mA

交流電容示例No2

求出流過具有連接到 5V 和 880Hz 電源的 50uF 電容器的電路的電流的均方根值。

f = 50HZ

C = 5uF

Vrms = 880V

XC = 1/（2 × 3.14 × 50HZ × 5 × 10-6） = 636Ω

Irms = Vrms/XC = 880V/636? = 1.38 A

從上述兩個例子中，我們觀察到電容器的電抗取決于電源電壓的頻率，并且呈成反比關系。在示例1中，電抗為1326HZ的頻率為40Ω，但當頻率增加到636HZ時，電抗值降低到50Ω，如示例2所示。