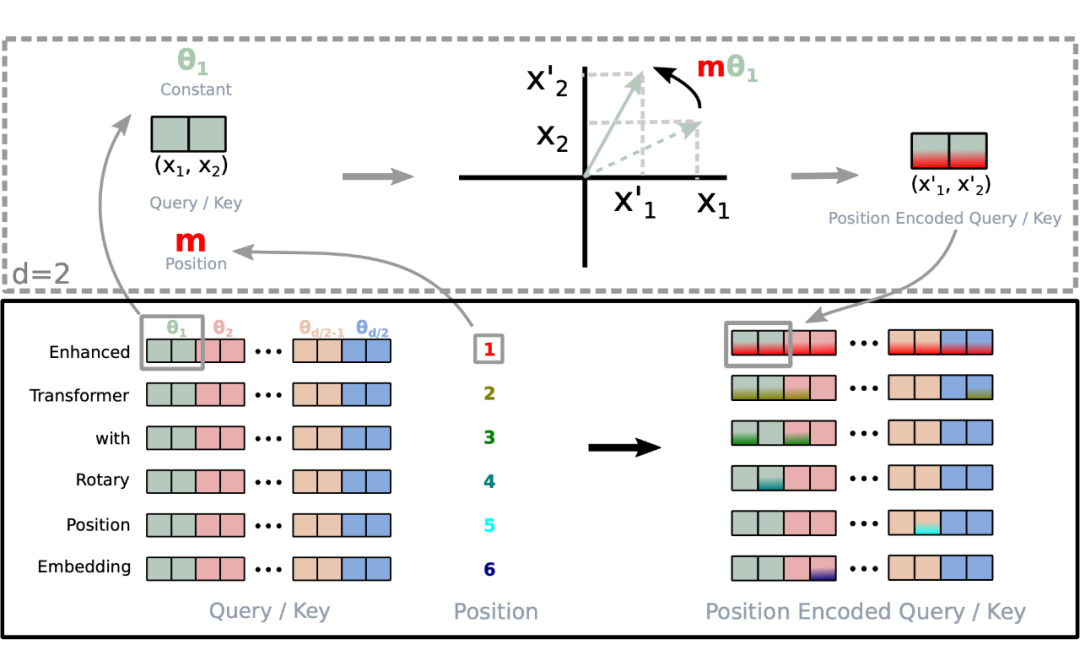
旋轉(zhuǎn)位置編碼(Rotary Position Embedding,RoPE)是論文 Roformer: Enhanced Transformer With Rotray Position Embedding 提出的一種能夠?qū)⑾鄬?duì)位置信息依賴集成到 self-attention 中并提升 transformer 架構(gòu)性能的位置編碼方式。而目前很火的 LLaMA、GLM 模型也是采用該位置編碼方式。
和相對(duì)位置編碼相比,RoPE 具有更好的外推性,目前是大模型相對(duì)位置編碼中應(yīng)用最廣的方式之一。
備注:什么是大模型外推性?
外推性是指大模型在訓(xùn)練時(shí)和預(yù)測(cè)時(shí)的輸入長(zhǎng)度不一致,導(dǎo)致模型的泛化能力下降的問(wèn)題。例如,如果一個(gè)模型在訓(xùn)練時(shí)只使用了 512 個(gè) token 的文本,那么在預(yù)測(cè)時(shí)如果輸入超過(guò) 512 個(gè) token,模型可能無(wú)法正確處理。這就限制了大模型在處理長(zhǎng)文本或多輪對(duì)話等任務(wù)時(shí)的效果。
旋轉(zhuǎn)編碼RoPE
1.1 基本概念
在介紹 RoPE 之前,先給出一些符號(hào)定義,以及基本背景。
首先定義一個(gè)長(zhǎng)度為 的輸入序列為:
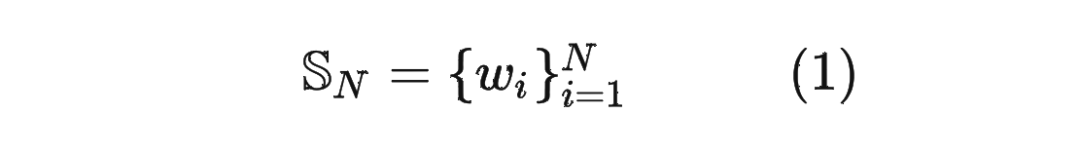
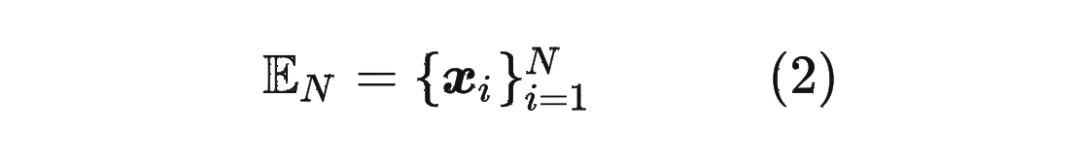
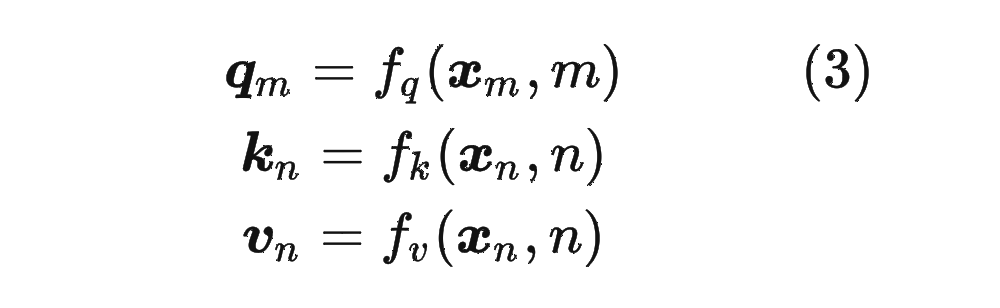
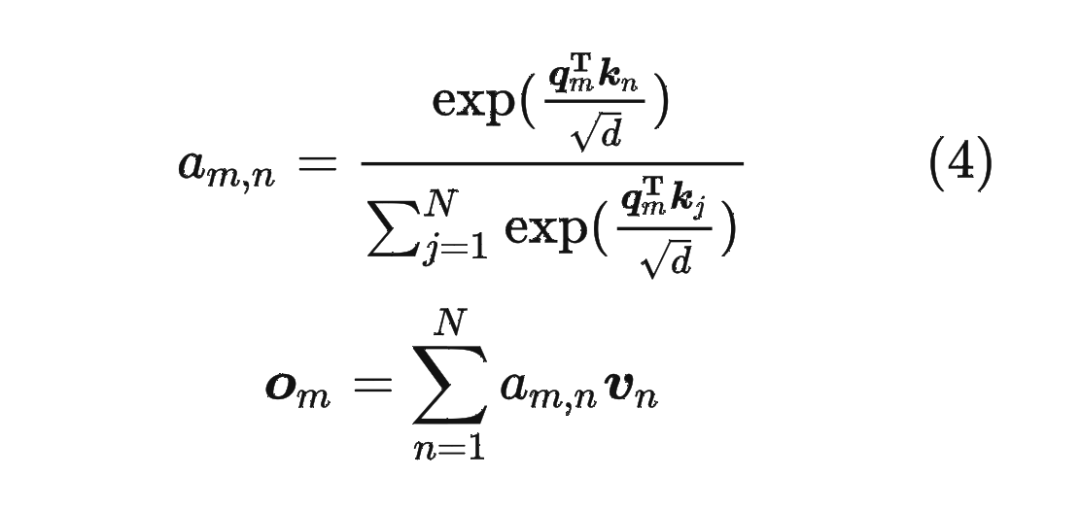
1.2 絕對(duì)位置編碼
對(duì)于位置編碼,常規(guī)的做法是在計(jì)算 query,key 和 value 向量之前,會(huì)計(jì)算一個(gè)位置編碼向量 加到詞嵌入 上,位置編碼向量 同樣也是 維向量,然后再乘以對(duì)應(yīng)的變換矩陣 :
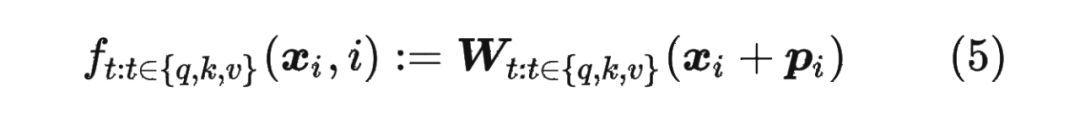
而經(jīng)典的位置編碼向量 的計(jì)算方式是使用 Sinusoidal 函數(shù):
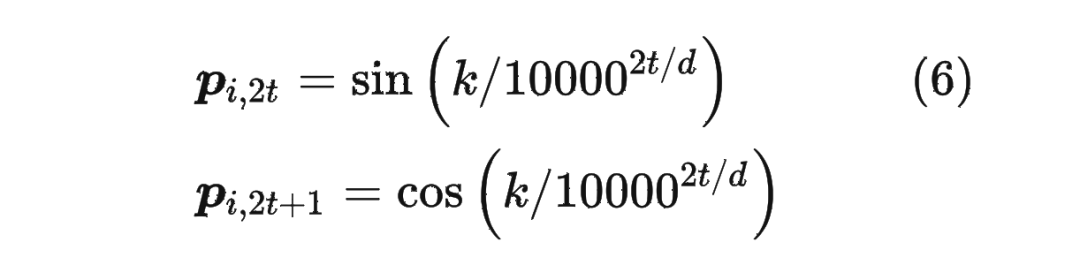
其中 表示位置 維度向量 中的第 位置分量也就是偶數(shù)索引位置的計(jì)算公式,而 就對(duì)應(yīng)第 位置分量也就是奇數(shù)索引位置的計(jì)算公式。
1.3 2維旋轉(zhuǎn)位置編碼
論文中提出為了能利用上 token 之間的相對(duì)位置信息,假定 query 向量 和 key 向量 之間的內(nèi)積操作可以被一個(gè)函數(shù) 表示,該函數(shù) 的輸入是詞嵌入向量 , 和它們之間的相對(duì)位置 :
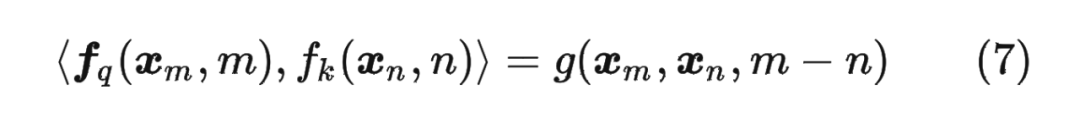 接下來(lái)的目標(biāo)就是找到一個(gè)等價(jià)的位置編碼方式,從而使得上述關(guān)系成立。
假定現(xiàn)在詞嵌入向量的維度是兩維 ,這樣就可以利用上 2 維度平面上的向量的幾何性質(zhì),然后論文中提出了一個(gè)滿足上述關(guān)系的 和 的形式如下:
接下來(lái)的目標(biāo)就是找到一個(gè)等價(jià)的位置編碼方式,從而使得上述關(guān)系成立。
假定現(xiàn)在詞嵌入向量的維度是兩維 ,這樣就可以利用上 2 維度平面上的向量的幾何性質(zhì),然后論文中提出了一個(gè)滿足上述關(guān)系的 和 的形式如下: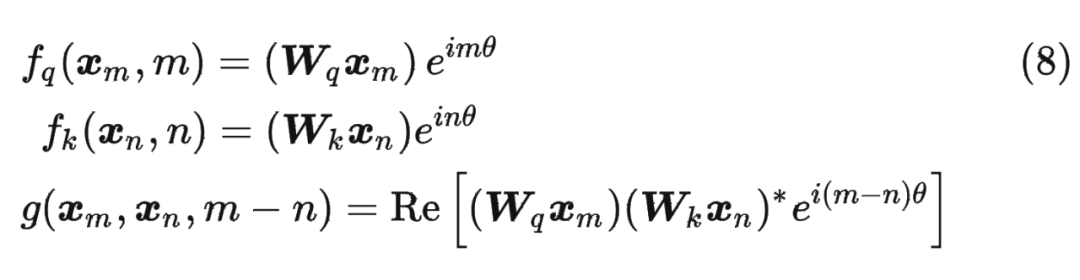 這里面 Re 表示復(fù)數(shù)的實(shí)部。
進(jìn)一步地, 可以表示成下面的式子:
這里面 Re 表示復(fù)數(shù)的實(shí)部。
進(jìn)一步地, 可以表示成下面的式子: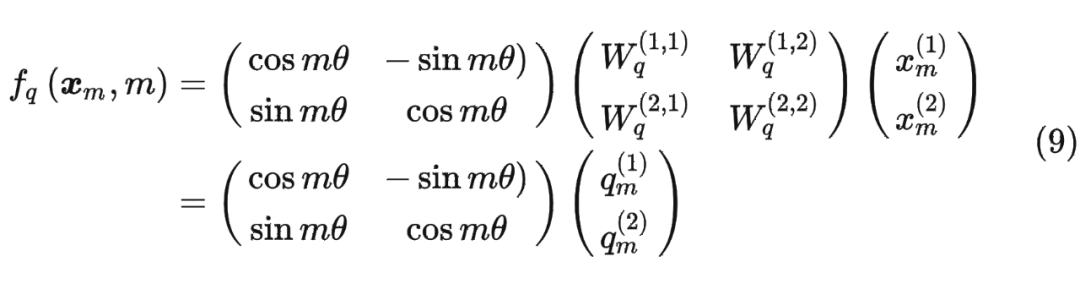 看到這里會(huì)發(fā)現(xiàn),這不就是 query 向量乘以了一個(gè)旋轉(zhuǎn)矩陣嗎?這就是為什么叫做旋轉(zhuǎn)位置編碼的原因。
同理, 可以表示成下面的式子:
看到這里會(huì)發(fā)現(xiàn),這不就是 query 向量乘以了一個(gè)旋轉(zhuǎn)矩陣嗎?這就是為什么叫做旋轉(zhuǎn)位置編碼的原因。
同理, 可以表示成下面的式子: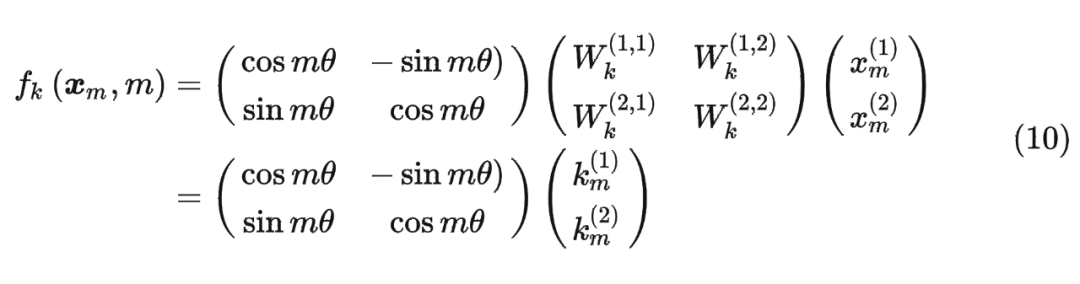 最終 可以表示如下:
最終 可以表示如下:
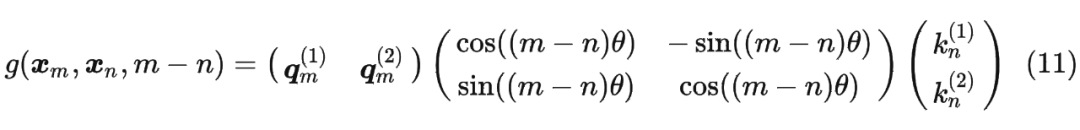
將2維推廣到任意維度,可以表示如下:
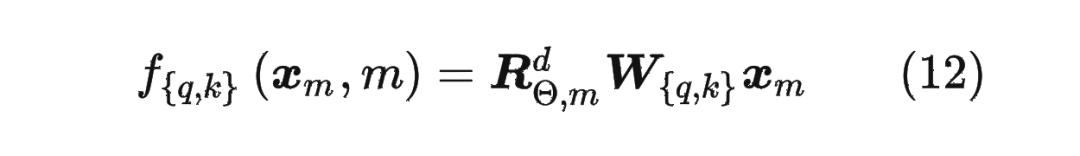 內(nèi)積滿足線性疊加性,因此任意偶數(shù)維的 RoPE,我們都可以表示為二維情形的拼接,即
內(nèi)積滿足線性疊加性,因此任意偶數(shù)維的 RoPE,我們都可以表示為二維情形的拼接,即 將 RoPE 應(yīng)用到前面公式(4)的 Self-Attention 計(jì)算,可以得到包含相對(duì)位置信息的 Self-Attetion:
將 RoPE 應(yīng)用到前面公式(4)的 Self-Attention 計(jì)算,可以得到包含相對(duì)位置信息的 Self-Attetion: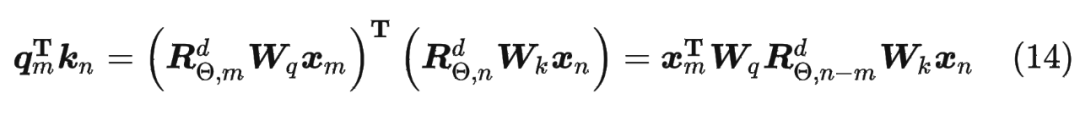
其中,。
值得指出的是,由于 是一個(gè)正交矩陣,它不會(huì)改變向量的模長(zhǎng),因此通常來(lái)說(shuō)它不會(huì)改變?cè)P偷姆€(wěn)定性。 1.5 RoPE 的高效計(jì)算由于 的稀疏性,所以直接用矩陣乘法來(lái)實(shí)現(xiàn)會(huì)很浪費(fèi)算力,推薦通過(guò)下述方式來(lái)實(shí)現(xiàn) RoPE:
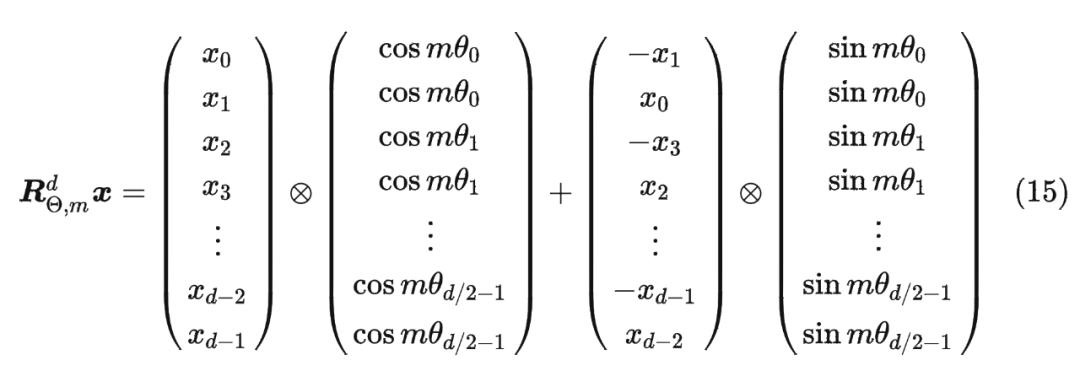
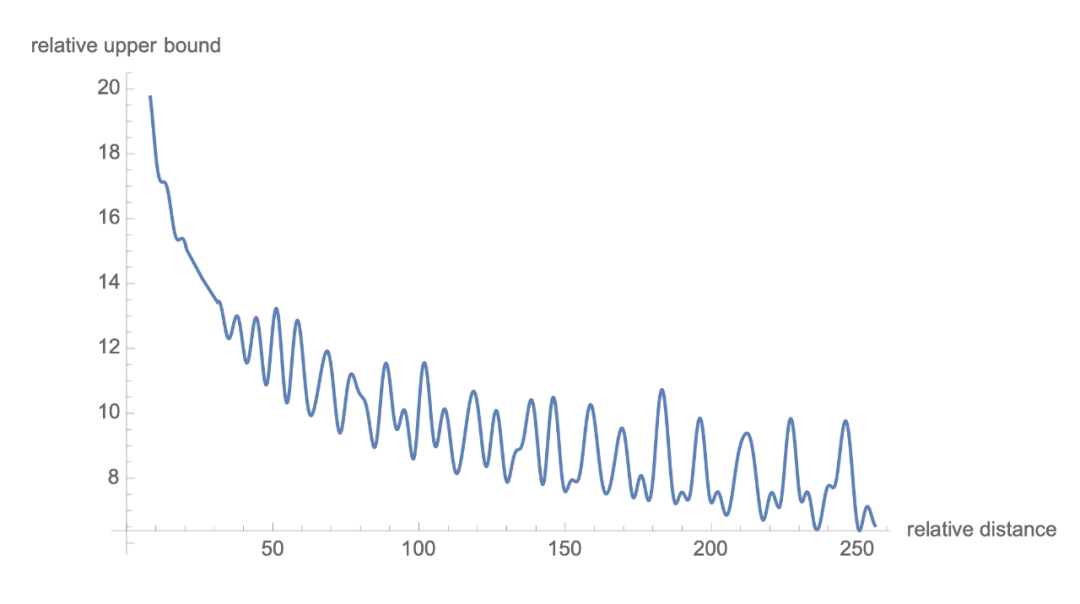
1.6 遠(yuǎn)程衰減
可以看到,RoPE 形式上和前面公式(6)Sinusoidal 位置編碼有點(diǎn)相似,只不過(guò) Sinusoidal 位置編碼是加性的,而 RoPE 可以視為乘性的。在 的選擇上,RoPE 同樣沿用了 Sinusoidal 位置編碼的方案,即 ,它可以帶來(lái)一定的遠(yuǎn)程衰減性。
具體證明如下:將 兩兩分組后,它們加上 RoPE 后的內(nèi)積可以用復(fù)數(shù)乘法表示為:
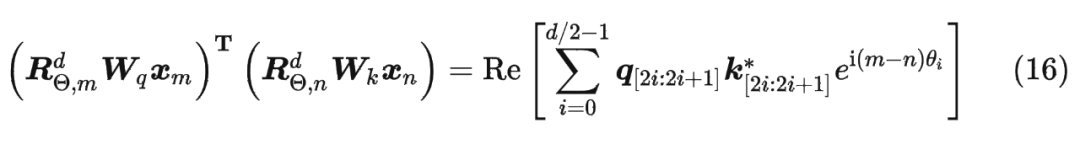
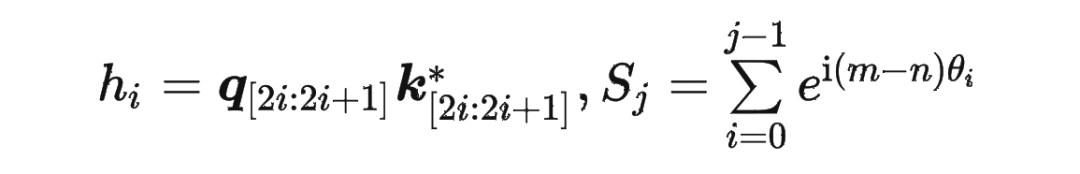
并約定 ,那么由 Abel 變換(分部求和法)可以得到:
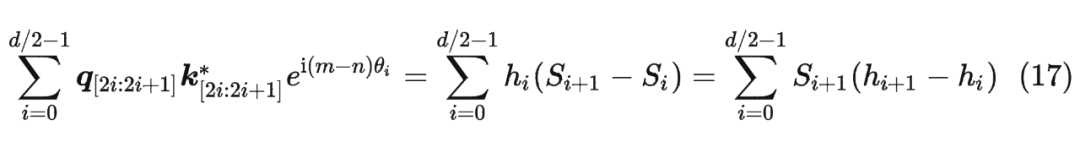
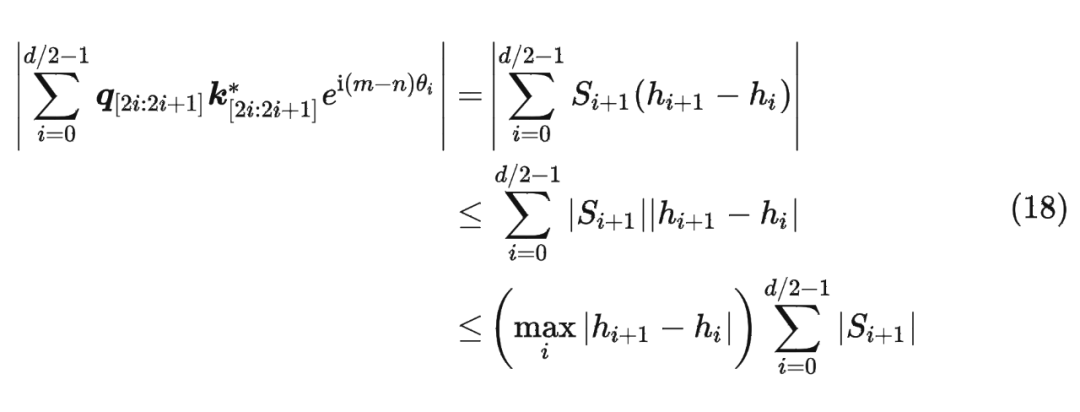
RoPE實(shí)驗(yàn)
我們看一下 RoPE 在預(yù)訓(xùn)練階段的實(shí)驗(yàn)效果:
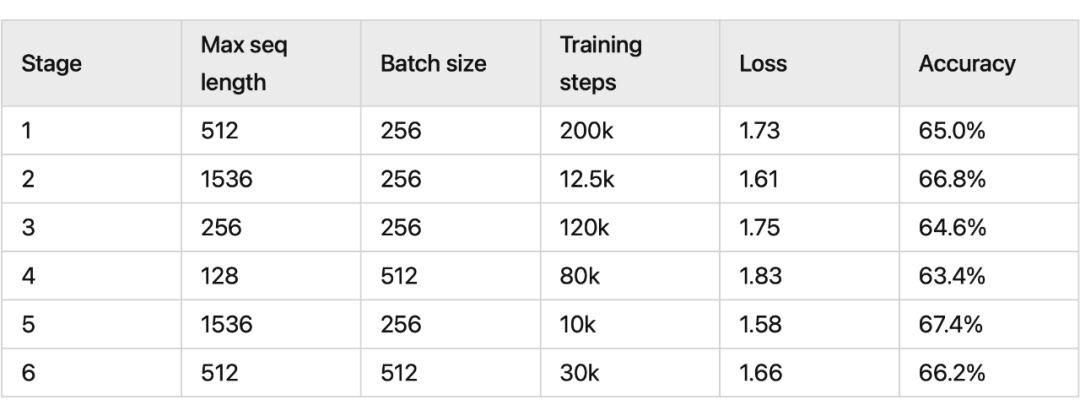
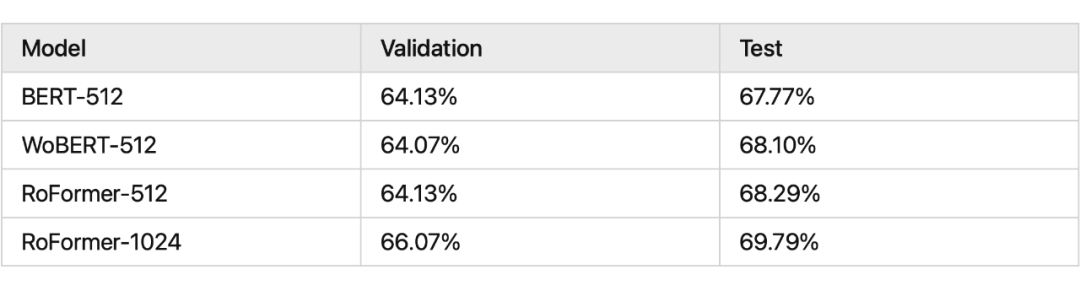 其中 RoFormer 是一個(gè)絕對(duì)位置編碼替換為 RoPE 的 WoBERT 模型,后面的參數(shù)(512)是微調(diào)時(shí)截?cái)嗟膍axlen,可以看到 RoPE 確實(shí)能較好地處理長(zhǎng)文本語(yǔ)義。
其中 RoFormer 是一個(gè)絕對(duì)位置編碼替換為 RoPE 的 WoBERT 模型,后面的參數(shù)(512)是微調(diào)時(shí)截?cái)嗟膍axlen,可以看到 RoPE 確實(shí)能較好地處理長(zhǎng)文本語(yǔ)義。
RoPE代碼實(shí)現(xiàn)
Meta 的 LLAMA 和 清華的 ChatGLM 都使用了 RoPE 編碼,下面看一下具體實(shí)現(xiàn)。
3.1 在LLAMA中的實(shí)現(xiàn)
#生成旋轉(zhuǎn)矩陣
defprecompute_freqs_cis(dim:int,seq_len:int,theta:float=10000.0):
#計(jì)算詞向量元素兩兩分組之后,每組元素對(duì)應(yīng)的旋轉(zhuǎn)角度 heta_i
freqs=1.0/(theta**(torch.arange(0,dim,2)[:(dim//2)].float()/dim))
#生成token序列索引t=[0,1,...,seq_len-1]
t=torch.arange(seq_len,device=freqs.device)
#freqs.shape=[seq_len,dim//2]
freqs=torch.outer(t,freqs).float()#計(jì)算m* heta
#計(jì)算結(jié)果是個(gè)復(fù)數(shù)向量
#假設(shè)freqs=[x,y]
#則freqs_cis=[cos(x)+sin(x)i,cos(y)+sin(y)i]
freqs_cis=torch.polar(torch.ones_like(freqs),freqs)
returnfreqs_cis
#旋轉(zhuǎn)位置編碼計(jì)算
defapply_rotary_emb(
xq:torch.Tensor,
xk:torch.Tensor,
freqs_cis:torch.Tensor,
)->Tuple[torch.Tensor,torch.Tensor]:
#xq.shape=[batch_size,seq_len,dim]
#xq_.shape=[batch_size,seq_len,dim//2,2]
xq_=xq.float().reshape(*xq.shape[:-1],-1,2)
xk_=xk.float().reshape(*xk.shape[:-1],-1,2)
#轉(zhuǎn)為復(fù)數(shù)域
xq_=torch.view_as_complex(xq_)
xk_=torch.view_as_complex(xk_)
#應(yīng)用旋轉(zhuǎn)操作,然后將結(jié)果轉(zhuǎn)回實(shí)數(shù)域
#xq_out.shape=[batch_size,seq_len,dim]
xq_out=torch.view_as_real(xq_*freqs_cis).flatten(2)
xk_out=torch.view_as_real(xk_*freqs_cis).flatten(2)
returnxq_out.type_as(xq),xk_out.type_as(xk)
classAttention(nn.Module):
def__init__(self,args:ModelArgs):
super().__init__()
self.wq=Linear(...)
self.wk=Linear(...)
self.wv=Linear(...)
self.freqs_cis=precompute_freqs_cis(dim,max_seq_len*2)
defforward(self,x:torch.Tensor):
bsz,seqlen,_=x.shape
xq,xk,xv=self.wq(x),self.wk(x),self.wv(x)
xq=xq.view(batch_size,seq_len,dim)
xk=xk.view(batch_size,seq_len,dim)
xv=xv.view(batch_size,seq_len,dim)
#attention操作之前,應(yīng)用旋轉(zhuǎn)位置編碼
xq,xk=apply_rotary_emb(xq,xk,freqs_cis=freqs_cis)
#scores.shape=(bs,seqlen,seqlen)
scores=torch.matmul(xq,xk.transpose(1,2))/math.sqrt(dim)
scores=F.softmax(scores.float(),dim=-1)
output=torch.matmul(scores,xv)#(batch_size,seq_len,dim)
#......
In[239]:freqs_cis
Out[239]:
tensor([[1.0000+0.0000j,1.0000+0.0000j,1.0000+0.0000j,1.0000+0.0000j],
[0.5403+0.8415j,0.9950+0.0998j,0.9999+0.0100j,1.0000+0.0010j],
[-0.4161+0.9093j,0.9801+0.1987j,0.9998+0.0200j,1.0000+0.0020j]])
以結(jié)果中的第二行為例(對(duì)應(yīng)的 m = 1),也就是:
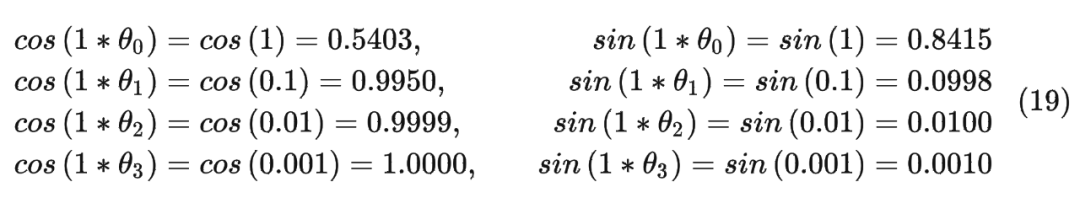 最終按照公式(12)可以得到編碼之后的 。
注意:在代碼中是直接用 freqs_cis[0] * xq_[0] 的結(jié)果表示第一個(gè) token 對(duì)應(yīng)的旋轉(zhuǎn)編碼(和公式 12 計(jì)算方式有所區(qū)別)。其中將原始的 query 向量 轉(zhuǎn)換為了復(fù)數(shù)形式。
最終按照公式(12)可以得到編碼之后的 。
注意:在代碼中是直接用 freqs_cis[0] * xq_[0] 的結(jié)果表示第一個(gè) token 對(duì)應(yīng)的旋轉(zhuǎn)編碼(和公式 12 計(jì)算方式有所區(qū)別)。其中將原始的 query 向量 轉(zhuǎn)換為了復(fù)數(shù)形式。
In[351]:q_=q.float().reshape(*q.shape[:-1],-1,2)
In[352]:q_[0]
Out[352]:
tensor([[[1.0247,0.4782],
[1.5593,0.2119],
[0.4175,0.5309],
[0.4858,0.1850]],
[[-1.7456,0.6849],
[0.3844,1.1492],
[0.1700,0.2106],
[0.5433,0.2261]],
[[-1.1206,0.6969],
[0.8371,-0.7765],
[-0.3076,0.1704],
[-0.5999,-1.7029]]])
In[353]:xq=torch.view_as_complex(q_)
In[354]:xq[0]
Out[354]:
tensor([[1.0247+0.4782j,1.5593+0.2119j,0.4175+0.5309j,0.4858+0.1850j],
[-1.7456+0.6849j,0.3844+1.1492j,0.1700+0.2106j,0.5433+0.2261j],
[-1.1206+0.6969j,0.8371-0.7765j,-0.3076+0.1704j,-0.5999-1.7029j]])
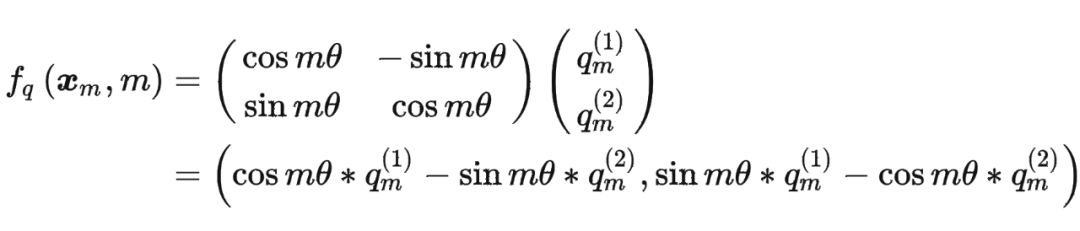
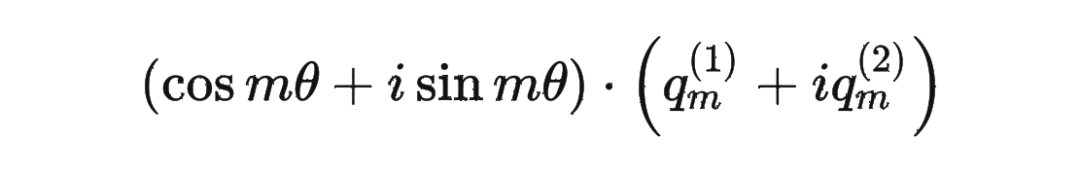
classRotaryEmbedding(torch.nn.Module):
def__init__(self,dim,base=10000,precision=torch.half,learnable=False):
super().__init__()
#計(jì)算 heta_i
inv_freq=1./(base**(torch.arange(0,dim,2).float()/dim))
inv_freq=inv_freq.half()
self.learnable=learnable
iflearnable:
self.inv_freq=torch.nn.Parameter(inv_freq)
self.max_seq_len_cached=None
else:
self.register_buffer('inv_freq',inv_freq)
self.max_seq_len_cached=None
self.cos_cached=None
self.sin_cached=None
self.precision=precision
defforward(self,x,seq_dim=1,seq_len=None):
ifseq_lenisNone:
seq_len=x.shape[seq_dim]
ifself.max_seq_len_cachedisNoneor(seq_len>self.max_seq_len_cached):
self.max_seq_len_cached=Noneifself.learnableelseseq_len
#生成token序列索引t=[0,1,...,seq_len-1]
t=torch.arange(seq_len,device=x.device,dtype=self.inv_freq.dtype)
#對(duì)應(yīng)m* heta
freqs=torch.einsum('i,j->ij',t,self.inv_freq)
#將m* heta拼接兩次,對(duì)應(yīng)復(fù)數(shù)的實(shí)部和虛部
emb=torch.cat((freqs,freqs),dim=-1).to(x.device)
ifself.precision==torch.bfloat16:
emb=emb.float()
#[sx,1(b*np),hn]
cos_cached=emb.cos()[:,None,:]#計(jì)算得到cos(m* heta)
sin_cached=emb.sin()[:,None,:]#計(jì)算得到cos(m* heta)
ifself.precision==torch.bfloat16:
cos_cached=cos_cached.bfloat16()
sin_cached=sin_cached.bfloat16()
ifself.learnable:
returncos_cached,sin_cached
self.cos_cached,self.sin_cached=cos_cached,sin_cached
returnself.cos_cached[:seq_len,...],self.sin_cached[:seq_len,...]
def_apply(self,fn):
ifself.cos_cachedisnotNone:
self.cos_cached=fn(self.cos_cached)
ifself.sin_cachedisnotNone:
self.sin_cached=fn(self.sin_cached)
returnsuper()._apply(fn)
defrotate_half(x):
x1,x2=x[...,:x.shape[-1]//2],x[...,x.shape[-1]//2:]
returntorch.cat((-x2,x1),dim=x1.ndim-1)
RoPE的外推性
我們都知道 RoPE 具有很好的外推性,前面的實(shí)驗(yàn)結(jié)果也證明了這一點(diǎn)。這里解釋下具體原因。 RoPE 可以通過(guò)旋轉(zhuǎn)矩陣來(lái)實(shí)現(xiàn)位置編碼的外推,即可以通過(guò)旋轉(zhuǎn)矩陣來(lái)生成超過(guò)預(yù)期訓(xùn)練長(zhǎng)度的位置編碼。這樣可以提高模型的泛化能力和魯棒性。 我們回顧一下 RoPE 的工作原理:假設(shè)我們有一個(gè) 維的絕對(duì)位置編碼 ,其中 是位置索引。我們可以將 看成一個(gè) 維空間中的一個(gè)點(diǎn)。我們可以定義一個(gè) 維空間中的一個(gè)旋轉(zhuǎn)矩陣 ,它可以將任意一個(gè)點(diǎn)沿著某個(gè)軸旋轉(zhuǎn)一定的角度。我們可以用 來(lái)變換 ,得到一個(gè)新的點(diǎn) 。我們可以發(fā)現(xiàn), 和 的距離是相等的,即 。這意味著 和 的相對(duì)關(guān)系沒(méi)有改變。但是, 和 的距離可能發(fā)生改變,即 。這意味著 和 的相對(duì)關(guān)系有所改變。因此,我們可以用 來(lái)調(diào)整不同位置之間的相對(duì)關(guān)系。 如果我們想要生成超過(guò)預(yù)訓(xùn)練長(zhǎng)度的位置編碼,我們只需要用 來(lái)重復(fù)變換最后一個(gè)預(yù)訓(xùn)練位置編碼 ,得到新的位置編碼
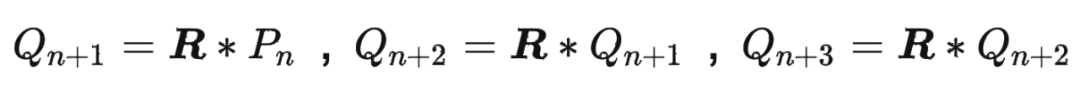 依此類推。這樣就可以得到任意長(zhǎng)度的位置編碼序列 ,其中 可以大于 。由于 是一個(gè)正交矩陣,它保證了 和 的距離不會(huì)無(wú)限增大或縮小,而是在一個(gè)有限范圍內(nèi)波動(dòng)。這樣就可以避免數(shù)值溢出或下溢的問(wèn)題。同時(shí),由于 是一個(gè)可逆矩陣,它保證了 和 的距離可以通過(guò) 的逆矩陣 還原到 和 的距離,即
依此類推。這樣就可以得到任意長(zhǎng)度的位置編碼序列 ,其中 可以大于 。由于 是一個(gè)正交矩陣,它保證了 和 的距離不會(huì)無(wú)限增大或縮小,而是在一個(gè)有限范圍內(nèi)波動(dòng)。這樣就可以避免數(shù)值溢出或下溢的問(wèn)題。同時(shí),由于 是一個(gè)可逆矩陣,它保證了 和 的距離可以通過(guò) 的逆矩陣 還原到 和 的距離,即
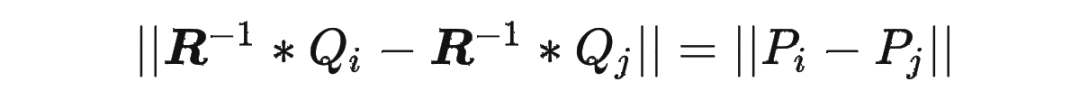
總結(jié)
最近一直聽到旋轉(zhuǎn)編碼這個(gè)詞,但是一直沒(méi)有仔細(xì)看具體原理。今天花時(shí)間仔細(xì)看了一遍,確實(shí)理論寫的比較完備,而且實(shí)驗(yàn)效果也不錯(cuò)。目前很多的大模型,都選擇了使用了這種編碼方式(LLAMA、GLM 等)。
附錄
這里補(bǔ)充一下前面公式 1.3.2 節(jié)中,公式(8)~(11)是怎么推導(dǎo)出來(lái)的。 回到之前的公式(8),編碼之后的 以及內(nèi)積 的形式如下:
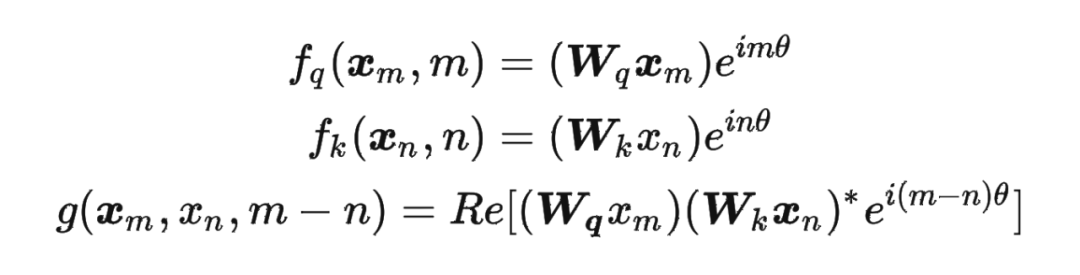
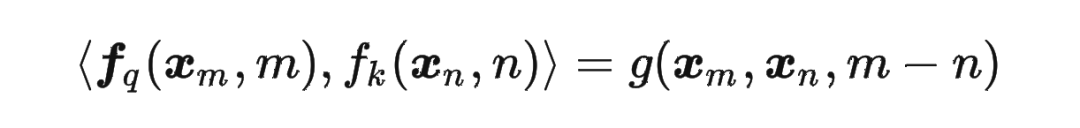
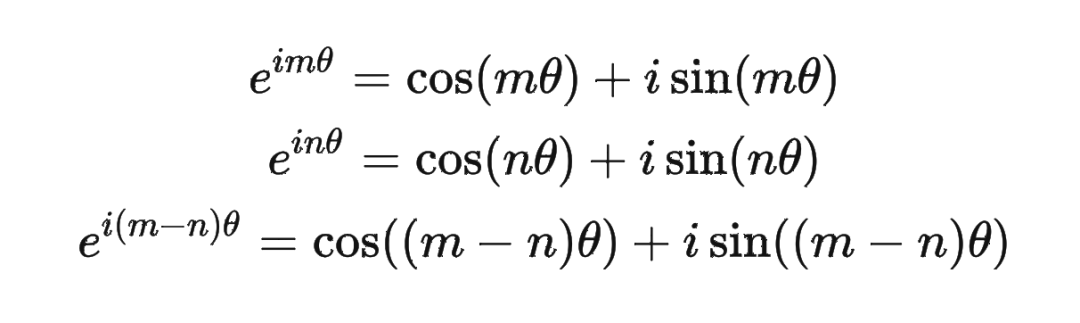 然后我們看回公式:
然后我們看回公式: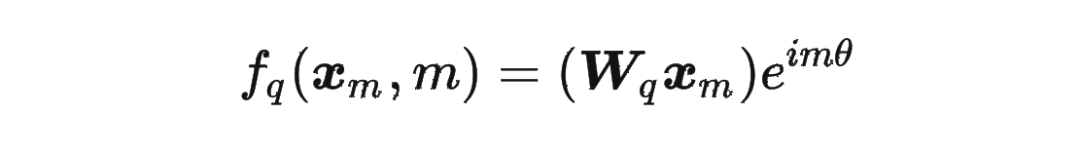 其中 是個(gè)二維矩陣, 是個(gè)二維向量,相乘的結(jié)果也是一個(gè)二維向量,這里用 表示:
其中 是個(gè)二維矩陣, 是個(gè)二維向量,相乘的結(jié)果也是一個(gè)二維向量,這里用 表示:
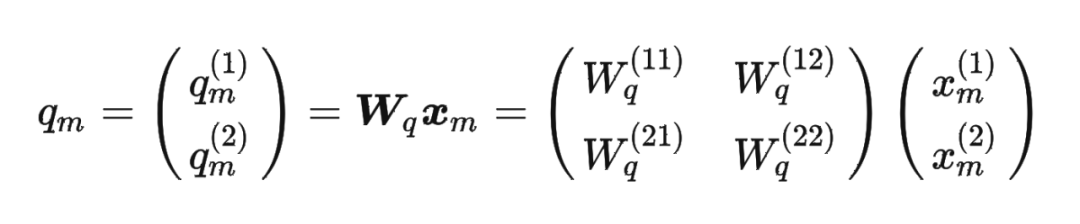
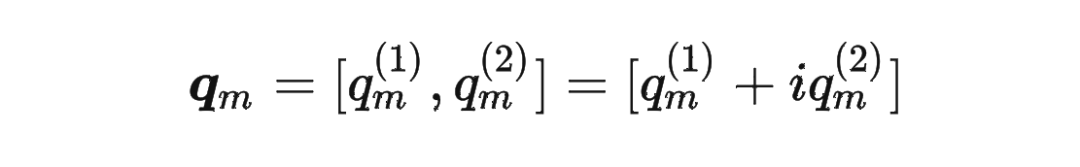 接著
接著
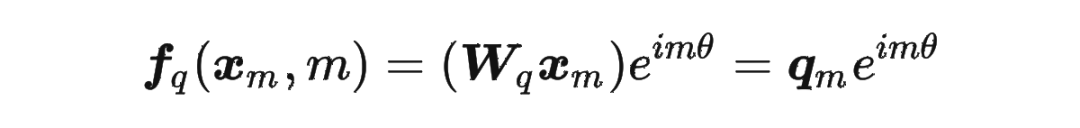
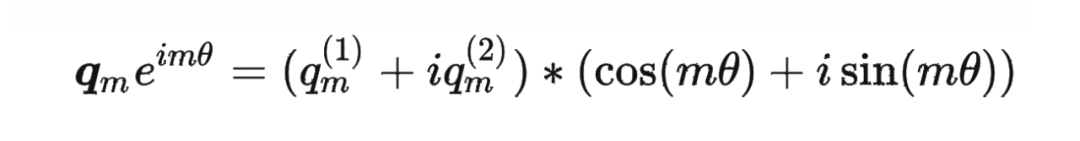
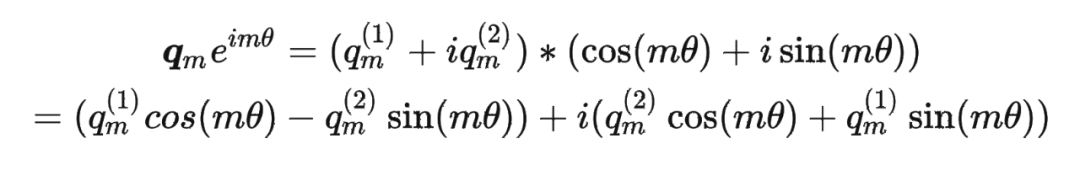
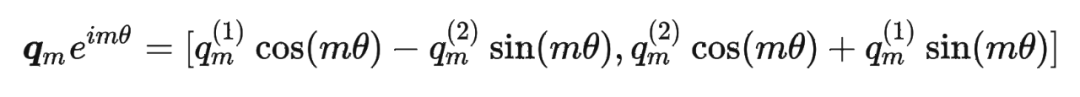
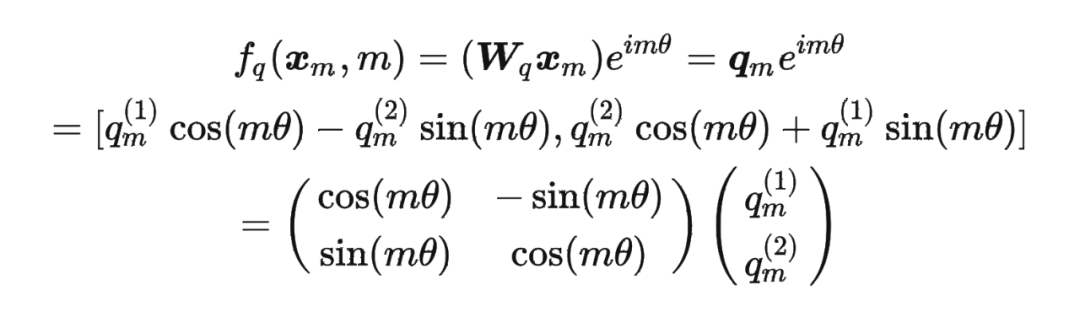
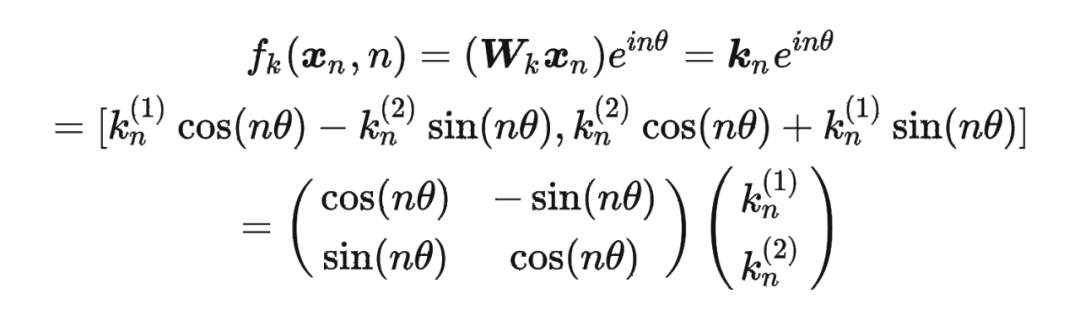
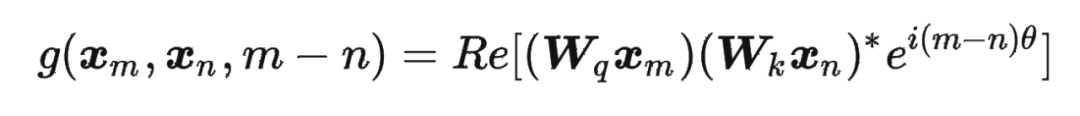 其中 表示一個(gè)復(fù)數(shù) 的實(shí)部部分,而 則表示復(fù)數(shù) 的共軛。
復(fù)習(xí)一下共軛復(fù)數(shù)的定義:
其中 表示一個(gè)復(fù)數(shù) 的實(shí)部部分,而 則表示復(fù)數(shù) 的共軛。
復(fù)習(xí)一下共軛復(fù)數(shù)的定義:
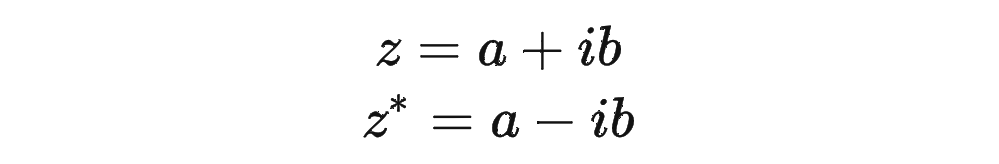
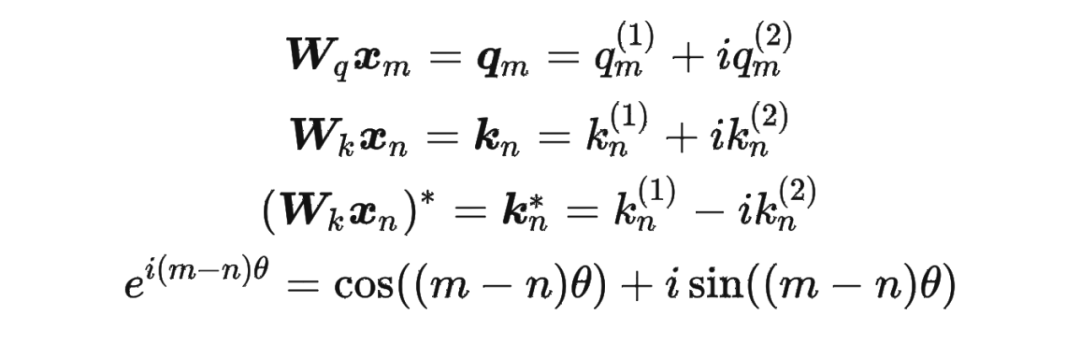
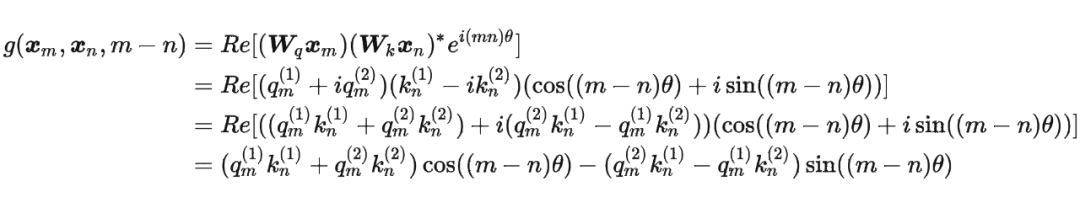
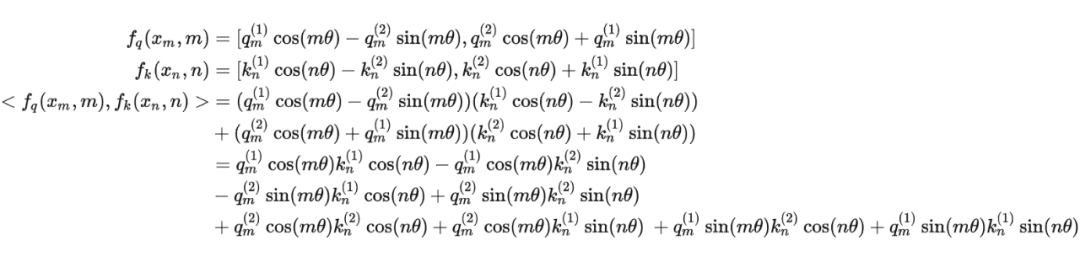
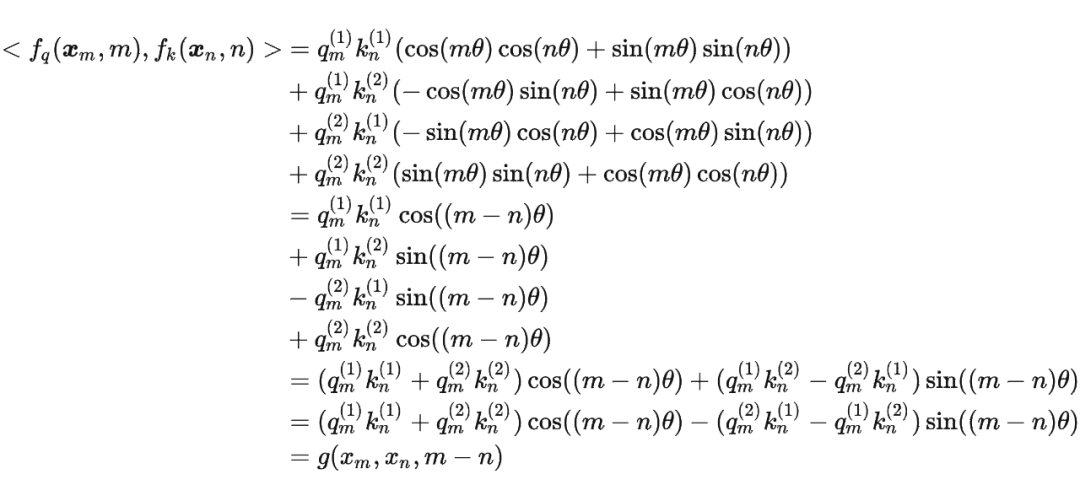
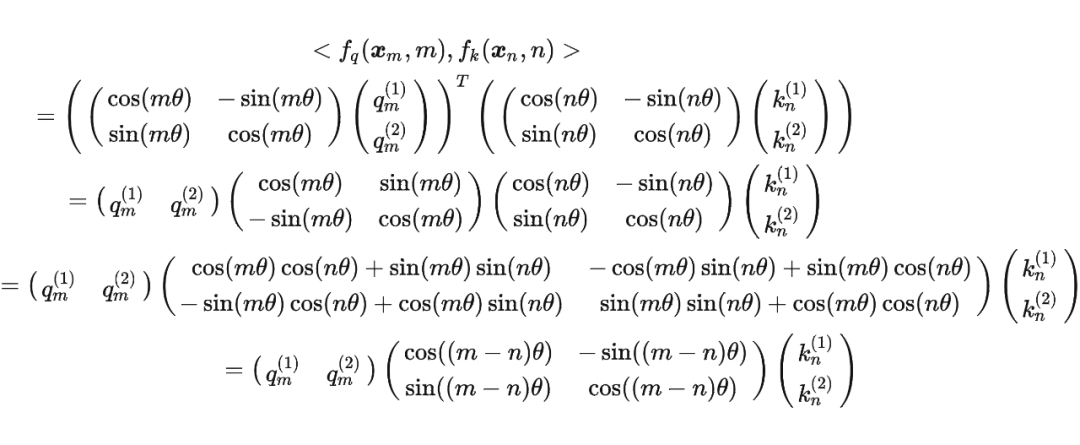 ?
?
-
向量
+關(guān)注
關(guān)注
0文章
55瀏覽量
11829 -
旋轉(zhuǎn)編碼
+關(guān)注
關(guān)注
0文章
6瀏覽量
10550 -
大模型
+關(guān)注
關(guān)注
2文章
2962瀏覽量
3715
原文標(biāo)題:十分鐘讀懂旋轉(zhuǎn)編碼(RoPE)
文章出處:【微信號(hào):zenRRan,微信公眾號(hào):深度學(xué)習(xí)自然語(yǔ)言處理】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
快充技術(shù)&芯片詳解 十分鐘讓你的手機(jī)滿血復(fù)活
十分鐘學(xué)會(huì)Xilinx FPGA 設(shè)計(jì)1.1
ModelSim SE 十分鐘入門
全球首發(fā)十分鐘快速充滿電移動(dòng)電源
采集系統(tǒng)需要隔十分鐘采集10S數(shù)據(jù),怎么實(shí)現(xiàn)?
基于STM32F103RB的數(shù)碼管如何去實(shí)現(xiàn)十分鐘計(jì)時(shí)呢
遇到SE5經(jīng)常自動(dòng)重啟,大約十幾分鐘到二十分鐘左右重啟一次的問(wèn)題如何解決?
十分鐘學(xué)會(huì)Xilinx FPGA 設(shè)計(jì)
三星改革智能手機(jī)充電技術(shù),充滿只需十分鐘
英國(guó)搭建太陽(yáng)能汽車充電網(wǎng)試點(diǎn)項(xiàng)目,電動(dòng)汽車在三十分鐘內(nèi)完成充電
十分鐘分析穩(wěn)壓三極管工作原理資料下載



















評(píng)論