運算放大器(簡稱運放)的發明使得電子技術進入了“運算”時代,直接促使了電子計算機的誕生,它也因此而得名“運算放大器”。我們先來看看常見的運放“核心”是怎么樣的。
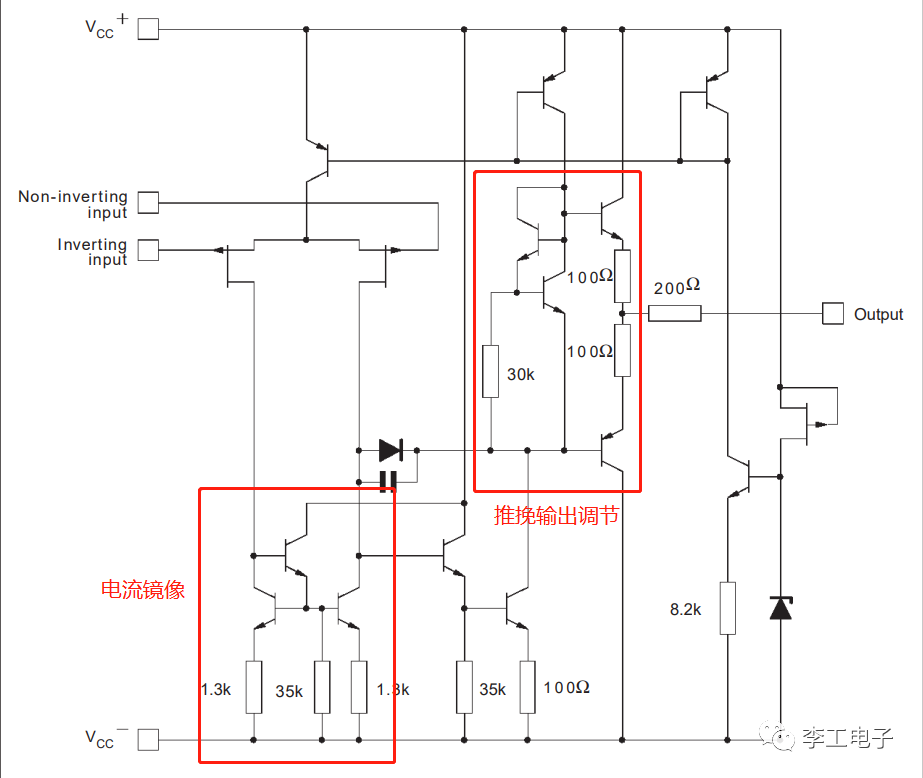
在閉環的結構當中,運放內部的鏡像電路總是企圖維持兩端電流的平衡,一旦失衡,它就會通過調節輸出端(output)的電流形態,進一步通過反饋環路來檢測輸入(input)兩端的狀態,直到出現新的平衡,此時的運放就得到一個穩定的輸出狀態 。我們可以根據這個原理來分析運放的經典應用電路。
緩沖器的配置
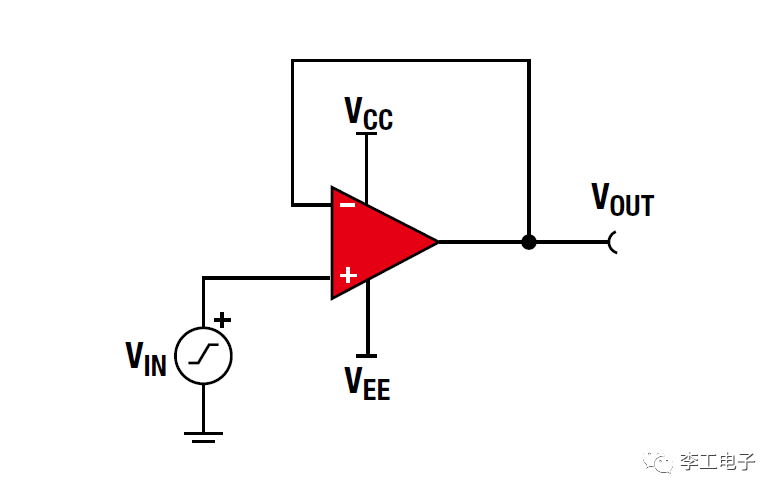
這是一個經典的緩沖器方案,也可以稱作電壓跟隨器(輸出電流的能力與運放內部的輸出結構有關)。我們根據上述的鏡像原理, 運放輸入兩端的電壓可以看成是相等的(嚴格來說是動態平衡) ,因此我們可以直接得出Vin=Vout的結論。
同相與反相
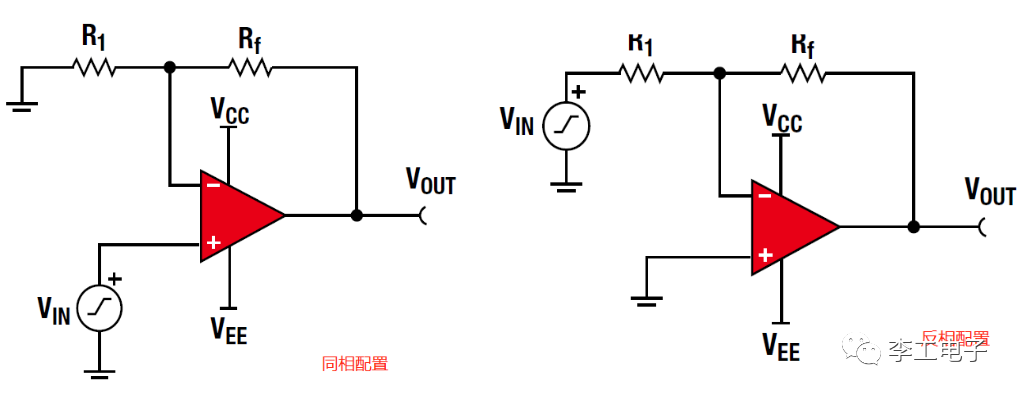
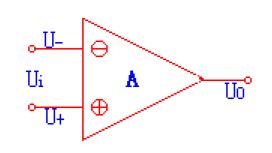
先來看同相的配置,由于在反饋環路中增加了電阻分壓器,可以精準地控制返回到輸入端的電壓值。因此可以得出增益的計算公式G=Rf/R1+1;同理可以得出反相配置的增益G=-Rf/R1。 **這里的“同相”指的是信號源接運放的正端,與輸出信號的相位相同;“反相”是指信號源接運放的負端,與輸出信號的相位相反** 。
加法器配置
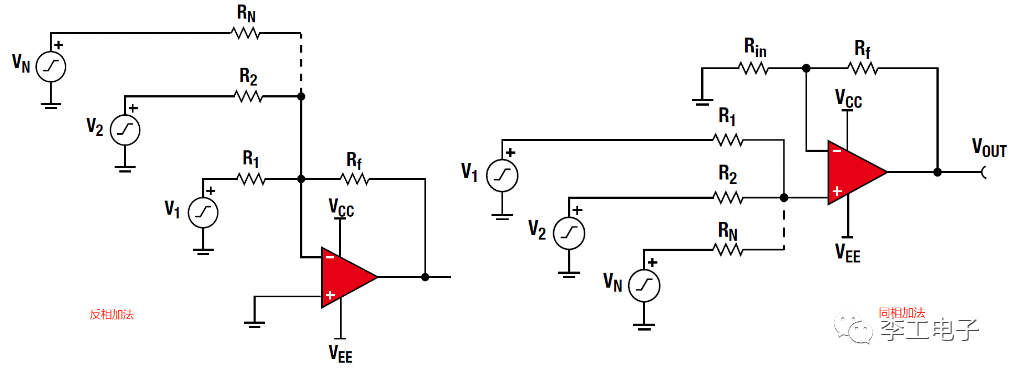
明白了單路同相與反相的配置原理,對于多路的信號輸入,我們可以直接按照加法來計算,“加法器”的稱謂由此而來。先看反相加法的配置,把多路信號疊加起來就變成:
Vout=-Rf(V1/R1+V2/R2+...+Vn/Rn) ;
此時如果R1=R2=...=Rn,則:
Vout=-Rf(V1+V2+...+Vn)/R1 ;
再來看同相加法配置,
假設R1=R2=...=Rn,同理可得:
Vout=(Rf/Rin+1)(V1/N+V2/N+...+Vn/N) ,
其中N=輸入電阻器的數量。
以上就是通過運算放大器的基本原理衍生出的應用,無論是多復雜的電路,都離不開這些基本規則,簡單說就是反饋形式的變種,由此賦予了運放具備多種形式的“運算”功能。
-
放大器
+關注
關注
145文章
14132瀏覽量
216849 -
電阻器
+關注
關注
21文章
4044瀏覽量
63415 -
運算放大器
+關注
關注
217文章
5698瀏覽量
176371 -
緩沖器
+關注
關注
6文章
2042瀏覽量
46910 -
電壓跟隨器
+關注
關注
10文章
213瀏覽量
33179 -
電阻分壓器
+關注
關注
0文章
54瀏覽量
9734
發布評論請先 登錄
什么是運放?運算放大器的電壓傳輸特性
集成運算放大器芯片介紹
運算放大器的類型總結看這篇就夠了!(文末有驚喜)
運算放大器的原理和應用
集成運算放大器的選擇策略與應用技術
運算放大器和專用放大器的基礎教程
電子元器件基礎教程之運算放大器和功率放大器



















評論