摘要：給出了理想光具組系統矩陣的MATLAB計算程序，并借助MATLAB進行光線追跡與數值擬合，得到了像差(球差)的多項式及曲線圖。

0.引 言

幾何光學把光源或物體看成是由許多幾何點組成，并把由這種點發出的光抽象成幾何線一樣的光線，那么，只要討論光線的傳播來研究這種點經光學系統的成像，問題就變得非常簡便和實用。盡管幾何光學所研究的只是一種對真實情況的近似處理方法，按此方法所解決的有關光學系統的成像分析、計算和設計等方面的光學技術問題，在大多數場合下與實際情況相符。所以，幾何光學有很大的實用意義，是研究光學儀器理論必不可少的基礎。MATLAB作為一款優秀的數學軟件，集成了最優秀的算法，除具有強大的矩陣計算功能和友好的界面，還具備了良好的可視化性能．這些特點使得 MU蛆在光線計算、像差分析中大顯身手。

1.理想光具組的矩陣計算

幾何光學定律只在一級近似條件(sinφ≈φ)下成立，根據費馬定理在近軸條件下推出的物象方程，進而得到牛頓公式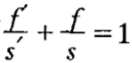（），高斯公式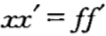（）以及光焦度公式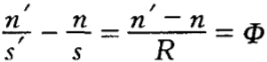（），使得宏觀光 學的問題基本解決。對于較復雜的光學系統，可以通 過追跡光線，根據物象相對性原理及逐個球面成像法，求出物體經整個系統后所成的像。由于近軸物象空間的光線狀態的變化可以描述成某種線性關系，因此，用矩陣方法處理許多折射面組成的復雜光學系統尤其便利，只要追隨光線寫下光線的傳遞矩陣及折射矩陣，再依次相乘，就可求出光學系統的基點和基面，也可得到物象關系。見表1

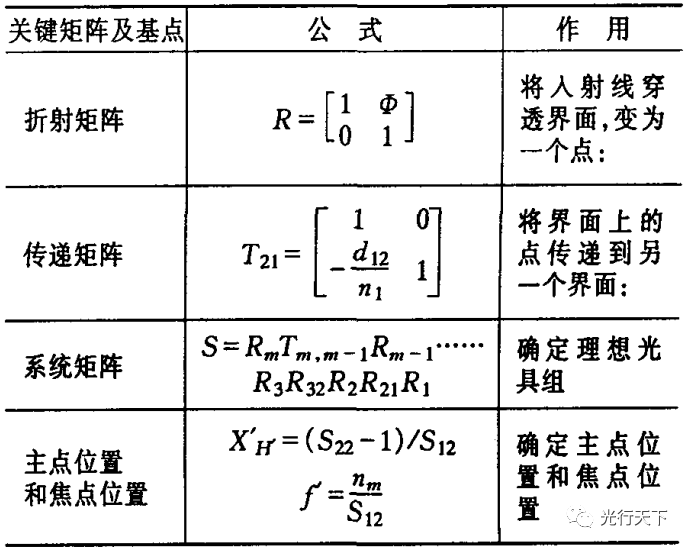
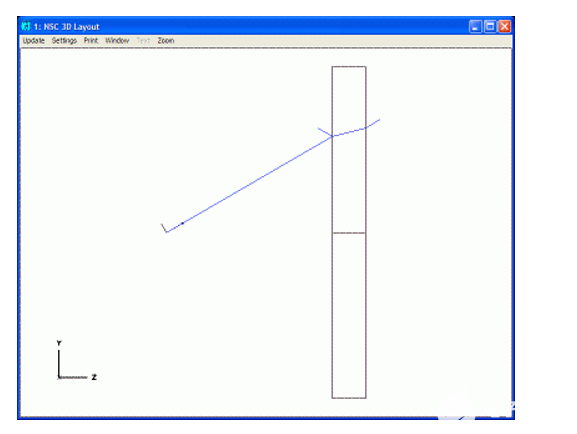
下面，以雙膠合望遠鏡的目鏡為例(如圖1所示)，

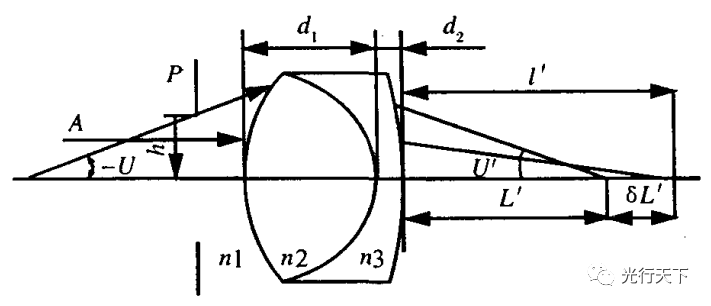
圖1.雙膠合透鏡目鏡球差示意光路圖

作有關系統矩陣的計算，rl=62.5，r2=-43.65，

r3=-124.35，nl=1，n2=1.51633，n3=1.6727，dl=4.0，d2=2.5，入射孔徑半徑a=10。

通過MATLAB編寫的程序，很容易得到S矩陣=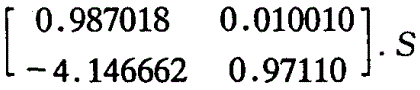矩陣計算程序流程如圖2所示。

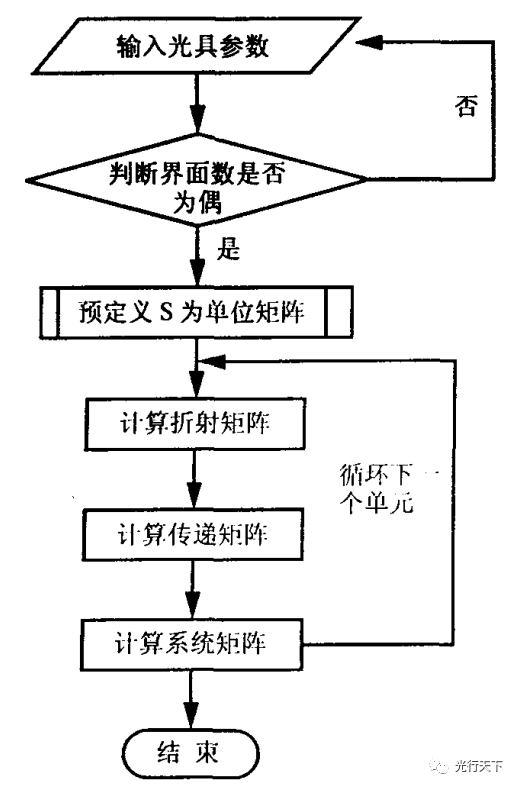
圖2. 系統矩陣計算程序流程圖

2.像差分析及可視化

我們已經知道，任何實際光學系統只要在近軸區，就能象理想光具系統那樣具完善成像的性質。因此，即使單個透鏡，只要其相對孔徑(孔徑僬距)和視場很小，也是能夠以單色光成完善像。但是，遺憾的是，只能對近軸小物體以細光束成完善像的光學系統并無實際意義，因為恰恰是相對孔徑和視場這兩個參數與光學系統的功能和使用價值密切相關。實際上，任何光學系統都需根據儀器的要求而具一定大小的視場和孔徑，它遠遠超出近軸區所限定的范圍。物面上各點成像光線的實際光路過于偏離理想路徑，是理想成像所應有的物象之間的共軛關系遭到破壞，形成像差。因此，任何實用的光學系統，旨在校正其像差以達到良好的成像質量，都需要反復做大量的光路計算。

仍以雙膠合望遠鏡的目鏡為例，以單色光的軸上點球差為對象，用MATLAB計算并分析像差。當透鏡孔徑較大時，光軸上某一點發出的光束經透鏡不再交于一點，這種現象稱為球差。對單色光而言，軸上點成像的不完善僅由球差引起(見球差示意光路)。由于像方截距L'是U或h的函數，則球差也必然是U或h的函數。但是L'與U或h之間被一套包括系統結構參數在內的光路計算公式所聯系，無法把球差用U或h顯函數形式表達出來。不過，可算出少數幾條實際光線后，用最小二乘法擬合出U或h多項式函數。由于光束對光軸的對稱性質，δL'的多項式中只能包含U或h的偶次方項，并且，只要計算子午面內的子午光線。可按下列公式組計算。

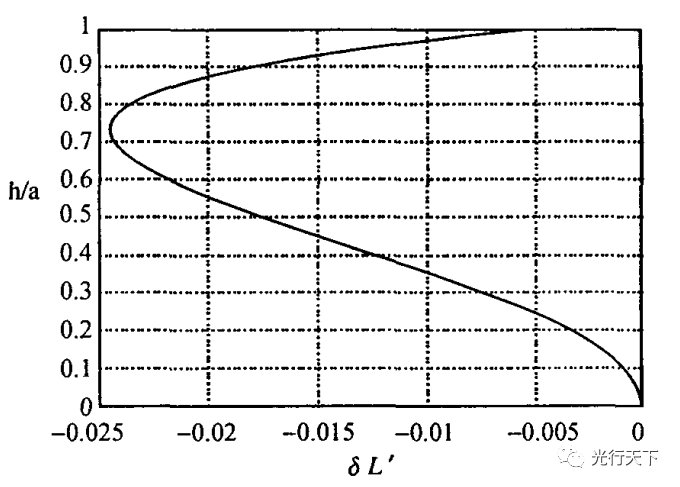
圖3.球差一光線高度曲線圖

4.結束語

借助腳LAB強大的矩陣計算功能，優秀的數值處理算法以及方便快捷的圖形可視化特點，來解決幾何光學中的理想光具組計算及像差分析，應該是一種有效的工具。

審核編輯：湯梓紅