傅里葉變換(Fourier Transform)是一種數學工具,用于將一個函數(通常是時間域函數)轉換成另一個函數(通常是頻域函數),以分析該函數的頻率特性。傅里葉變換是工程、物理學、計算機科學、圖像處理、音頻信號處理以及量子物理等多個領域中常用的一種數學方法。
時間域和頻域是信號或函數的兩種不同表示方式,它們包含的是同樣的信息,只是從不同的角度進行展示。傅里葉變換(Fourier Transform)和其逆變換(Inverse Fourier Transform)是從時間域到頻域、以及從頻域到時間域進行轉換的數學工具。
通過傅里葉分析,你可以將一個時間域函數轉換到頻域來分析它,或者將一個頻域函數轉回時間域以重構它。這兩種表示方式各有其優點和應用場景。例如,在信號處理、通信、圖像處理等多個領域,頻域分析提供了很多方便和高效的方法。
時間域函數
在時間域 (Time Domain) 中,信號或函數是按照時間變量 (通常表示為 t ) 來描述的。在這個表示中,你可以看到信號是如何隨著時間變化的。時間域表示是直觀的,因為它正是我們在現實世界中觀察信號的方式。例如,聲音波、電信號等都可以在時間域中表示。舉個簡單的例子,正弦波 Asin?(2πωt+?) 是一個時間域函數,其中 A 是振幅, ω 是頻率, ? 是相位角, t 是時間。
頻域函數
頻域(Frequency Domain)表示則是關注信號各個不同頻率成分的強度或相位。在頻域表示中,信號被表達為一系列正弦和余弦波的組合,這些正弦和余弦波有不同的頻率和振幅。這樣的表示使得我們能更容易地分析和理解信號的頻率特性。例如,傅里葉變換是一種常用的從時間域到頻域的轉換方法。在該變換后,將得到一個頻域函數,通常表示為 F(f) 或 F(ω) ,其中 f 或 ω 是頻率或角頻率。
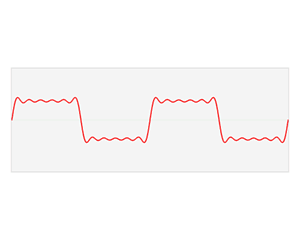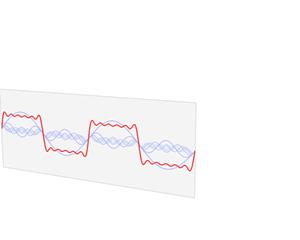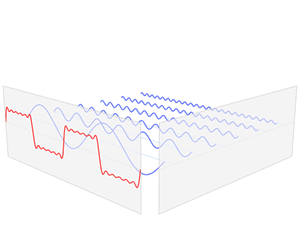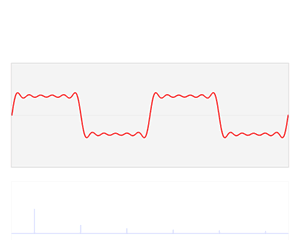
我們知道,任何周期函數在滿足狄利克雷條件下 (連續或只有有限個間斷點,且都是第一類間斷點;只有有限個極值點),都可以展開成一組正交函數的無窮級數之和。使用三角函數集的周期函數展開就是傅里葉級數。對于周期為 T 的信號 f(t) ,可以用三角函數集的線性組合來表示,即
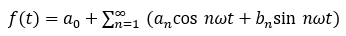
式中 ω=2π/T 是周期信號的角頻率,也成基波頻率, nω 稱為 n 次諧波頻率; 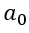 為信號的直流分量,
為信號的直流分量,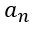 和
和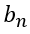 分別是余弦分量和正弦分量幅度。根據級數理論,傅里葉系數
分別是余弦分量和正弦分量幅度。根據級數理論,傅里葉系數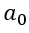 、
、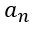 、
、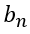 的計算公式為:
的計算公式為:
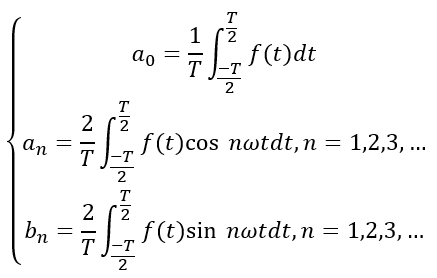
若將式子中同頻率的正弦項和余弦項合并,得到另一種形式的周期信號的傅里葉級數,即
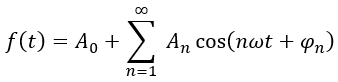
其中,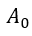 為信號的直流分量;
為信號的直流分量;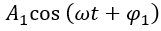 為信號的基頻分量,簡稱基波;
為信號的基頻分量,簡稱基波;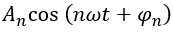 為信號的 n 次諧波, n 比較大的諧波,稱為高次諧波。上式說明任何周 期信號只要滿足狄利克雷條件,都可以分解成直流分量和一系列諧波分量之和,這些諧波分量的頻率是周期信號基頻的整數倍。比較兩種三角函數形式的傅里葉級數,可以看出它們的系數有如下關系:
為信號的 n 次諧波, n 比較大的諧波,稱為高次諧波。上式說明任何周 期信號只要滿足狄利克雷條件,都可以分解成直流分量和一系列諧波分量之和,這些諧波分量的頻率是周期信號基頻的整數倍。比較兩種三角函數形式的傅里葉級數,可以看出它們的系數有如下關系:
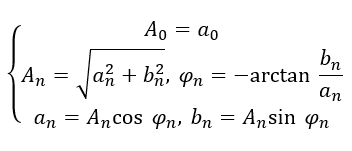
傅里葉變換適用于非周期性函數,將一個時間域函數轉換為其對應的頻域函數。可以將傅里葉級數看作是傅里葉變換的一個特殊情況。考慮一個周期為 T 的函數。如果 T 趨于無窮,這意味著函數是非周期性的,此時傅里葉級數會趨向于傅里葉變換。
連續傅里葉變換
對于連續函數 f(t) ,其連續傅里葉變換定義為:
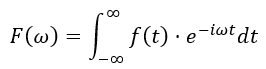
逆變換是:

離散傅里葉變換
對于離散信號,有離散傅里葉變換 (DFT) :
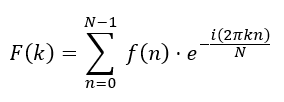
其逆變換是:
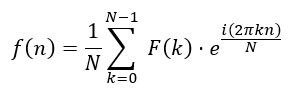
離散傅里葉變換在多項式乘法中的應用
對于n-1階多項式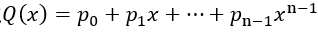 可以用n個點唯一表示(復數的點也是可以的)。令
可以用n個點唯一表示(復數的點也是可以的)。令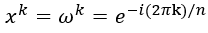 ,
,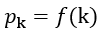 ,k=1,…,n-1
,k=1,…,n-1

只要我們可以求出矩陣的逆,就能反推出這個 Q 的系數。這個矩陣的逆的形式:
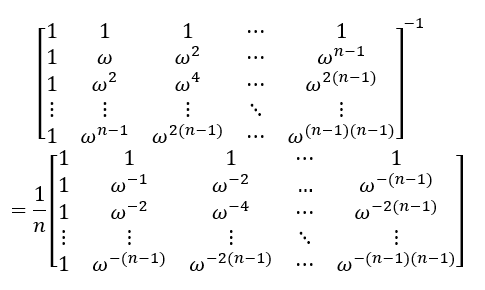
快速傅里葉變換(Fast Fourier Transform,簡稱FFT)是離散傅里葉變換(Discrete Fourier Transform,簡稱DFT)的一種高效算法。FFT能在 O(NlogN) 的時間復雜度內完成這一變換,而直接計算 DFT需要 O(N^2^) 的時間復雜度。
FFT基于一種名為“分治法”的遞歸策略,它將一個大問題分解為幾個更小的子問題來解決。對于一個 N 點的DFT,FFT會把它分成兩個 N/2 點的DFT,并遞歸地進行這個過程。
具體來說,FFT算法采用以下步驟:
- 分解階段:原始 N 點DFT分解為兩個 N/2 點的子序列,一個包含所有的偶數索引,另一個包含所有的奇數索引。
- 遞歸階段: 對這兩個 N/2 點子序列遞歸地應用FFT。
- 組合階段:使用遞歸解的結果,通過一系列的復數乘法和加法,組合得到原始N點DFT的結果。
原始的DFT定義為:
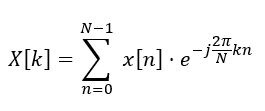
在FFT中,這個和會被分成兩部分:一部分是偶數索引,另一部分是奇數索引:
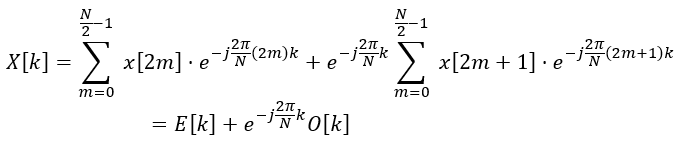
其中 E[k] 和 O[k] 是偶數和奇數序列的DFT。
具體例子
假設我們有一個 4 點的序列 x=[0,1,2,3] 。
- 分解
偶數序列 e=[0,2]
奇數序列 o=[1,3]
- 遞歸求解
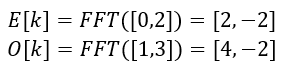
- 合并
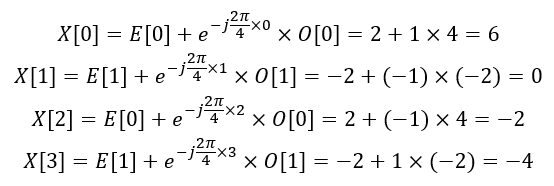
所以 X=[6,0,-2,-4] ,這就是序列 x 的DFT。這個過程大大減少了計算量,當 N 是2 的冪時,效率最高。
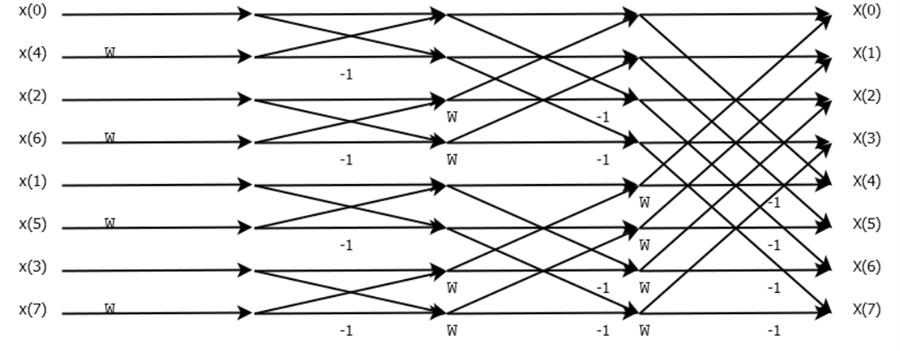
我們總結一下該過程的時間復雜度如下:
- DFT階段: 將兩個 n 度的多項式 A(x) 和 B(x) 使用FFT轉換到點值表示,分別得到 A(k) 和 B(k) 。時間復雜度為 2×O(nlogn)=O(nlogn) 。
- 乘法階段:在點值表示下,將 A(k) 和 B(k) 對應點值相乘得到 C(k) 。這是個 O(n) 時間復雜度的操作。
- IDFT階段:再次使用FFT (實際上是其逆變換IDFT)將 C(k) 轉換回系數表示得到 C(x) , 即 A(x)×B(x) 。時間復雜度是 O(nlogn) 。綜合這三個階段,總時間復雜度為 O(nlogn)+O(n)+O(nlogn)=O(nlogn) 。
數論變換(NTT)是有限域上離散傅里葉變化的一個變體。由于離散傅里葉變換是基于復數域上的變換,大多是浮點運算,故存在著一定的精度和效率問題。在許多應用中,需要對整數商環上的多項式進行變換,在這種情況下離散傅里葉變換的性能無法滿足要求。而NTT直接對整數進行處理而無需考慮浮點數中的存儲問題和精度問題,避免了浮點計算,大大提高了運算效率,非常適合基于LWE或RLWE難題的密碼系統。
數論變換(NTT)是整數環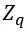 上定義的線性正交變換。設x(i),X(k)∈
上定義的線性正交變換。設x(i),X(k)∈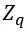 ,i=0,1,2…,n-1,k=0,1,2,…,n-1,有如下公式:
,i=0,1,2…,n-1,k=0,1,2,…,n-1,有如下公式:
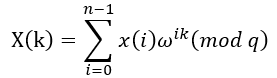
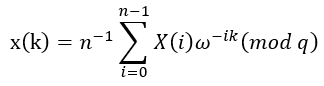
公式中ω為模q的n次單位原根,滿足
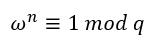
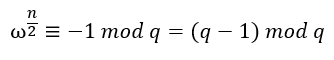
n為整數并且存在n^-1^滿足
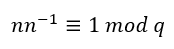
-
FFT
+關注
關注
15文章
434瀏覽量
59403 -
浮點運算
+關注
關注
0文章
19瀏覽量
11180 -
DFT
+關注
關注
2文章
231瀏覽量
22743 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42612 -
NTT
+關注
關注
2文章
51瀏覽量
12963
發布評論請先 登錄
相關推薦




 離散傅里葉變換及其應用簡析
離散傅里葉變換及其應用簡析










評論