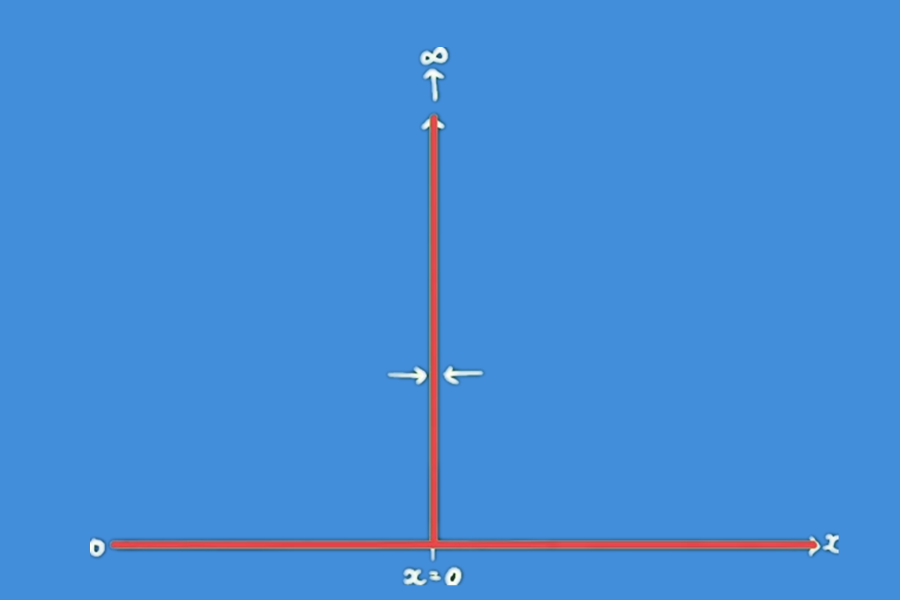
在這篇文章中，我想談一個在物理研究中非常重要的想法，它實際上是一個數學函數，稱為狄拉克δ函數。在x等于0時，δ函數的值非常大，它是無限大。而在x不等于0的其他地方，δ函數的值恒等于0。換句話說，δ函數是一個無限薄且無限大的尖峰。在我們討論δ函數在物理學中的用途之前，我們要先看看δ函數的一些數學特性。

回想一下，對于一般函數，我們是如何求解它的函數圖像與x軸之間的面積的？大多數函數不是由簡單的形狀組成的，但我們可以想象將這個區域分成許多小塊，通過將其視為矩形或梯形來找到每個小塊的面積，然后將它們全部相加得到總的面積，這就是我們對函數進行積分的意思。

考慮到x等于0時，δ函數的寬度為零，它的下方沒有任何面積。但它的高度是無限的，所以我們給了它一個定義，這個函數下的面積最終是有限的，它的面積為1。

δ函數實際上不需要專門在x等于0時處于尖峰，我們實際上可以將尖峰移動到不同的位置。如果我們取因變量x，然后從中減去一些量（假設是 a），則δ(x-a)的函數圖像將移動相同的量a，然后這個函數在x等于a就處于峰值。

這個性質很要的原因是，我們現在可以采用另一個函數，比如說正弦函數sin(x)，然后將它與δ(x-a)想成，最后再對其進行積分，那么我們最終得到的是函數的值sin(a)：。換句話說，當以這種方式使用δ函數時，可以用來挑選任何函數的特定值。

關于δ函數的數學屬性已經足夠了，那么它在物理學中是如何被使用的？盡管這些無窮大并沒有真正出現在現實生活中，但理論物理學中卻充滿了它們的身影。例如，為了簡單起見，我們經常將粒子視為一個點。這意味著，我們假設像電子這樣的小粒子的質量，集中在粒子正中心的一個點上，這個點被稱為質心。

以類似的方式，我們說該電荷集中在一個非常小的點上。事實上，無限小是為了使我們所有的計算變得更容易，而不是必須處理分布在一個小但有限的空間上的電荷。所以在這里，我們就可以使用δ函數對這樣的想法進行數學編碼。

首先，我們考慮的不是粒子的電荷q，而應該是電荷密度ρ。電荷密度是我們在每單位體積中找到的電荷量ρ=q/v，用更正確的方式來說，它實際上是電荷變化dq相對于體積dv的變化率：ρ=dq/dv。現在，我們可以通過這個逆過程，來找到粒子的電荷：q=∫ρdv。

對此的物理解釋是，粒子的電荷可以通過找出空間區域中每個微小體積有多少電荷來給出。我們將電荷密度乘以每個微小體積，得到在此體積中的電荷，然后我們將所有這些電荷相加得到總電荷：q=dq?+dq?+……

但請記住，對于一個簡單的粒子，我們假設電荷實際上根本沒有分布，而是全部在一個點上找到，所以電荷密度用上述所說的定義是不太方便的。事實上，我們可以用δ函數來定義，比如在x=a處：ρ=qδ(x-a)。為什么要這樣做呢，讓我們將其代回積分方程看看會發生什么。

前面我們已經介紹過δ函數的屬性，在這種情況下積分時，δ函數會選出與其相乘的函數的值，所以q=∫ρdv=∫qδ(x-a)dv=q(a)。從數學上講，我們只是用δ函數對q進行編碼。但從物理上來講，δ函數可以幫助我們在帶電粒子實際所在的空間點上找出它。

總結一下，當我們處理帶電粒子時，它們與我們通常習慣的尺度相比是如此之小。當我們必須進行詳細的計算時，我們假設粒子可能無限小并且僅定位于空間中的一個點。在大多數情況下，我們直接使用δ函數是非常合適的，它會使得事情變得更簡單。

δ函數在物理學中還有很多應用，舉一個生活中比較常見的例子。踢足球的時候，我們的腳在會在短時間內對物體進行作用。這時候，我們就可以使用δ函數。只不過，這次不像粒子那樣在空間中定位電荷，而是在時間上定位某個屬性。