我們看到系統的頻率響應可以用極坐標圖表示,其曲線表示頻率從零到無窮大變化的幅度和相位。我們稱之為奈奎斯特圖(或奈奎斯特圖),它是更常見的波德圖的有趣替代品。它提供了我們可以從一階濾波器的奈奎斯特圖中提取的一般信息。
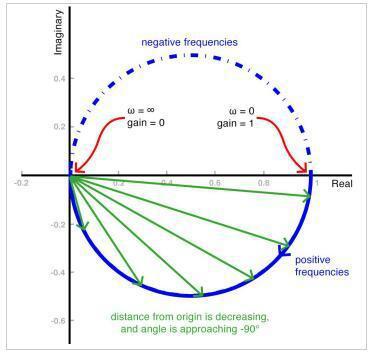
截止頻率的重要性
上圖不包括一條非常重要的信息,即濾波器的截止頻率。一階低通濾波器的s域傳遞函數可表示如下:

這個公式告訴我們,一個給定的低通濾波器的唯一的顯著特點是和ωo。參數K是濾波器的低頻增益。無源元件沒有能力放大的信號,所以,如果我們只關心RC一階低通濾波器,我們可以忽略,因為它永遠是1,其余參數ωo是截止頻率。因此,我們可以簡單地通過指定截止頻率來完整地描述RC低通濾波器。
找到截止頻率
奈奎斯特曲線肯定沒有我們從波德圖中很好地了解到的典型的衰減特性,事實上,奈奎斯特圖并沒有給出關于濾波器電路截止頻率的具體信息。然而,檢查截止頻率和奈奎斯特曲線之間的關系是加強截止頻率概念的一種好方法,它也將使我們對奈奎斯特方法在視覺上描繪頻率響應的局限性有所了解。首先,我們需要考慮關于幅度響應和相位響應的截止頻率實際發生的情況。
通過幅度的截止頻率
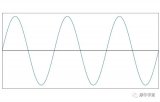
你可能知道截止頻率的另一個名稱是3db(或-3db)頻率,這提醒我們,當輸入頻率為ωo時,一階低通濾波器提供3db的衰減(或相當于-3db的增益)。我們在奈奎斯特圖中不使用分貝,因此代替為-3db,使用相應的振幅比即1/√2。當我們處理極坐標圖時,我們應該始終注意三角形;例如,復數的大小是確定的,就好像它是直角三角形的斜邊,直角三角形的兩條邊是實部和虛部,我們使用三角法來計算復數。既然你在考慮三角形,那么系數1/√2有什么想法嗎?

如上圖所示,當一個直角三角形有兩條等長的邊時,就需要用到因子√2。如果我們把邊的長度減到0.5,斜邊的長度就是√2×0.5,也就是1/√2。

那么,這意味著什么?考慮以下奈奎斯特圖:

這是一階低通濾波器的奈奎斯特圖。請注意,沒有包括與負頻率對應的曲線部分。
如你所見,濾波器在曲線的最低點有1/√2的增益,其中實部分量的絕對值等于虛部分量的絕對值,這是一階低通濾波器奈奎斯特圖中截止頻率的位置。同樣的關系也適用于一階高通濾波器,但在這種情況下,截止頻率在曲線的最高點:

不同之處在于,隨著頻率的增加,高通濾波器的相移從+ 90°變化到0°,而低通濾波器的相位在0°到-90°之間變化。因為角度是從正實軸逆時針測量的,所以在實軸上方繪制正相移,在實軸下方繪制負相移。另請注意,兩個圖的箭頭指向相反的方向:在低通圖中,箭頭指向原點,因為隨著頻率的增加,增益會減小;在高通圖中,它指向遠離原點,因為隨著頻率的增加,增益會增加。
通過相移實現截止頻率
如果我們回想起由一階濾波器產生的90°相移以截止頻率為中心,我們也可以在奈奎斯特圖中找到截止頻率。換句話說,在相移ωo是+ 45°或-45°。在復平面中繪制的矢量在其實部和虛部具有相等的絕對值時將具有+ 45°或-45°的角度,這導致我們從幅度響應的角度考慮截止頻率時發現的相同幾何關系。


奈奎斯特圖中截止頻率的總結
你可能已經注意到,這些奈奎斯特圖中截止頻率的位置是純幾何的。你不能將固定頻率值附加到該位置,因為每個一階低通濾波器或每個一階高通濾波器的位置都相同。奈奎斯特圖顯然不是波特圖的替代品;然而,它是一種更直接的方式來傳達有關系統傳遞函數的信息,正如我們將在之后的文章中看到的那樣,它是穩定性分析中的一個方便工具。
-
低通濾波器
+關注
關注
14文章
496瀏覽量
48318 -
衰減器
+關注
關注
4文章
726瀏覽量
35306 -
高通濾波器
+關注
關注
0文章
100瀏覽量
11525
發布評論請先 登錄
奈奎斯特圖分析怎么判斷穩定性啊?
光電編碼器在最高轉速時,輸出頻率為20KHZ,用DSP進行轉速采集,需要滿足“奈奎斯特”采樣定理嗎?
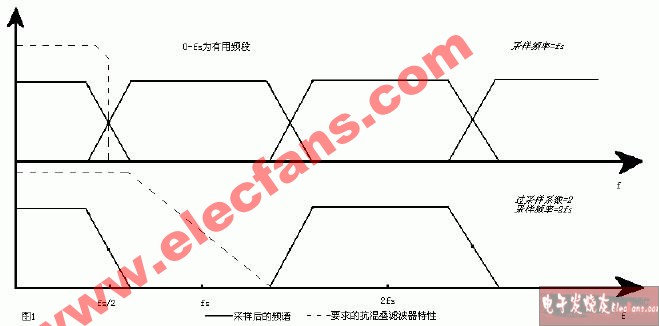
超越第一奈奎斯特區域,將那奎斯特混疊變為優勢
奈奎斯特采樣定理




















評論