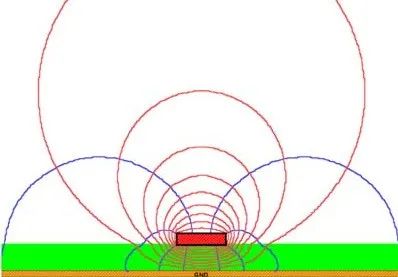
1 基本電磁理論

信號完整性分析是以電磁場理論作為基本理論，所涉及的基本電磁理論基礎包括麥克斯韋方程組、傳輸線理論、匹配理論等。

1. 1 麥克斯韋方程組

經典電磁理論的基石是麥克斯韋方程組，它是描述一切電磁現象的基本規律。

1） 法拉第電磁感應定律：變化的磁場產生電場，對任意的閉合環路：

2） 傳導電流與變化的電場產生磁場：

3） 麥克斯韋方程組

在線性、各向同性媒質中，場量的關系由三個輔助方程：

表示，稱為本構關系。

4） 高頻效應

集膚效應：

在高頻情況下，電磁波進入良導體中會急劇衰減，甚至還不足良導體中一個波長的距離上，電磁波已收到顯著衰減，所以高頻電磁場只能存在良導體表面的一個薄層內，將電磁波場強振幅衰減到表面的1/e的深度稱為趨膚深度：

可以看出，電導率越大，工作頻率越高，趨膚深度越小，導致高頻時的電阻遠大于低頻或直流時的電阻。

鄰近效應：

若干個載流導體間的相互電磁干擾時，各載流導體截面的電流分布與孤立載流導體截面電流分布不同。當相反方向電流的兩導體臨近時，在相互靠近的兩側面最近點電流密度最大；當電流方向相同時，兩外側面的電流密度最小；一般鄰近效應使得等效電阻增大，電感減小。

損耗角：

為了說明媒質在某個頻率上的損耗大小，用損耗角正切來表示，在頻率不高的情況下，損耗角正切代表傳導電流和位移電流密度之比。

1. 2 傳輸線理論

廣義傳輸線是引導電磁波沿一定方向傳輸的導體、介質或由它們組成的導行系統。我們一般所討論的傳輸線是指微波傳輸線，其理論是長線理論，即當傳輸線的幾何尺寸與電磁波的波長可以相比擬時，必須考慮傳輸線的分布參數（或稱寄生參數）。在高速數字或射頻電路設計和高速電路的仿真設計中，許多電磁現象必須應用傳輸線理論進行解釋，傳輸線理論是研究高速數字（或射頻）電路的基礎。

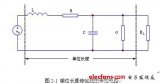
當傳輸信號速率或頻率達到一定時， 傳輸信號通道上的分布參數必須考慮。以平行雙導線為例， 其上的集膚效應帶來單位長度射頻阻抗增大； 到射頻段， 平行雙導線周國的磁場很強， 其寄生電感必須考慮： 平行雙導線間的電場要用電容來等效； 導線間在頻率很高時還要考慮導線間的漏電現象。所以一條單位長度傳輸線的等效電路可由R、L、G 、C 四個元件組成，

傳輸線方程：

方程的通解為：

其中v +, v- 、I+ 、I- 分別是電壓波和電流波的振幅常數，而＋、一分別表示入射波( +Z ）及反射波C - Z ）的傳輸方向。

傳播常數γ定義為：

其中α為衰減常數， β 為相位常數

傳輸線上一點的電壓和電流分別是入射波與反射波的疊加。在Z 軸上任一點的電壓及電流表達式為：

一般傳輸線的特性阻抗定義為傳輸線上行波電壓與行波電流之比，即：對于無

損耗線或低損耗線時：特性阻抗及Z。傳播常數γ分別為：傳輸線上一點的輸

入阻抗定義為傳輸線該點的電壓與電流之比：

1. 3 匹配定理

當負載阻抗與傳輸線特性阻抗不相等， 或連接兩段特性阻抗不同的傳輸線時－ ，由于阻抗不匹配會產生射現象， 從而導致傳輸系統的功率容量和傳輸效率下降，負載不能獲得最大功率。為了消除這種不良反射現象，可在其間接入一阻抗變換器，以獲得良好的匹配。

當RL =Rs 時可得最大輸出功率，稱此狀況為匹配狀態。

當輸入阻抗Zs 與負載阻抗ZL 互為共輒，即Zs =ZL* 時，形成廣義的阻抗匹配。因此，阻抗匹配電路亦可稱為阻抗變換器。