在一個 LTI 系統中,任何時域波形在頻域中有等價的頻譜 。這就意味著任一時域信號完全可以由頻域參數來描述 。
它使電磁模型的頻變性質同時域波形聯系起來,從而我們就可以對總線上以數字比特傳播的信號完整性進行分析 。時域信號以及其等價的頻域描述的關系可由傅里葉變換進行描述:
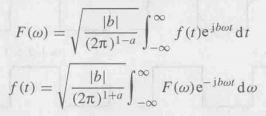
第一個式子將一個時域信號轉換為了頻域形式,而第二個將頻域形式轉換為了時域波形 。 傅里葉變換的慣例是基于 a與 b 的選擇。常用的變換包括現代物理中的( a=0, b=-1 ),系統工程中的( a=1,b=-1),經物理中的(a=1,b=1)以及信號處理中的(a= 0, b=2π)。
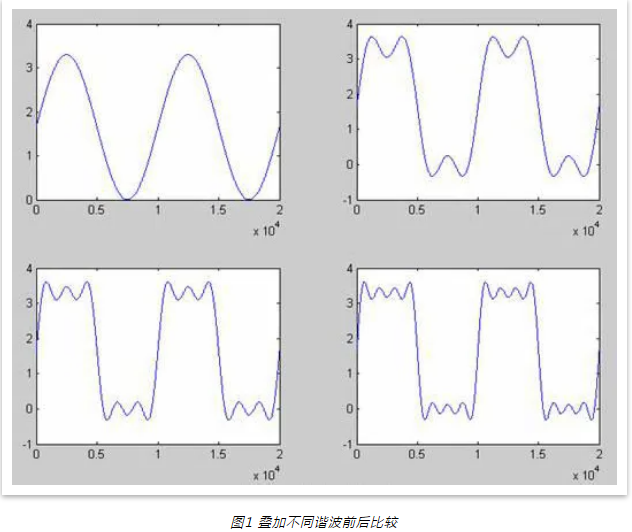
傅里葉變換通過將無限多的正弦函數進行疊加以得到原始的波形,簡單地將時域波形同率響應聯系了起來。例如,如果對一個占空 比為 50% 的方波進行傅里葉展開計算:

對于一個寬為兩個時間單位的理想方波脈沖,如下圖a所示,其頻譜可以利用系統工程變換(a=1,b=-1) 來計算得到:



上式為方波脈沖的頻譜,如下圖b,可以看到方波頻域為一個sinc函數。

一個方波脈沖可作為一個數字比特的一階逼近,但其更好的逼近為梯形波 。 如下圖展示了一個梯形披同理想方波的頻率響應的對比。
注意到梯形波頻率響應的形狀同方波是非常相似的,僅僅是諧波的幅度要小一些,在高頻下這種現象更明顯 。
這就說明了另一個重要概念:數字波形的上升與下降時間決定了其在頻域范圍內的高頻諾波的幅度 。

上圖同樣說明了我們也可以通過在方波的頻譜上外加一個低通濾波函數來得到一個梯形波的頻譜。這樣就可以定義出一個數字波形的譜分量同其上升與下降時間之間的關系 。
要得到這一關系,首先要來觀察方波頻譜自身的一些特點 。方波頻譜函數表明方波的諧波為 sine 函數。對 sine 函數取極限就得到歸一化的頻譜:

一種得到近似梯形披頻譜的方法是對方波的諧波外加一個低通濾披函數,直到能得到梯形波所描述的上升與下降時間 。
外加濾波器的最簡單的方法是應用一個單極點低通濾披響應,比如 RC 網絡。一個簡單的單極點濾波器的階躍響應為:

其中,Vinput為濾波器的輸入電壓,Vout為輸出電壓,τ為時間常數 。如果將上升時間用電壓幅值的 10% 與 90% 來定義,那么就可以計算出具體的t10%~t90%下降一階時所需的時間常數。當單位階躍通過一個時間常數為τ的單極點濾波器時,其上升時間為

注意 t10%與t90%是分別由 0. 1=1-exp(-t10%/τ)和0. 9=1-exp(-t90%/τ)計算得出的 。單極點濾波器的 3 dB 帶寬為:

則邊沿譜分量與上升時間的關系式:

上式是數字信號頻譜帶寬的上升下降時間的較好粗略計算。
另外,更為普通的關系表達為:

對于高斯脈沖 K=0.338 對于單極指數衰減脈沖 K=0.350 對于大多數的數字信號 這0種小變化是沒有什么關系的。
-
低通濾波器
+關注
關注
14文章
478瀏覽量
47483 -
衰減器
+關注
關注
4文章
640瀏覽量
34405 -
信號完整性
+關注
關注
68文章
1413瀏覽量
95559 -
信號處理器
+關注
關注
1文章
254瀏覽量
25314 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42662
發布評論請先 登錄
相關推薦
示波器的那些事-示波器上升時間
【連載筆記】信號完整性-EMI與頻域、正弦波、帶寬與上升時間
數字電路測量示波器探頭的上升時間和帶寬
關于信號上升時間和傳輸延時的關系
BOB示波器信號上升時間的劣化
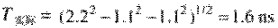
BOB示波器輸入信號上升時間的測量
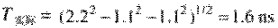




 數字信號頻譜帶寬的上升時間F_3dB=0.35/Tr是怎么來的?
數字信號頻譜帶寬的上升時間F_3dB=0.35/Tr是怎么來的?

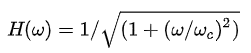










評論