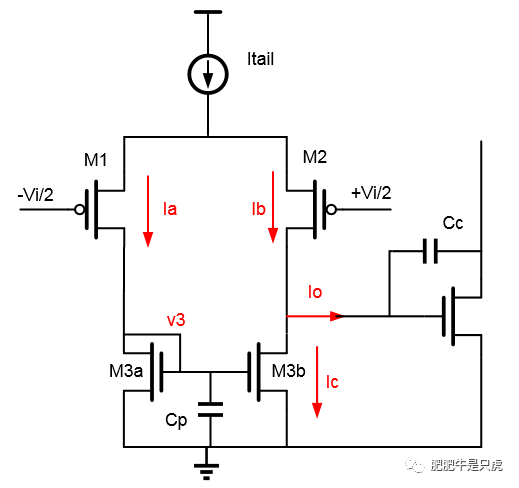
單端輸出的5管運放或者電流鏡存在一對高頻零極點對，本文試圖從多個角度推導、理解這個零點。

• 小信號圖方法

先考慮低頻情況，即不考慮寄生電容Cp

Ia = Ic = gm1*Vi/2

Ib = -gm1*Vi/2

輸出電流Io = Ib-Ic = -gm1*Vi

再考慮一般情況，即考慮寄生電容Cp的影響

v3所在點的等效阻抗為 1/gm3和Cp的并聯，Zeq=1/gm3*1/(1+sCp/gm3)

Ia = gm1*Vi/2

V3 = Ia Zeq = Vi/2 (gm1/gm3)*1/(1+sCp/gm3)

M3b的電流 Ic = V3gm3=Vi/2gm1/(1+sCp/gm3)

Ib = -gm1*Vi/2

輸出電流 Io = Ib-Ic = -Vi/2 gm1 [1 + 1/(1+sCp/gm3)]

上式通分得到 Io = -Vi/2gm1 num/den

其中num = 2 + s*Cp/gm3

den = 1+ s*Cp/gm3

令num = 0，得到零點 z=-2*gm3/Cp

令den = 0，得到極點 p=-gm3/Cp

結論：

鏡像電流鏡處存在一對左半平面的零極點對，零點為極點的2倍

z = - 2*gm3/Cp

p=-gm3/Cp

1. 零極點的物理意義

極點：

由電阻1/gm3和Cp組成的RC并聯網絡在電流的驅動下形成極點頻率。

零點：

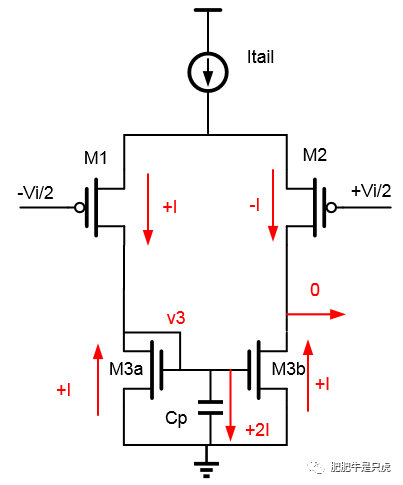
當頻率足夠高時，Cp的阻抗足夠低，流過Cp的電流足夠大，改變通過M3a和M3b的電流的極性。

在零點頻率處，流過各個器件的電流及其方向見下圖。

1. 更抽象的理解方式

大家應該聽過類似的表達，“信號通過兩條不同的路徑到達同一個目的地，會形成零點。”我們試圖將這個說法抽象化、模型化，并證明其合理性。

假設信號通過兩條不同的路徑（分別為路徑A、路徑B）到達目的地，兩條路徑的傳函分別為：

A通路：A1(s) = A1/(1-s/p1)

B通路：A2(s) = A2/(1-s/p2)

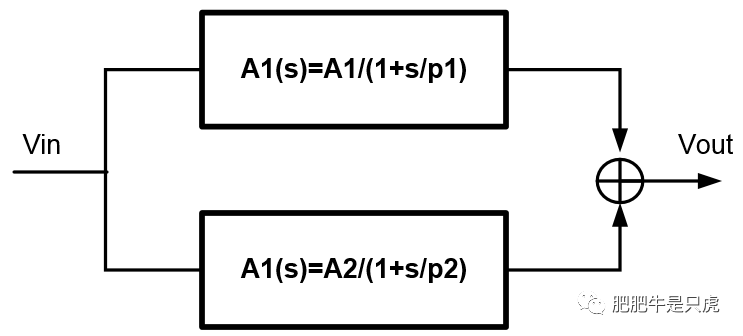
Vout/Vin = A1/(1-s/p1) + A2/(1-s/p2)

對上式進行通分化簡

Vout/Vin = （A1+A2）*num/den

其中num = 1 - s/(A1+A2)*(A1/p2+A2/p2)

den  = (1-s/p1)(1-s/p2)

令num=0，得到零點 z = (A1+A2)/(A1/p2+A2/p1)

令den=0，得到極點 p1、p2

具體到鏡像電流鏡應用 ，也是兩條通路，

快通路：從M2直接到輸出，傳函 I1(s) = I/(1-s/p1)，其中p1為輸出極點

慢通路：從M1-->M3a-->M3b-->輸出，

慢通路傳函：I2(s) = -I/(1-s/p1)/(1-s/p2)，其中p2為鏡像極點

總的傳函：Io(s) = I1(s) - I2(s) = I*(2-s/p2)/[(1-s/p1)(1-s/p2)]

很顯然，零點 z=2*p2
至此，我們通過這種抽象建模，也證明了鏡像零點的存在，且推導了其精確表達式。