虛零點(diǎn)法
虛零點(diǎn)法是指引入的對(duì)應(yīng)零點(diǎn)只出現(xiàn)在環(huán)路增益A(s)F(s)中,而不出現(xiàn)在閉環(huán)傳遞函數(shù)H(S)中,能夠?qū)崿F(xiàn)此目的的零點(diǎn),只能是在反饋環(huán)路F(S)中引入的零點(diǎn),現(xiàn)假設(shè)反饋環(huán)路F(s)=F1(s)(n1+s),F(S)中存在一個(gè)零點(diǎn)n1,則:

在反饋通道中引入的零點(diǎn)就是虛零點(diǎn),原則上可以在反饋網(wǎng)絡(luò)的以下三個(gè)位置引入虛零點(diǎn):
- 反饋網(wǎng)絡(luò)中間
- 反饋網(wǎng)絡(luò)的輸入端,即放大器的輸出端
- 反饋網(wǎng)絡(luò)的輸出端,即放大器的輸入端
- 虛零點(diǎn)對(duì)根軌跡的影響
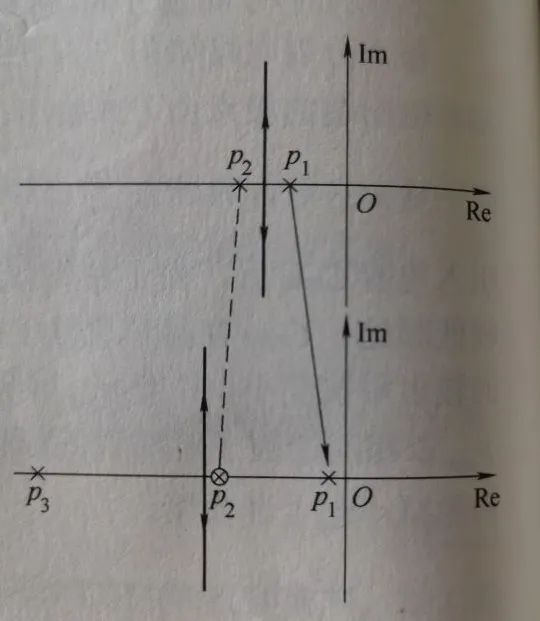
虛零點(diǎn)應(yīng)該如何放置才可以獲得期望的頻率補(bǔ)償?下面以常見的二階系統(tǒng)為例,假設(shè)其環(huán)路增益有兩個(gè)極點(diǎn)p1、p2和一個(gè)零點(diǎn)n1,則其根軌跡特征方程式可以表示為:

我們費(fèi)了半天勁推導(dǎo)以上公式,目的是什么?可能很多讀者有點(diǎn)迷惑,在此鄭重聲明如下:費(fèi)了半天勁推導(dǎo)以上公式,不是為了保衛(wèi)宇宙和平,我們推導(dǎo)的目的,就是要根據(jù)要求的頻率補(bǔ)償而計(jì)算所需要的補(bǔ)償零點(diǎn)位置!
比如,現(xiàn)在我們想把一個(gè)低通特性的系統(tǒng)的頻率特性補(bǔ)償為巴特沃斯特性,我們知道巴特沃斯低通的原型分母可以寫為:

2.虛零點(diǎn)在放大器的輸入端實(shí)現(xiàn)
虛零點(diǎn)在輸入端實(shí)現(xiàn)時(shí),使用什么類型器件主要取決于源阻抗的類型(是電阻、還是電容、電感)以及使用何種反饋網(wǎng)絡(luò),如下圖:
下面兩圖的Zp為虛零點(diǎn)補(bǔ)償元件,Zs為源阻抗,兩圖分別在放大器輸入端補(bǔ)償,而等效在反饋網(wǎng)絡(luò)的輸出端引入虛零點(diǎn):
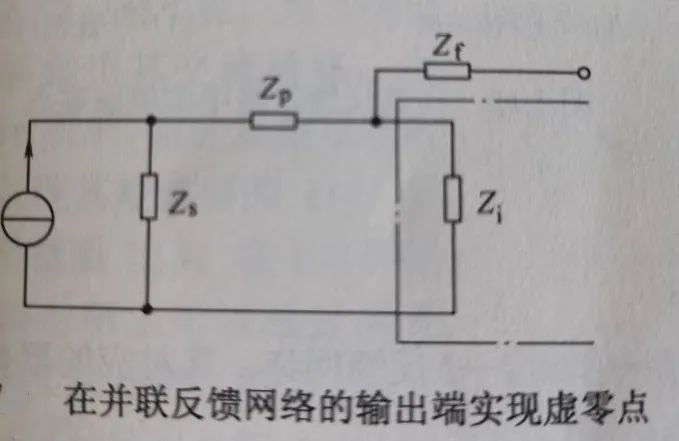
對(duì)于輸入并聯(lián)負(fù)反饋,補(bǔ)償元件Zp的選擇如下:
1)若Zs為電阻,則Zp為電感
則補(bǔ)償后的阻抗由Zs=Rs,變?yōu)镽s+s*L,引入一個(gè)左半平面的零點(diǎn);而且低頻時(shí)Zp可以忽略,傳遞特性保持補(bǔ)償前的狀態(tài),這正是前述公式推導(dǎo)的基本假設(shè)要求,也是我們?cè)诘谝黄l率補(bǔ)償推文中提到的:頻率補(bǔ)償不是完全推翻原特性,而是局部修改頻率特性,它不應(yīng)該改變整體趨勢(shì);如要改變整體頻率特性,那就不叫頻率補(bǔ)償了,那是重新設(shè)計(jì)。
復(fù)雜的模擬電路設(shè)計(jì),涉及方方面面的指標(biāo),各種指標(biāo)間相互牽扯,就是著名的八邊形法則,見模擬集成電路大神”拉扎微”的書的第43頁(yè),如下:

各種指標(biāo)設(shè)計(jì)相互掣肘,我們?cè)撊绾蜗率郑恳话憧梢园凑赵肼?>失真=>頻率補(bǔ)償...等順序來(lái)做,具體緣由以后推文再說,可見頻率補(bǔ)償并不是推翻了重新設(shè)計(jì),而是在噪聲、失真原設(shè)計(jì)結(jié)構(gòu)的基礎(chǔ)上,微調(diào)頻率特性,調(diào)整太大,前期噪聲、失真階段的設(shè)計(jì)成果就完全作廢了。
2)若Zs為電容,則Zp為電阻和(或)電感
則補(bǔ)償后的阻抗由Zs=1/sc,變?yōu)?/sc+sL或1/sc+R或1/sc+sL+R,引入一個(gè)左半平面的零點(diǎn)
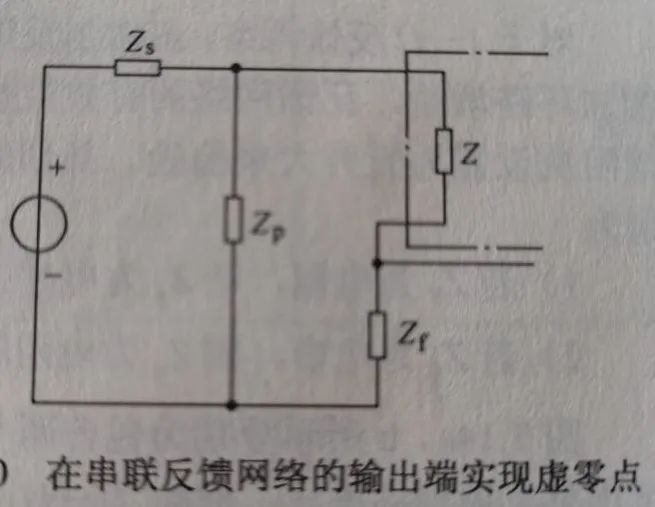
1)若Zs為電阻,則Zp為電容
2)若Zs為電感,則Zp為電阻和(或)電容
在放大器輸入端實(shí)現(xiàn)虛零點(diǎn),應(yīng)該注意補(bǔ)償器件對(duì)噪聲的影響,由于補(bǔ)償電阻的噪聲直接加在放大器輸入端,可能破壞前期的噪聲設(shè)計(jì)指標(biāo)。所以前期噪聲設(shè)計(jì)應(yīng)該留有余量。
3.虛零點(diǎn)在放大器的輸出端實(shí)現(xiàn)
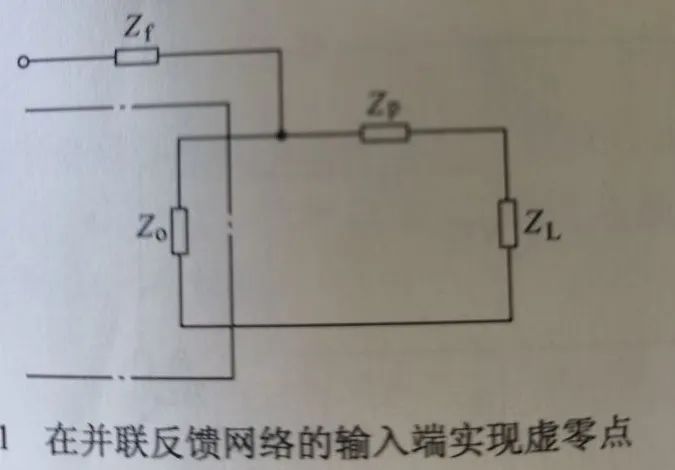
上圖為輸出電壓負(fù)反饋,Zp為零點(diǎn)補(bǔ)償元件:
1)若負(fù)載ZL為電阻,則Zp可為電感
2)若負(fù)載ZL為電容,則Zp為電阻和(或)電感
下圖為輸出電流負(fù)反饋:
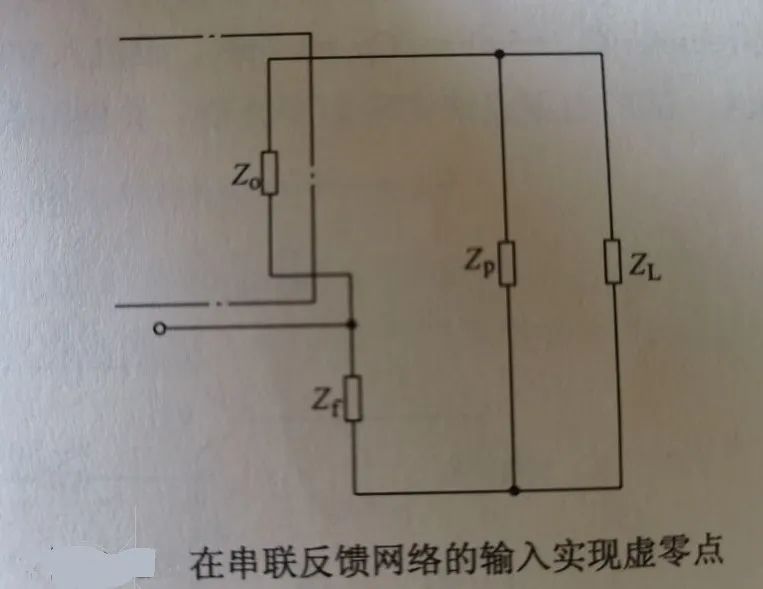
上圖為輸出電流負(fù)反饋,Zp為零點(diǎn)補(bǔ)償元件:
1)若負(fù)載ZL為電阻,則Zp可為電容
2)若負(fù)載ZL為電感,則Zp為電阻和(或)電容
4.虛零點(diǎn)在放大器的反饋網(wǎng)絡(luò)中的實(shí)現(xiàn)
與放大器輸入或輸出實(shí)現(xiàn)虛零點(diǎn)不同,在反饋網(wǎng)絡(luò)中的虛零點(diǎn)不僅影響系統(tǒng)噪聲,還會(huì)影響系統(tǒng)的失真特性,如下:

對(duì)于U-I型補(bǔ)償結(jié)構(gòu):
- 若Zf為電阻,則補(bǔ)償元件Zp為電容
- 若Zf為電感,則補(bǔ)償元件Zp為電阻和(或)電容
對(duì)于I-U型補(bǔ)償結(jié)構(gòu):
- 若Zf為電阻,則補(bǔ)償元件Zp為電感
- 若Zf為電容,則補(bǔ)償元件Zp為電阻和(或)電感
補(bǔ)償也可采用U-U結(jié)構(gòu)或I-I結(jié)構(gòu),而U-U結(jié)構(gòu)可以開成由U-I、I-U構(gòu)成的雙反饋網(wǎng)絡(luò),反饋元件類型選擇同單反饋結(jié)構(gòu):

5.設(shè)計(jì)應(yīng)用舉例

上圖是晶體管構(gòu)成的兩級(jí)電壓串聯(lián)負(fù)反饋電路,其放大倍數(shù)通過估算,一看就知道基本上為10倍,假設(shè)晶體管的

如前所述,下圖把可能的頻率補(bǔ)償位置與補(bǔ)償元件都列舉出來(lái),實(shí)際補(bǔ)償往往只選一個(gè)位置:
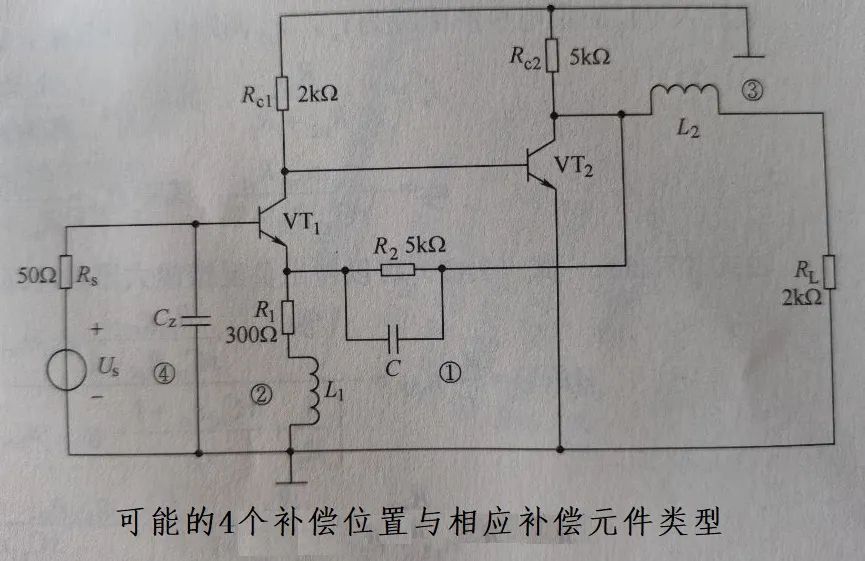
上圖①、②為反饋網(wǎng)絡(luò)中的雙補(bǔ)償,
③為反饋網(wǎng)絡(luò)輸入端的虛零點(diǎn)補(bǔ)償,
4為反饋網(wǎng)絡(luò)輸入端的虛零點(diǎn)補(bǔ)償。具體看查看前述推文。
選定①補(bǔ)償方式,則其環(huán)路增益計(jì)算如下:

注意斷點(diǎn)的位置,環(huán)路增益計(jì)算是從斷點(diǎn)位置右側(cè)沿環(huán)路一周,計(jì)算到斷點(diǎn)左側(cè),斷點(diǎn)可以是環(huán)路中的任意位置,原則就是要方便計(jì)算:
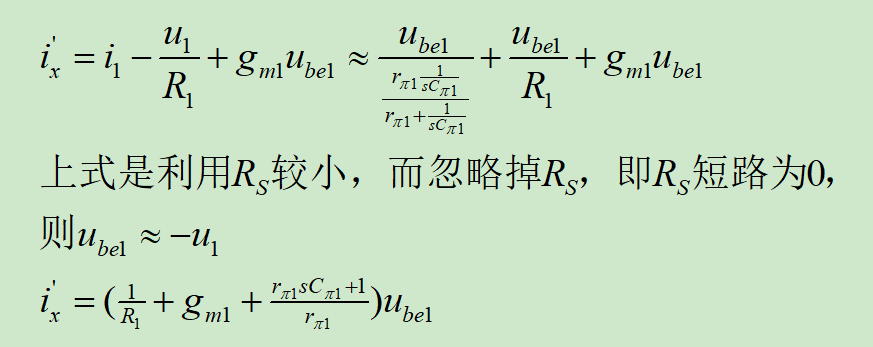
由于R2>>R1,則

-
放大器
+關(guān)注
關(guān)注
143文章
13627瀏覽量
214000 -
電阻器
+關(guān)注
關(guān)注
21文章
3796瀏覽量
62256 -
CMOS集成電路
+關(guān)注
關(guān)注
4文章
41瀏覽量
14273 -
二階系統(tǒng)
+關(guān)注
關(guān)注
1文章
16瀏覽量
9601 -
負(fù)載電容
+關(guān)注
關(guān)注
0文章
141瀏覽量
10463
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
分享一份CMOS模擬集成電路設(shè)計(jì)手冊(cè)
cmos射頻集成電路設(shè)計(jì)

CMOS模擬集成電路設(shè)計(jì).2版-艾倫
模擬CMOS集成電路設(shè)計(jì):零極點(diǎn)對(duì)消




 模擬CMOS集成電路設(shè)計(jì):虛零點(diǎn)法
模擬CMOS集成電路設(shè)計(jì):虛零點(diǎn)法










評(píng)論