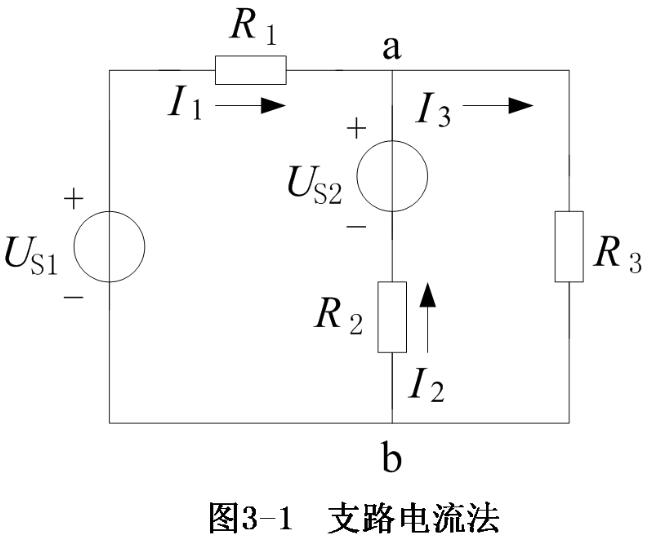
在電路中，任何支路上流過的電流都只能是單值的。針對圖1中a點的情況可以發現，流出該點的電流比流入的電流大，實際上這是不可能的。因此，不同量值的電流源是不能串聯連接的，就像不同量值的電壓源不能并聯一樣。

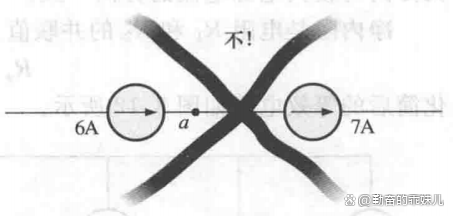
圖1

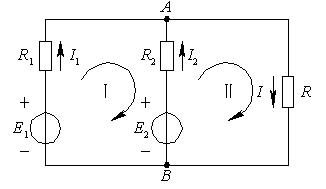
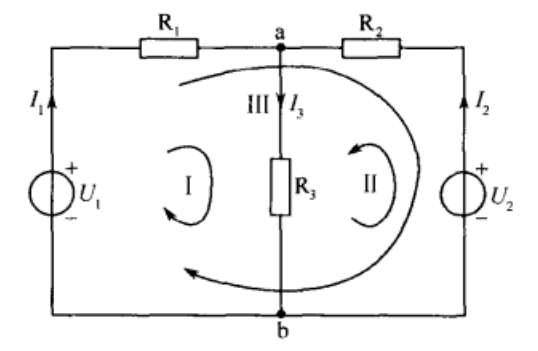
在詳細討論第一個重要的分析方法之前，讓我們一起來分析圖2中的電路，從而更好地理解為什么需要這些特殊的方法來分析電路。

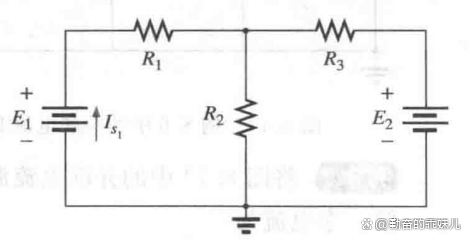
圖2

初看上去，我們可以使用化簡和反推法向電源E1方向化簡，并計算出電源電流Is~~1 。然而串聯元件R3和E2是不同類型的元件，所以不能合并。進一步觀察可以發現，這個電路沒有兩個同類元件是串聯或并聯的。因此不能對元件進行合并，這就明顯指出，必須使用另外的方法來求解這個電路。

必須指出，如果我們將每個電壓源轉換為電流源，然后合并它們，那么就可以求解出圖2所示的電路。然而，如果要求解原電路中的某個具體的值，那么就需要利用從電源變換中求得的量往回計算出待求的量。

本次介紹的方法稱為支路電流法或支路分析法，這是因為我們將要定義和求解電路中每條支路的電流。介紹這個方法并讓大家理解它的應用的最好辦法就是總結出一系列的步驟，每個步驟都是精心給出的。下面例子的求解就遵循了這些步驟。

支路電流法分析步驟

1)給電路中的每條支路都標上一個電流，電流的方向任意。

2)根據假定的電流方向，標出每個電阻電壓的極性。

3)對電路中每個獨立的閉合回路應用基爾霍夫電壓定律。

確定需要應用多少次基爾霍夫電壓定律的最好方法就是先確定電路中“窗口”(或網孔)的數量。例1中的電路和圖2a的結構非常相似，都是兩窗口。結果就需要應用基爾霍夫電壓定律兩次。對于有三個窗的電路，如圖2b，則需要應用基爾霍夫電壓定律三次，依此類推。

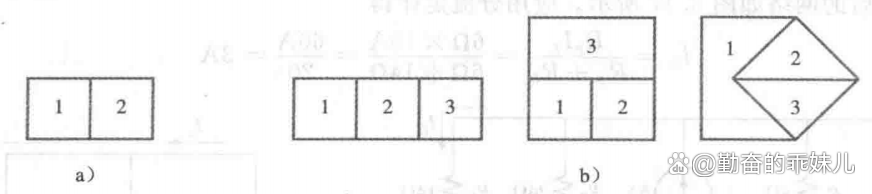
圖2

4)在最少個數的節點處應用基爾霍夫電流定律，并且包含網絡的所有支路電流。

最少個數就是電路中總節點的個數減1。為了進行說明，規定一個節點就是兩個或多個支路的交叉點，其中的支路可以是任意串聯元件的組合。圖3中給出了圖2的每個結構需要應用基爾霍夫電流定律的次數。

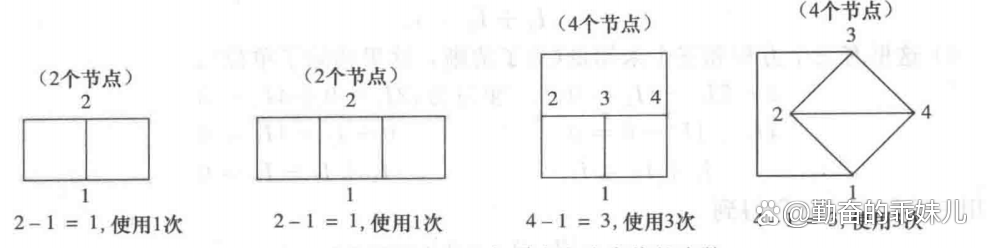
圖3

5)根據得到的聯立線性方程組，求解假定的支路電流。

假定求解電流I1、I2和I3時使用的行列式方法大家都能理解，并且在數學課中已經學習了這部分內容。使用計算器和計算機軟件包，例如MATLAB和Mathcad，可以快速準確地計算出結果。

例1.利用支路電流法求解圖4中的電路。

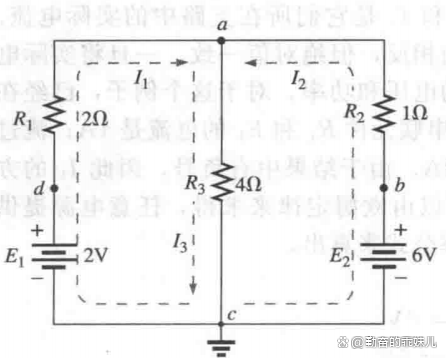
圖4

解.

1)由于有三個不同的支路(cda，cba，ca),因此選擇了三個任意方向的電流(I 1 、I 2 ，I 3 )，如圖4所示。選擇電流I1和I2的方向，使其分別與電源E1和E2的電動勢方向相同。由于I1和I2都流入節點a，因此將I3標注為流出節點。

2)畫出每個電阻上電壓的極性，使其與假定的電流方向一致，如圖5所示。

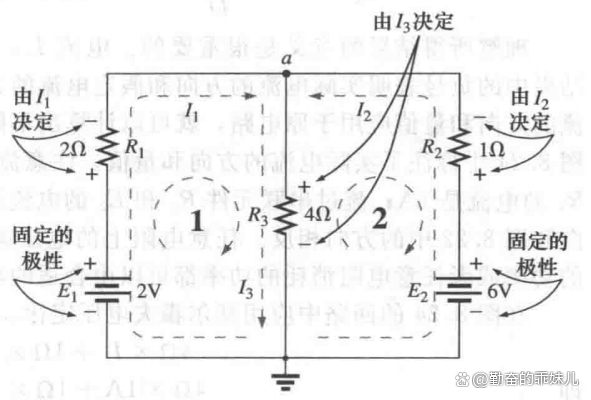
圖5

4)在節點a應用基爾霍夫電流定律(在兩節點電路中，只需在其中一個節點處應用這個定律)得

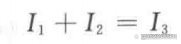
5)這里有三個方程和三個未知量(為了清晰，這里移除了單位):

使用三階行列式我們得到

負號只是表示實際電流的方向和假定電流的方向相反。

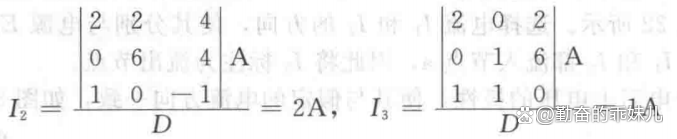
理解所得結果的意義是很重要的。電流I 1， I2和I3 是它們所在支路中的實際電流。結果中的負號表明實際電流的方向和假定電流的方向相反，但絕對值一致。一旦將實際電流的方向和量值應用于原電路，就可以計算出不同的電壓和功率。

對于這個例子，已經在圖6中標注了實際電流的方向和量值。注意流過串聯元件R1和E1的電流是1A；流過R3的電流是1A；流過串聯元件R2和E2的電流是2A。由于結果中有負號，因此I1的方向和圖4中的方向相反。任意電阻上的電壓都可以由歐姆定律來求得，任意電源提供的功率或者任意電阻消耗的功率都可以由合適的功率公式來算出。

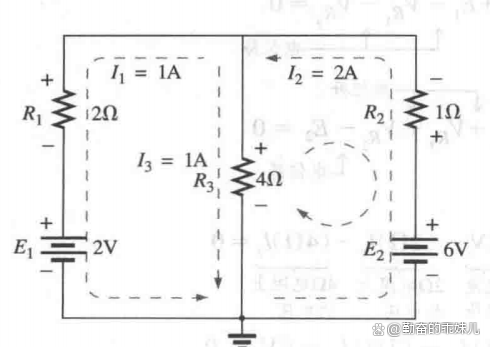
圖6

在圖6的回路中應用基爾霍夫電壓定律，得

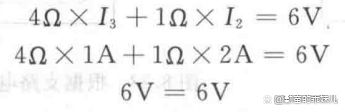
這就驗證了結果的正確性。