本文在二維極坐標(biāo)下建立了在定子齒上開輔助槽的表貼式永磁電機(jī)空載時的磁場解析模型。如圖1所示,電機(jī)被分為5個求解子域:子域Ⅰ(永磁體),子域Ⅱ(氣隙),子域Ⅲ(電樞槽),子域Ⅳ(電樞槽開口),子域Ⅴ(輔助槽)。以矢量磁位為位函數(shù),在各個子域建立拉普拉斯方程或泊松方程,推導(dǎo)了電機(jī)空載時相關(guān)性能參數(shù)的計(jì)算公式。然后,以一臺32極48槽的電動車用表貼式外轉(zhuǎn)子輪轂永磁電機(jī)為例,通過有限元法和齒槽轉(zhuǎn)矩實(shí)驗(yàn)對該解析模型的有效性和精確性進(jìn)行了驗(yàn)證,并基于該解析模型對影響該輪轂電機(jī)齒槽轉(zhuǎn)矩的相關(guān)參數(shù)進(jìn)行了優(yōu)化,削弱了齒槽轉(zhuǎn)矩。
1 解析模型
1.1 基本假設(shè)
本文以外轉(zhuǎn)子表貼式永磁電機(jī)進(jìn)行模型推導(dǎo)和計(jì)算,該模型也同樣適用于內(nèi)轉(zhuǎn)子永磁電機(jī)。圖1所示為表貼式永磁電機(jī)的1/4截面示意圖。為了便于分析,需做以下假設(shè):
(1)定、轉(zhuǎn)子鐵芯材料的磁導(dǎo)率無窮大;
(2)在二維平面內(nèi),忽略電機(jī)的端部效應(yīng);
(3)永磁體的退磁特性為線性;
(4)定子槽、槽開口、輔助槽均為形狀規(guī)則的徑向扇形結(jié)構(gòu),如圖1所示;
(5)假定永磁體之間間隙的相對磁導(dǎo)率與永磁體的相同,永磁體的相對磁導(dǎo)率μr≠1。
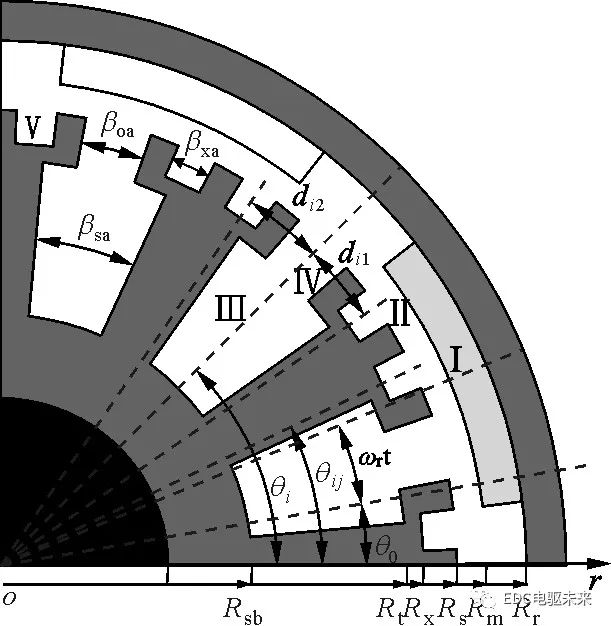
圖1 永磁電機(jī)各子域的符號和定義
在圖1中:將二維極坐標(biāo)系(r,θ)固定在定子上,且規(guī)定齒的中心線位置為θ=0°;θ0為轉(zhuǎn)子在最初位置時磁極的N極中心線與定子(θ=0°)的夾角;ωr為轉(zhuǎn)子的旋轉(zhuǎn)角速度;βsa為電樞槽寬角;βoa為電樞槽開口寬角;βxa為輔助槽寬角;dij為第i個槽兩側(cè)的第j個輔助槽中心線距槽中心位置的寬度角;θi為第i個槽和槽開口的中心位置:θi=2π/Ns(i-1/2),其中Ns為電機(jī)槽數(shù);θij為第i個電樞槽對應(yīng)的第j個輔助槽的中心位置,θij=θi+dij。
1.2 各子域的矢量磁位方程
磁場與矢量磁位的關(guān)系為
 2A=-
2A=- ×B
×B
(1)
在二維平行平面場中,矢量磁位A僅有z方向分量,故有
Azy=Azyez
(2)
可得各子域的矢量磁位方程為
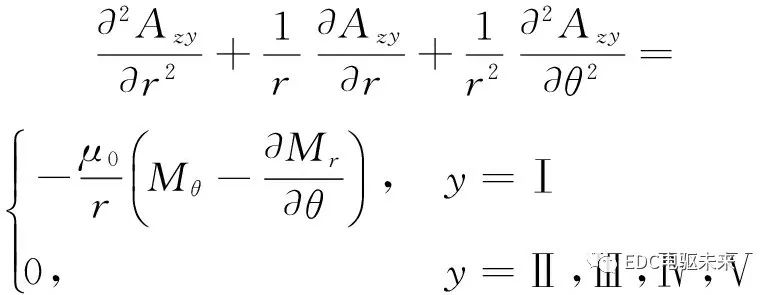
(3)
式中:Azy為矢量磁位,下角標(biāo)y代表不同子域。
1.3 永磁體子域
在永磁體區(qū)域中,剩余磁化強(qiáng)度M可表示為
M=Mrr+Mθθ
(4)
式中:Mr和Mθ是永磁體剩余磁化強(qiáng)度的徑向和切向分量[15]。
由于轉(zhuǎn)子鐵芯的磁導(dǎo)率為無窮大,故沿著轉(zhuǎn)子軛(r=Rr)邊界滿足條件
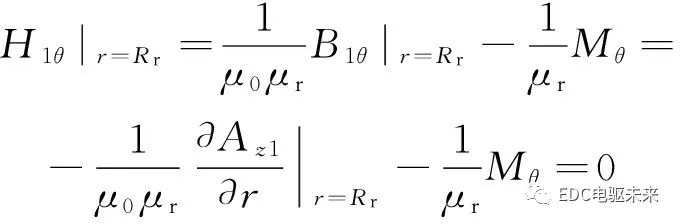
(5)
通過分離變量法,利用以上邊界條件求得永磁體子域的矢量磁位表達(dá)式為
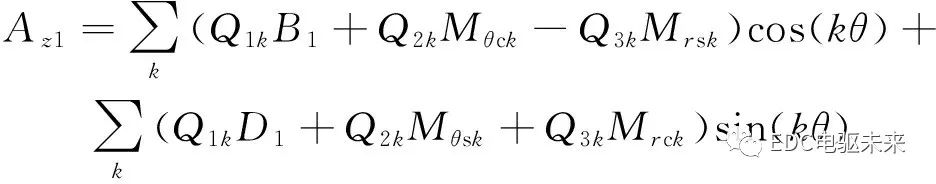
(6)
式中
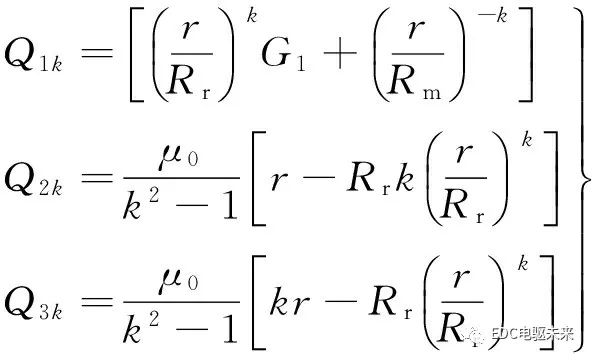
(7)
Mθck、Mθsk、Mrck、Mrsk可參見文獻(xiàn)[15];B1、D1是需要求解的諧波系數(shù);k為諧波階次。
1.4 氣隙子域
通過分離變量法,求得氣隙子域的矢量磁位
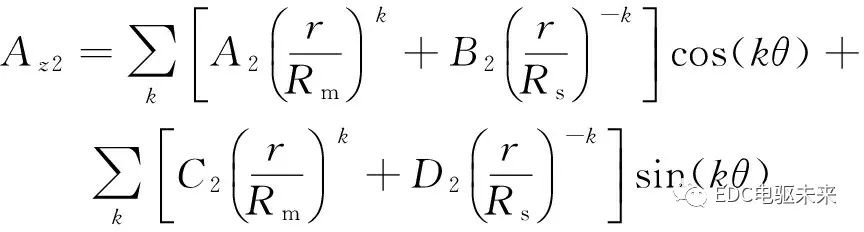
(8)
式中:A2、B2、C2、D2為待求解的氣隙子域的諧波系數(shù)。
1.5 電樞槽子域
由于鐵芯磁導(dǎo)率為無窮大,所以電樞槽子域的2個邊界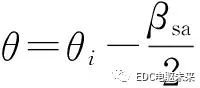 和
和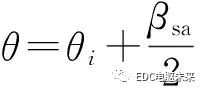 處的邊界條件為
處的邊界條件為
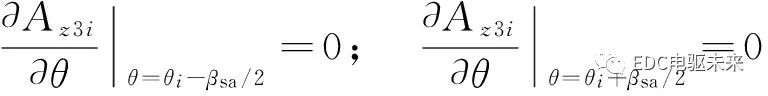
(9)
沿著電樞槽底部的邊界滿足
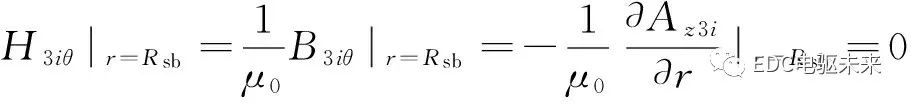
(10)
根據(jù)分離變量法以及式(9)和式(10)的邊界條件,可求得第i個槽子域的矢量磁位表達(dá)式為
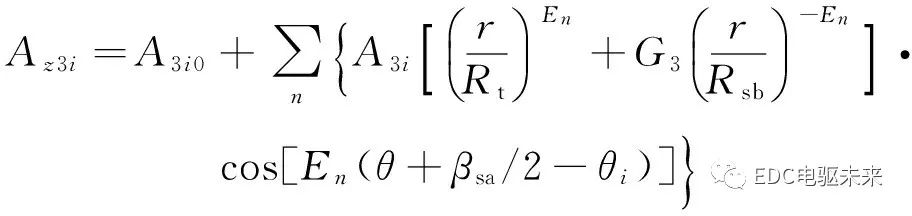
(11)
式中
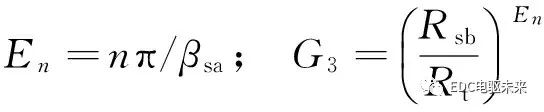
(12)
A3i0、A3i是待求解的諧波系數(shù);n為諧波階次。
1.6 槽開口子域
槽開口子域2個邊界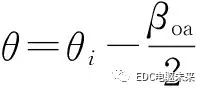 和
和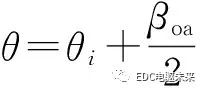 處的邊界條件為
處的邊界條件為
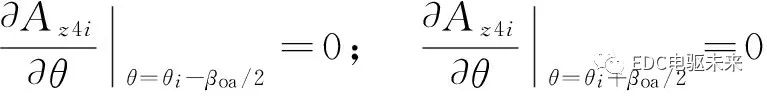
(13)
通過分離變量法解得第i個槽開口子域的矢量磁位通解為
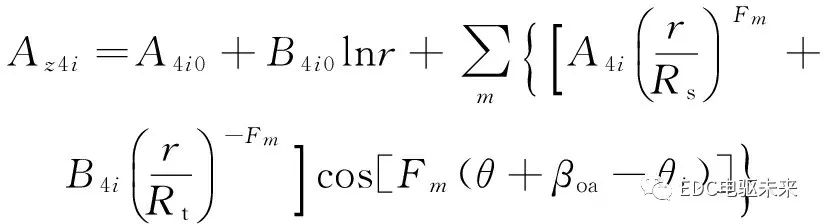
(14)
式中
Fm=mπ/βoa
(15)
A4i0、B4i0、A4i和B4i是待求解的諧波系數(shù);m為諧波階次。
1.7 輔助槽子域
輔助槽子域的2個邊界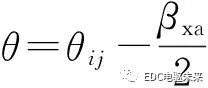 和
和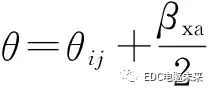 處的邊界條件為
處的邊界條件為
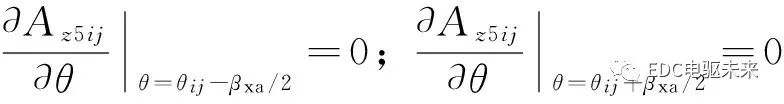
(16)
沿著槽底部的邊界滿足
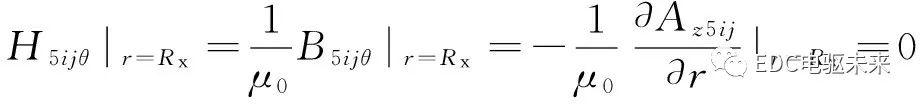
(17)
根據(jù)分離變量法以及式(16)和式(17)的邊界條件,可求得第(i-1)Nx+j個輔助槽子域的矢量磁位通解為
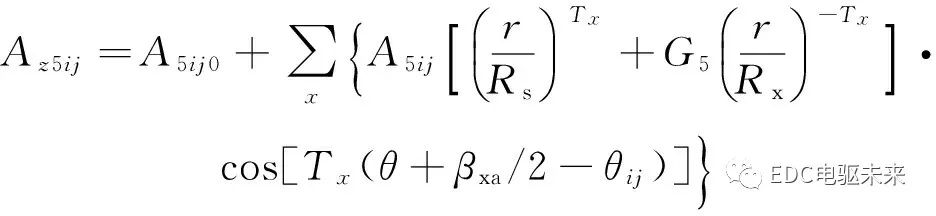
(18)
式中
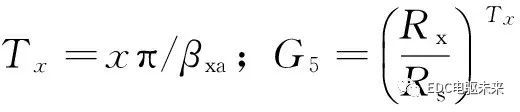
(19)
A5ij0、A5ij是待求諧波系數(shù);Nx為每齒上的輔助槽數(shù);x為諧波階次。
2 根據(jù)分界面條件求解諧波系數(shù)
根據(jù)徑向磁通密度連續(xù)性和切向磁場強(qiáng)度連續(xù)性,可得各子域之間的分界面條件,進(jìn)而求解諧波系數(shù)。矢量磁位與磁通密度的關(guān)系為
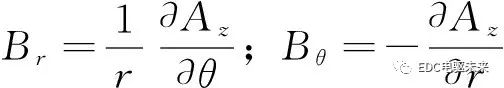
(20)
2.1 永磁體子域和氣隙子域的分界面(r=Rm)
永磁體子域和氣隙子域分界面(r=Rm)的條件為
Az1|r=Rm=Az2|r=Rm
(21)
H1θ|r=Rm=H2θ|r=Rm
(22)
根據(jù)子域1、2中磁通密度B與磁場強(qiáng)度H的關(guān)系,式(22)可變換為
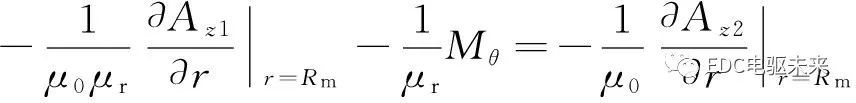
(23)
2.2 電樞槽開口子域和氣隙子域的分界面(r=Rs)
由于定子鐵芯的磁導(dǎo)率為無窮大,所以沿著電樞槽開口子域和氣隙子域的分界面(r=Rs),在[0,2π]整個圓周的切向磁通密度分布函數(shù)為

(24)
故該分界面的條件為
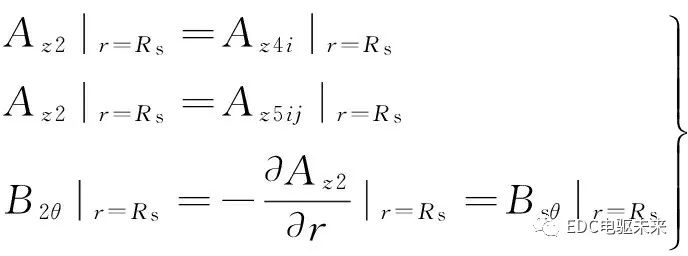
(25)
2.3 電樞槽子域和電樞槽開口子域分界面(r=Rt)
沿著電樞槽子域和電樞槽開口子域分界面(r=Rt),在電樞槽子域范圍(θi-βsa/2≤θ≤θi+βsa/2)的切向磁通密度分布函數(shù)為
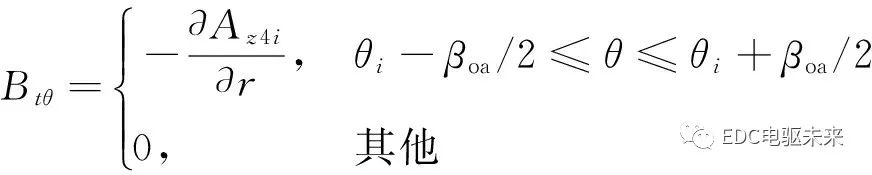
(26)
故該分界面的條件為
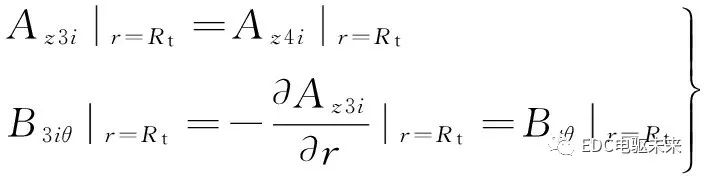
(27)
將以上得到的各子域之間的分界面條件作傅里葉級數(shù)展開(見附錄A),并聯(lián)立方程組,可求得前述各個子域的諧波系數(shù)。
3 磁場解析計(jì)算與驗(yàn)證
以一臺32極48槽的電動車用外轉(zhuǎn)子表貼式永磁輪轂電機(jī)為研究對象,其參數(shù)如下:極數(shù)2p=32,槽數(shù)Ns=48,槽寬角βsa=3.79°,充磁方式為徑向,齒尖邊緣高(Rs-Rt)=2 mm,軸向長度la=40 mm,槽底半徑Rsb=104.5 mm,額定轉(zhuǎn)速為600 r/min,槽開口底部半徑Rt=140.3 mm,永磁體厚度為6.3 mm,槽開口頂部半徑Rs=142.3 mm,磁通密度Br=1.2 T,永磁體表面半徑Rm=143.5 mm,永磁體磁導(dǎo)率μr=1.05,轉(zhuǎn)子軛內(nèi)表面半徑Rr=149.8 mm,槽開口寬度角βoa=1.39°,極弧系數(shù)αp=0.7,并聯(lián)支路數(shù)為16,初始位置角θ0=5.625°,節(jié)距為1,每相匝數(shù)為523,額定功率為10 kW,額定轉(zhuǎn)矩為160 N·m。在MATLAB軟件中進(jìn)行編程求解析解時,諧波階次分別取:k=400,m=5,n=10,x=5(開輔助槽時)。
3.1 氣隙子域的磁通密度分布
根據(jù)式(20)可求得徑向磁通密度
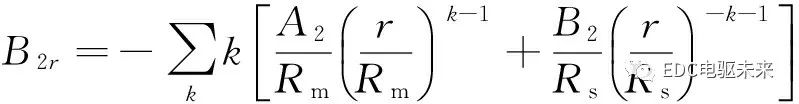 sin(kθ)+
sin(kθ)+
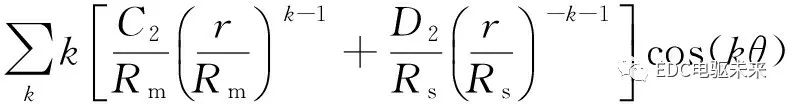
(28)
切向磁通密度
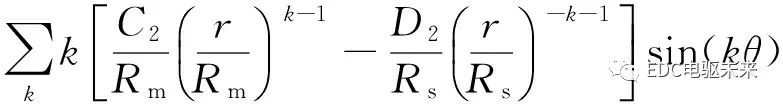
(29)
將通過分界面條件求解得到的氣隙子域的諧波系數(shù)A2、B2、C2、D2代入式(28)和(29),得
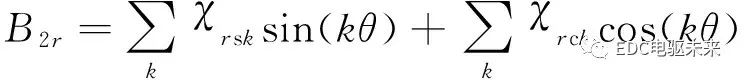
(30)
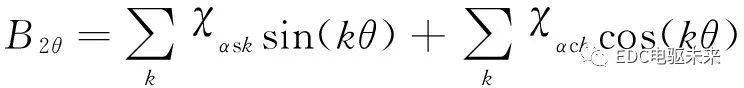
(31)
式中:χrsk、χrck、χαsk、χαck是半徑為r的圓周上氣隙磁通密度徑向和切向分量的各次諧波幅值。
圖2為電機(jī)空載時氣隙中心位置r=(Rm+Rs)/2處的徑向、切向磁通密度的解析解與有限元解,從中可以看出,解析解與有限元解吻合良好,驗(yàn)證了解析模型的有效性和精確性。
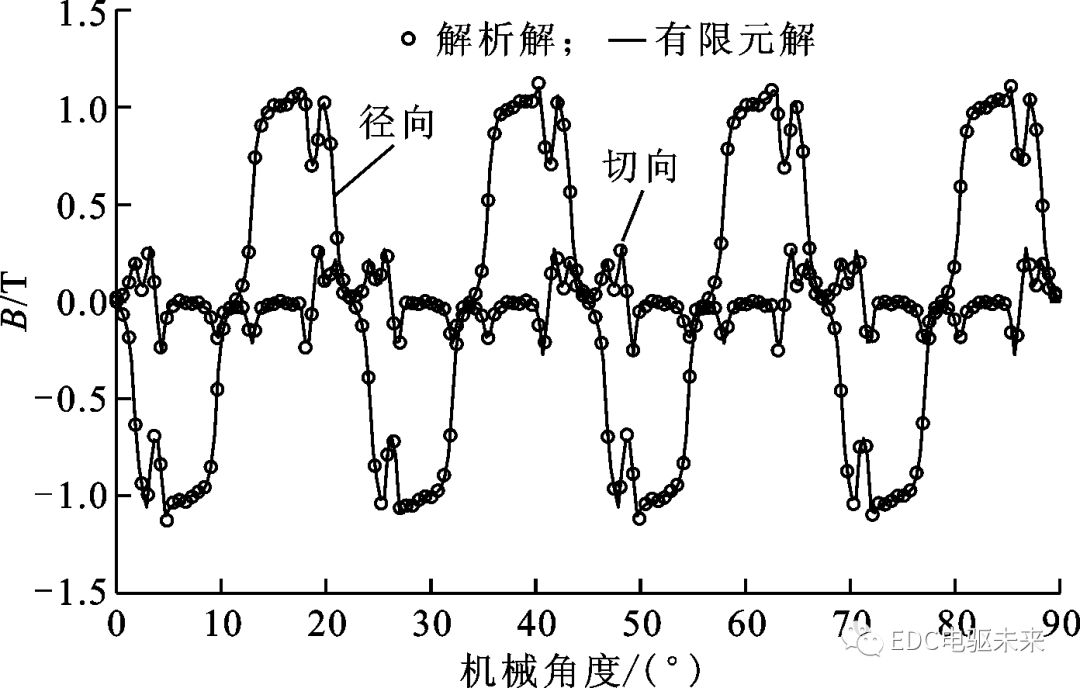
圖2 磁通密度有限元解和解析解的對比
3.2 反電動勢
假設(shè)電樞槽中的繞組均勻分布,由于每個槽中左、右放置了2個線圈邊,則2個線圈邊的磁鏈計(jì)算公式為
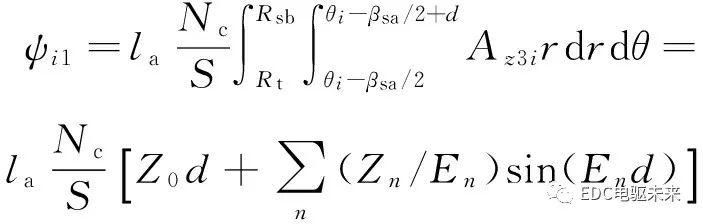
(32)
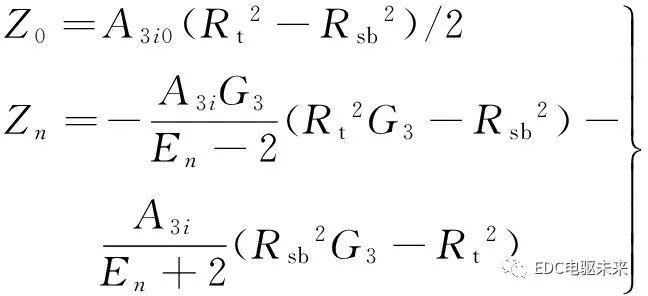
(33)
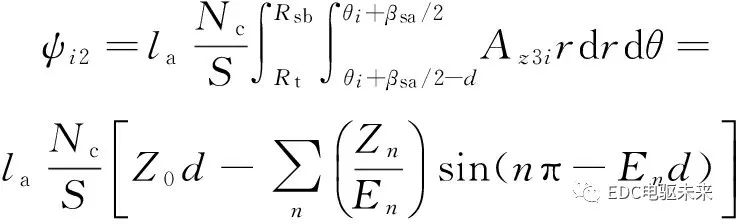
(34)
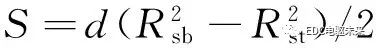
(35)
式中:Nc為線圈的匝數(shù);S為電樞槽內(nèi)一個線圈邊的面積;d為每個線圈邊所占的周向弧度。
三相繞組線圈在槽中的分布可定義為矩陣

(36)
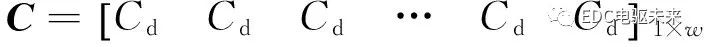
(37)
式中:C為電機(jī)的繞組分布矩陣;w為單元電機(jī)數(shù)。
所以,每相的總磁鏈為
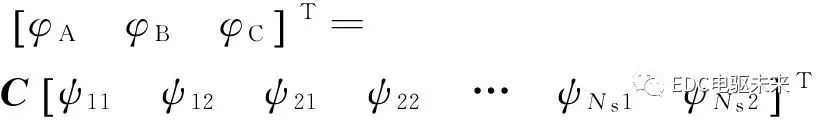
(38)
反電勢為
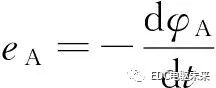
(39)
圖3和圖4分別為電機(jī)在額定轉(zhuǎn)速為600 r/min時C相的空載磁鏈和空載反電動勢變化,解析解與有限元解同樣吻合得較好,進(jìn)一步證明了本文解析模型的有效性和精確性。
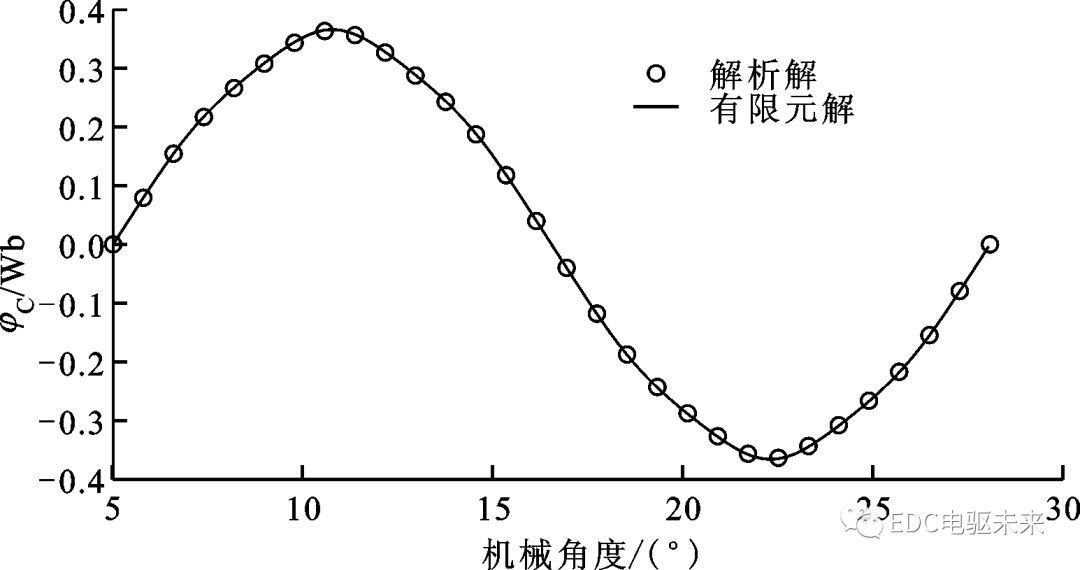
圖3 電機(jī)轉(zhuǎn)速為600 r/min時的空載C相磁鏈變化
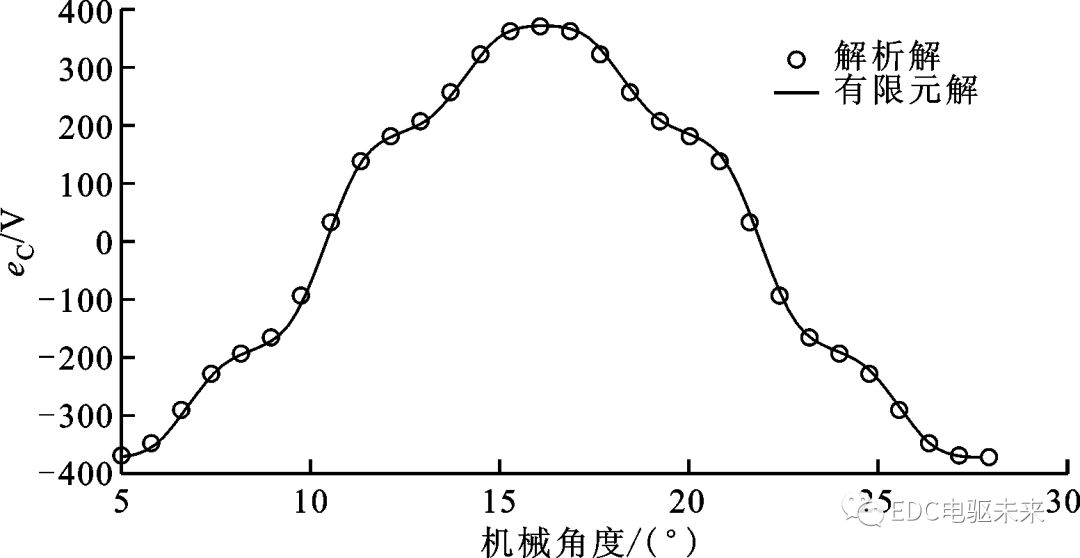
圖4 電機(jī)轉(zhuǎn)速為600 r/min時的空載C相反電動勢變化
3.3 齒槽轉(zhuǎn)矩
齒槽轉(zhuǎn)矩由永磁體和電樞鐵芯之間的相互作用產(chǎn)生。采用麥克斯韋張量法計(jì)算齒槽轉(zhuǎn)矩,取氣隙子域中心位置處的圓周為積分路徑
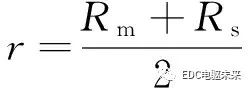
(40)
齒槽轉(zhuǎn)矩表達(dá)式為
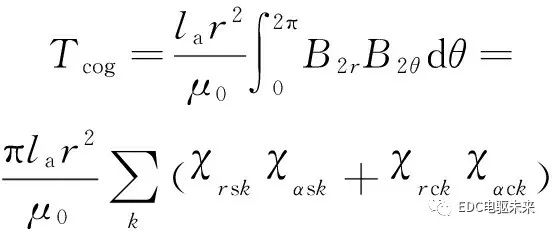
(41)
式中:la為電機(jī)的軸向長度。
由式(41)可知:精確的氣隙磁通密度是精確計(jì)算齒槽轉(zhuǎn)矩的關(guān)鍵;只有氣隙磁通密度的徑向和切向分量中的同階次的諧波相互作用才能產(chǎn)生齒槽轉(zhuǎn)矩。
圖5所示為齒槽轉(zhuǎn)矩在1個周期內(nèi)的解析解、有限元解及實(shí)驗(yàn)結(jié)果的對比,可見三者的吻合程度較高,再次證明了解析模型的有效性和精確性。圖5中的齒槽轉(zhuǎn)矩實(shí)驗(yàn)值是在測試系統(tǒng)將轉(zhuǎn)速控制為2 r/min時,由扭矩轉(zhuǎn)速測量儀測得的。
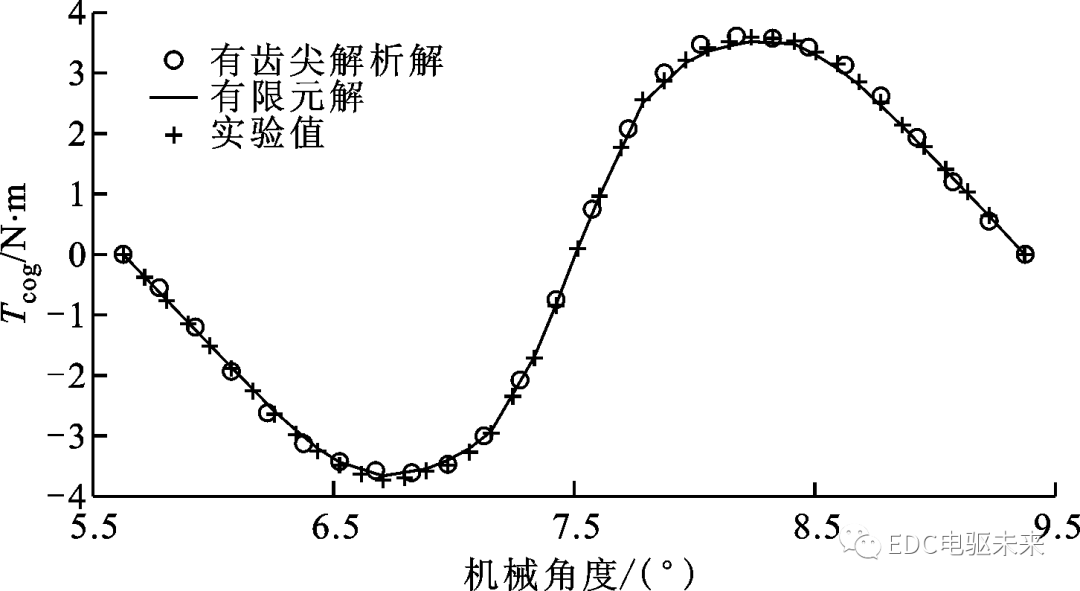
圖5 電機(jī)轉(zhuǎn)速為2 r/min時的齒槽轉(zhuǎn)矩
4 齒槽轉(zhuǎn)矩的削弱
前面計(jì)算了永磁電機(jī)的空載性能,證明本文的解析模型有效且精度較高。因此,下面基于該解析模型對電機(jī)的齒槽轉(zhuǎn)矩進(jìn)行優(yōu)化。
4.1 輔助槽寬度和深度對齒槽轉(zhuǎn)矩的影響
研究發(fā)現(xiàn),定子齒上開1、3、4或5個輔助槽均不能降低齒槽轉(zhuǎn)矩,只有開2個輔助槽時能夠削弱齒槽轉(zhuǎn)矩。本文的解析模型也可用于研究設(shè)置任意位置和數(shù)量的輔助槽。圖6所示為在定子齒上均勻?qū)ΨQ開有2個輔助槽(即dij=±2.82°)時,齒槽轉(zhuǎn)矩峰值隨輔助槽寬度和深度的變化。從圖中可以看出,齒槽轉(zhuǎn)矩峰值幾乎不隨輔助槽深度而變化,當(dāng)輔助槽寬度與電樞槽開口寬度的比值為0.6時齒槽轉(zhuǎn)矩最小,為3.025 N·m,相比不開輔助槽時的齒槽轉(zhuǎn)矩峰值3.6 N·m減小了16.6%。
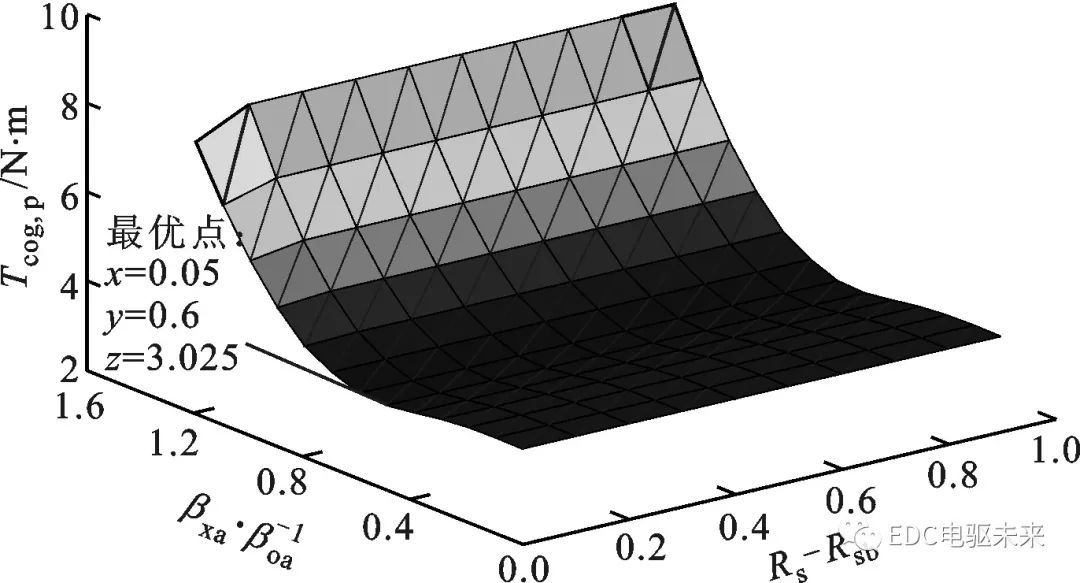
圖6 解析預(yù)測的輔助槽寬和槽深對齒槽轉(zhuǎn)矩峰值的影響
4.2 極弧系數(shù)和電樞槽開口寬度對齒槽轉(zhuǎn)矩的影響
圖7所示為不開輔助槽時齒槽轉(zhuǎn)矩峰值隨極弧系數(shù)和電樞槽開口寬度的變化,從中可以清晰地看出:當(dāng)極弧系數(shù)確定時,齒槽轉(zhuǎn)矩峰值基本上都是隨著電樞槽開口寬度的增加而變大,只有當(dāng)極弧系數(shù)為0.75時,趨勢才是相反的;當(dāng)極弧系數(shù)為0.7、電樞槽開口寬度為0.02 rad時,齒槽轉(zhuǎn)矩最小,為2.851 N·m。
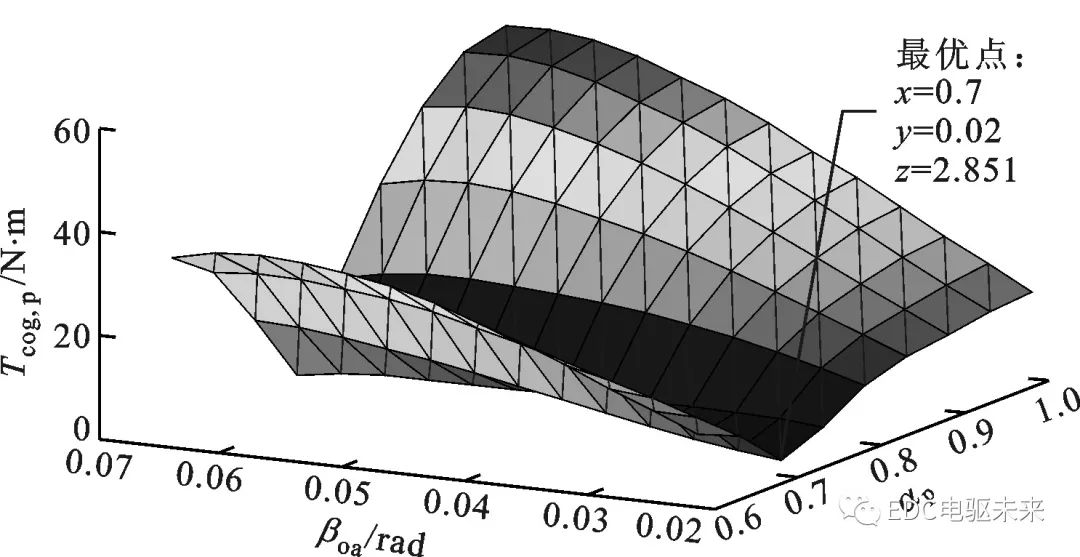
圖7 解析預(yù)測的極弧系數(shù)和電樞槽開口寬度對齒槽轉(zhuǎn)矩峰值的影響
4.3 最優(yōu)點(diǎn)驗(yàn)證
根據(jù)以上利用解析模型得到的電機(jī)各參數(shù)的最優(yōu)值進(jìn)行解析計(jì)算,并利用有限元法進(jìn)行驗(yàn)證。
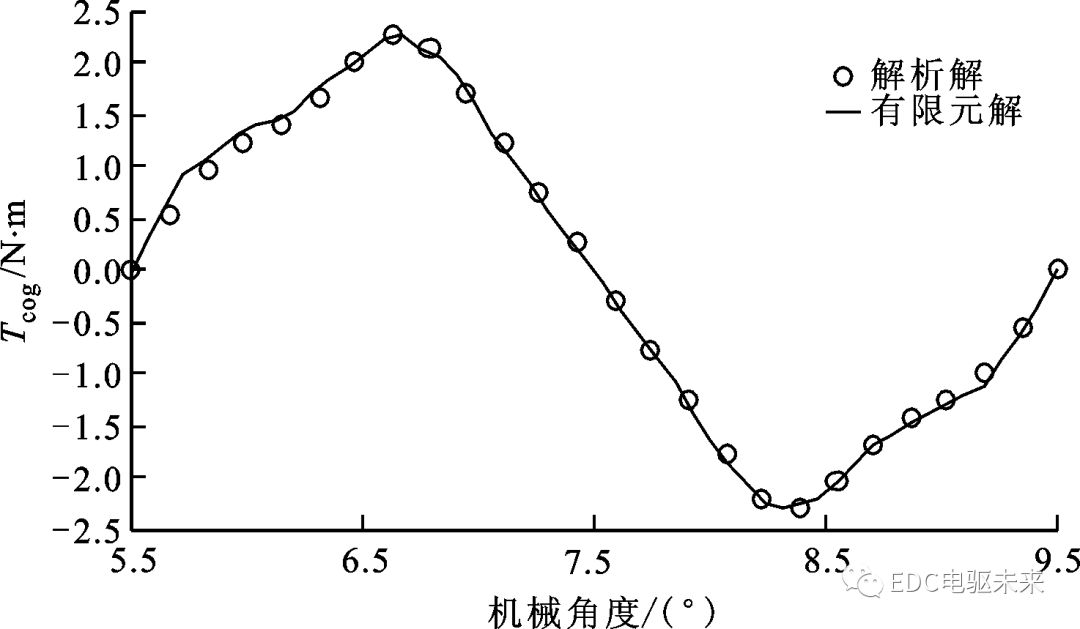
圖8 電機(jī)轉(zhuǎn)速為2 r/min時的齒槽轉(zhuǎn)矩
圖8為優(yōu)化后的齒槽轉(zhuǎn)矩,從中可以看出,優(yōu)化后的齒槽轉(zhuǎn)矩峰值為2.26 N·m,相比優(yōu)化前的3.6 N·m降低了37.2%。圖9為優(yōu)化后的開有2個輔助槽時的氣隙磁通密度分布,與圖2相比,輔助槽尺寸、極弧系數(shù)和槽開口寬度的改變對磁通密度的影響并不大,但是可以有效削弱齒槽轉(zhuǎn)矩,說明基于本文解析模型的永磁電機(jī)齒槽轉(zhuǎn)矩優(yōu)化合理有效。由圖8和圖9可知,解析解與有限元解高度吻合,證明本文提出的帶輔助槽永磁電機(jī)解析模型是精確和有效的。
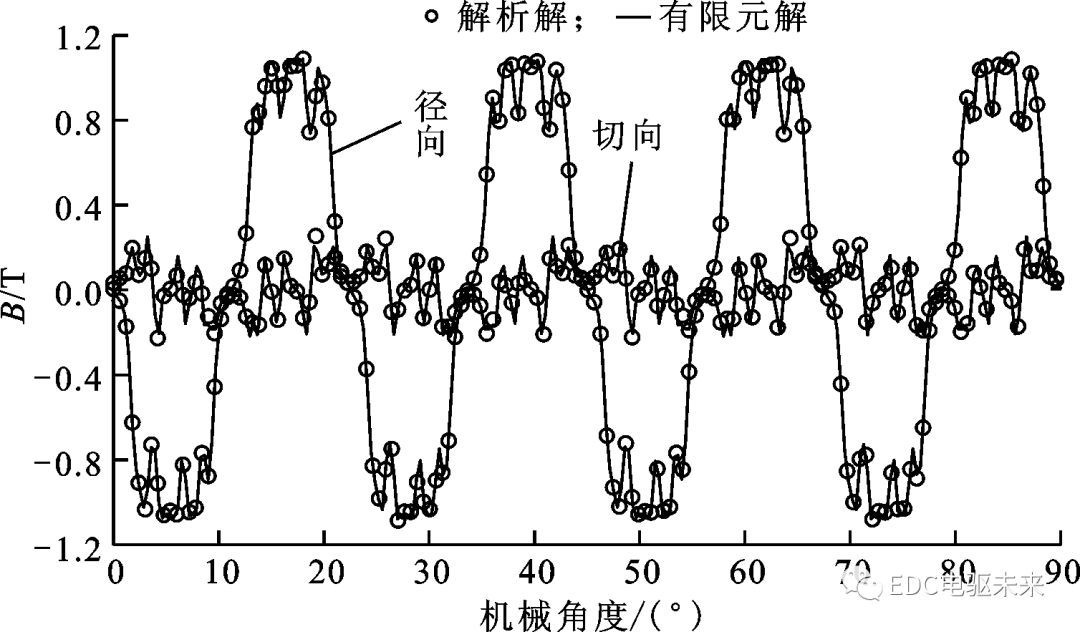
圖9 有限元法和解析法預(yù)測的氣隙磁通密度波形
5 結(jié)束語
本文在二維極坐標(biāo)下建立了一個定子齒上開有輔助槽的表貼式永磁電機(jī)的解析模型,考慮了電機(jī)的不同充磁方式、不同極槽配合和內(nèi)、外轉(zhuǎn)子結(jié)構(gòu);以一臺表貼式外轉(zhuǎn)子輪轂永磁電機(jī)為研究對象,計(jì)算了該電機(jī)的空載氣隙磁通密度分布、齒槽轉(zhuǎn)矩、磁鏈和反電動勢,并通過有限元法和齒槽轉(zhuǎn)矩實(shí)驗(yàn)驗(yàn)證了該解析模型的有效性和精確性;基于解析模型對影響該電機(jī)齒槽轉(zhuǎn)矩的相關(guān)參數(shù)進(jìn)行了研究和優(yōu)化。最后,以優(yōu)化后的參數(shù)對該電機(jī)的空載氣隙磁通密度和齒槽轉(zhuǎn)矩進(jìn)行了解析計(jì)算和有限元計(jì)算,兩者的計(jì)算結(jié)果高度吻合,而且有效削弱了齒槽轉(zhuǎn)矩,進(jìn)一步證明了本文所建立的解析模型的精確性和有效性。該模型不僅計(jì)算快、精度高,而且便于通過改變參數(shù)來研究電機(jī)的性能,有望為表貼式永磁電機(jī)的優(yōu)化與設(shè)計(jì)提供一種便捷的工具。
審核編輯:湯梓紅
-
永磁電機(jī)
+關(guān)注
關(guān)注
5文章
349瀏覽量
25659 -
模型
+關(guān)注
關(guān)注
1文章
3527瀏覽量
50495 -
輪轂電機(jī)
+關(guān)注
關(guān)注
3文章
54瀏覽量
13696
原文標(biāo)題:車用永磁輪轂電機(jī)解析建模與齒槽轉(zhuǎn)矩削弱
文章出處:【微信號:EDC電驅(qū)未來,微信公眾號:EDC電驅(qū)未來】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
新型稀土永磁材料與永磁電機(jī)
經(jīng)典永磁電機(jī)磁場文獻(xiàn)
復(fù)合結(jié)構(gòu)永磁電機(jī)
電動車的稀土永磁電機(jī)詳解
永磁電機(jī)的缺點(diǎn)辨析
車用電機(jī)系列——永磁電機(jī)技術(shù)及設(shè)計(jì)方案
如何保持永磁電機(jī)正常工作?
表貼式高速永磁電機(jī)多場耦合轉(zhuǎn)子設(shè)計(jì)_吳震宇
定子開槽表貼式永磁電機(jī)轉(zhuǎn)子偏心空載氣隙磁場全局解析法_李琛
永磁電機(jī)省電嗎_永磁電機(jī)省電的原因是什么




















評論