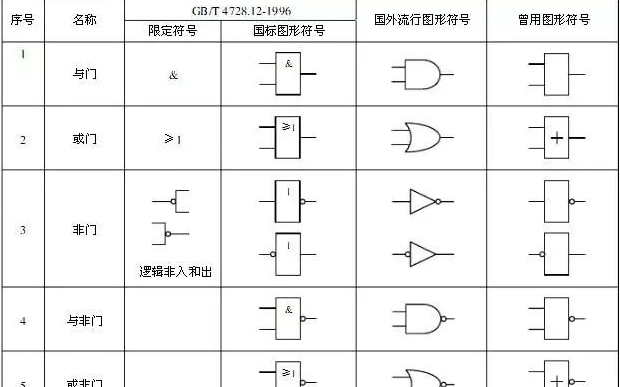
2.1. 數字邏輯
布爾對傳統邏輯學進行數字化,創立一門新的學科:邏輯代數(人們習慣成為布爾代數)。在布爾代數里,用字母來表示一個命題,用1代表命題為真,0代表命題為假。如果A命題是真的,則
A = 1
否則
A = 0
在邏輯學中,如果各個支命題是并列關系,稱為“聯言命題”,通常用“而且”來連接。為了表示這種邏輯關系,布爾代數使用“×”這個符號。這樣,一個聯言命題可以表示成:
A × B
為了方便也寫成 A ? B 或者簡化成 AB。
如果支命題都為假,推理結果是假,表示為: A × B = 0 × 0 = 0
如果支命題不全為假,推理結果是假,表示為:A × B = 0 × 1 = 1 × 0 = 0
如果支命題都真,推理結果為真,表示為:A × B = 1 × 1 = 1
表 2-1 聯言命題的真值表
| A | B | A × B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
在邏輯學中,如果各個支命題用“或者”“要么”來連接一種選擇關系,稱為“選言命題”。為了表示這種邏輯關系,布爾代數使用“+”這個符號。這樣,一個聯言命題可以表示成:
A + B
如果支命題都為假,推理結果是假,表示為: A + B = 0 + 0 = 0
如果支命題不全為假,推理結果是真,表示為:A + B = 0 + 1 = 1 + 0 = 1
如果支命題都真,推理結果為真,表示為A + B = 1 + 1 = 1
表 2-2 選言命題的真值表
| A | B | A + B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
除此之外的第三種邏輯關系是“非”,任何命題,比如命題A,不管是真是假,它的對立面是“非A”,可以表示成 。顯然, 如果,則;如果,則。
2.2. 邏輯電路
香農在1936年在其論文《繼電器和開關電路的符號化分析》中系統化的闡述了邏輯系統和電路通斷之間的關系。如果用X代表一個普通開關組成的電路,那么,X=1就表示開關合上;X=0表示開關打開,如圖 2-1(a)。
聯言命題演算相當于兩個開關X和Y的串聯,如圖 2-1(b)所示,只有當兩個開關都接通的時候,整個電路才是通的;兩個都斷開,或者其中任何一個斷開,整個電路是斷開的。選言命題演算相當于兩個開關的并聯,如圖 2-1(c)所示,兩個開關只要任何一個接通,或者兩個同時接通,整個電路就被接通;只有兩個開關同時斷開,整個電路才是斷開的。
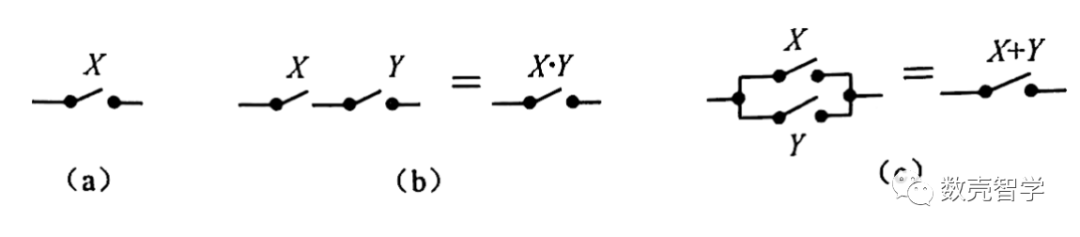
圖 2-1 命題演算和現實的開關組合具有一致性
按照這種觀點,布爾代數公式也有了新的解釋,見表 2-3。
| 布爾代數 | 對應的開關電路 |
|---|---|
| 0 · 0 = 0 | 一個斷開的開關和另一個斷開的開關串聯,整個電路還是斷開的 |
| 0 + 0 = 0 | 一個斷開的開關和另一個斷開的開關并聯,整個電路是斷開的 |
| 1 · 1 = 1 | 一個閉合的開關和另一個閉合的開關串聯,整個電路是連通的 |
| 1 + 1 = 1 | 一個閉合的開關和另一個閉合的開關并聯,整個電路是連通的 |
| 1 + 0 = 0 + 1 = 1 | 一個閉合的開關和另一個斷開的開關無論以什么順序并聯,整個電路都是連通的 |
| 1 ·0 = 0·1 = 0 | 一個閉合的開關和另一個斷開的開關無論以什么順序串聯,整個電路都是斷開的 |
表 2-3 布爾代數與開關電路的對應關系
2.3. 開關電路
上一節降到通過控制電路中的開關的閉合與斷開,可以控制電路的狀態(通電為1,不通電為0)來實現邏輯運算。但這里還有一個很大的問題,電路中的開關不能用手操作,如果用手去操作,邏輯電路就無法擴大規模和提高效率,不能實現自動化,不會有現代大規模集成電路的出現。幸好,我們找到一種用一個電路來控制另一個電路開關的方法,設計出”開關電路“。

圖 2-2 用開關電路組成一個報警系統
如圖 2-2所示的例子中,左邊是一個大型的機電設備,需要對其工作狀況進行監控,如果設備運行遇到故障,則及時報警。機電設備電路和報警器是兩個獨立的電路,可能兩個電路的運行電壓都不相同,開關電路盒子里面的設計需要做到左邊機電設備電路能控制右邊報警電路。
為了實現這樣的功能,我們在開關電路中引入“繼電器”。如圖 2-3是一個簡單的繼電器的例子,圖中開關、電源和被電線圍繞的電磁鐵組成電路A,當電路通電時,金屬柱具有磁吸功能,吸引“街鐵臂”向電磁鐵靠攏。可以想象,如果“街鐵臂”是另一個電路B中的開關觸頭的話,只要位置設計合理,可以達到電路B中的開關被閉合的效果。圖中電路A就是一個繼電器的原理圖。

圖 2-3繼電器的例子——摩爾斯電報示意圖
在明白了繼電器的原理之后,我們把圖 2-2中的開關電路部分的電路示意圖繪制出來(如圖 2-4)。通過一個繼電器裝置,使得機電設備的電路A能夠非接觸的控制報警電路B。

圖 2-4開關電路的內部邏輯——繼電器的應用
繼電器的引入實現開關電路的意義非常重大,從這以后,我們就能實現用一個電路控制另一個電路,“大規模集成電路群”也變得可能,這是現代化電子計算機出現的基礎。
2.4. 邏輯電路實現
在介紹完開關電路等知識的基礎上,我們終于可以介紹用電路實現“非”、“而且”、“或者”的邏輯運算。
2.4.1. 非門的實現
首先我們進一步把圖 2-4的圖簡化成示意圖(圖 2-5)。圖中當A電路中開關閉合(機電設備正常工作)的時候,繼電器J吸引F電路的開關打開,F電路的負載(喇叭)不工作;當A電路開關打開(機電設備異常造成電路無電流),繼電器J失去磁性,F電路的開關在彈簧裝置的作用下閉合,F電路復雜(喇叭)工作,發出警報。

圖 2-5用繼電器控制電路的示意圖
在這個例子中,F電路是輸出,A電路是輸入,發現F的狀態與A的狀態完全相反,這個電路設計實現了邏輯學中的“非”操作,這個電路邏輯用公式描述是:。
我們對電路的表現方式做進一步的簡化,使得在后面進一步解釋的時候更加簡介明了。

圖 2-6各個電路共用電源

圖 2-7 為了少繪制連線,使用“接地”符號
如果我們把圖 2-7中的陰影部分獨立出來,就是一個具有邏輯“非”操作的電子元件,成為“非門”。圖畫成圖 2-8:

圖 2-8非門的構造
在繪制電路圖的時候,非門用更簡單的符號表示(圖 2-9):

圖 2-9 非門的符號
非門實現了邏輯否定,即邏輯非:

2.4.2. 與門的實現
有了上面的基礎,我們可以很容易的看懂“與門”的電路結構圖(圖 2-10),輸出電路F有兩個開關分別對應A、B兩個輸入電路的繼電器J1、J2,當A電路通電時,J1對應的開關閉合,當B電路通電時,J2對應的開關閉合。因為F電路的兩個開關是串聯,所以只有當A、B電路同時通電(輸入1)的時候,F電路通電(輸出1)。發現F和A、B的邏輯關系如表 2-4。表達式是:F = A ? B
表 2-4 與門的輸入、輸出邏輯關系
| A | B | F |
|---|---|---|
| 斷開 (0) | 斷開 (0) | 斷開 (0) |
| 斷開 (0) | 通電(1) | 斷開 (0) |
| 通電(1) | 斷開 (0) | 斷開 (0) |
| 通電(1) | 通電(1) | 通電(1) |

圖 2-10 與門的簡化電路圖
與門在電路圖中簡化的畫法是:

圖 2-11 與門的符號
2.4.3. 或門的實現
“或門”的電路結構圖(圖 2-12),F電路是一個并聯電路,兩個開關處于并聯電路的兩個支路上,也就是說這兩個開關,至少有一個閉合,F電路就是通路。同上節所述,兩個開關分別由A、B電路的繼電器J1、J2控制,則,F和A、B的邏輯關系如表 2-5。表達式是:F = A + B 。
表 2-5 或門的邏輯輸入、輸出邏輯關系表
| A | B | F |
|---|---|---|
| 斷開 (0) | 斷開 (0) | 斷開 (0) |
| 斷開 (0) | 通電(1) | 通電(1) |
| 通電(1) | 斷開 (0) | 通電(1) |
| 通電(1) | 通電(1) | 通電(1) |

圖 2-12 或門的簡化電路圖
或門在電路圖中簡化的畫法是:

圖 2-13 或門的符號
2.5. 常用邏輯芯片介紹
2.5.1. 非門芯片XL74LS04

圖 2-14六路非門芯片針腳原理圖
2.5.2. 與門芯片XL74LS11

圖 2-15三路3輸入與門芯片針腳原理圖
2.5.3. 或門芯片CD7042BM96

圖 2-16二路4輸入或門芯片針腳原理圖
2.6. 小節
本章主要介紹了電路如何進行邏輯運算,從數字邏輯的布爾代數講到用電路如何實現簡單的邏輯運算,并最終闡述了“非”、“與”、“或”、“異或”四個基礎邏輯運算,設計了非門、與門、或門、異或門四個基礎電路。在此預告這幾個門的重要性,后面復雜的集成電路或者芯片的設計,幾乎都是由此類簡單的門電路來實現。
-
繼電器
+關注
關注
132文章
5333瀏覽量
148818 -
電路圖
+關注
關注
10340文章
10720瀏覽量
530252 -
開關電路
+關注
關注
58文章
553瀏覽量
66396 -
邏輯電路
+關注
關注
13文章
494瀏覽量
42611 -
非門
+關注
關注
1文章
32瀏覽量
33886
發布評論請先 登錄
相關推薦
單片機的邏輯運算符和位運算符是什么?數字電路中的常用符號
16進制字符串的邏輯運算問題
邏輯運算與移位指令
51單片機的算術和邏輯運算功能介紹
單片機邏輯電路與邏輯運算

verilog的邏輯運算符




 電路如何進行邏輯運算
電路如何進行邏輯運算
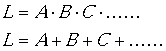











評論