1.1 什么是圖(graph)?
在圖論的上下文中,圖是一種結(jié)構(gòu)化數(shù)據(jù)類型,具有節(jié)點(diǎn)(nodes)(保存信息的實(shí)體)和邊緣(edges)(連接節(jié)點(diǎn)的連接,也可以保存信息)。
圖是一種數(shù)據(jù)結(jié)構(gòu)的方式,但它本身可以是一個(gè)數(shù)據(jù)點(diǎn)。圖是一種非歐幾里得數(shù)據(jù)類型,這意味著它們存在于三維空間,不像其他數(shù)據(jù)類型,比如圖像、文本和音頻。
圖可以具有某些屬性,這些屬性限制了可以對(duì)其執(zhí)行的可能操作和分析。這些屬性可以被定義。
1.2 圖的定義
首先,讓我們介紹一些定義。
在計(jì)算機(jī)科學(xué)中,我們經(jīng)常談?wù)撘环N稱為圖的數(shù)據(jù)結(jié)構(gòu):
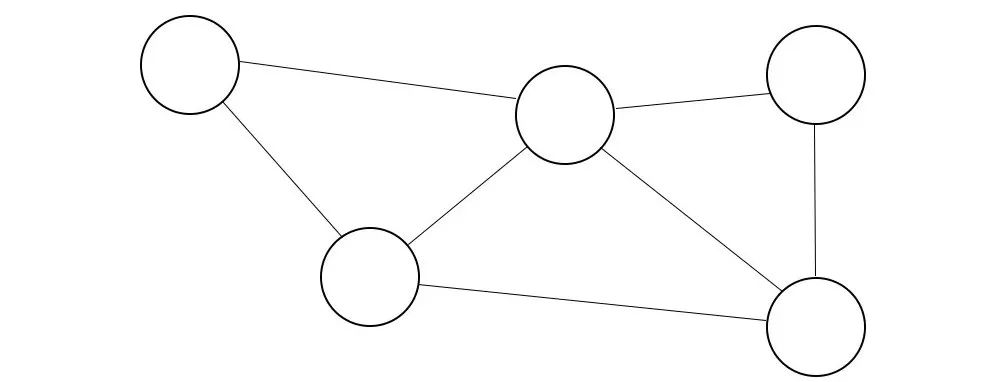
圖的邊緣和/或節(jié)點(diǎn)上可以有標(biāo)簽,讓我們給它一些邊緣和節(jié)點(diǎn)的標(biāo)簽。

標(biāo)簽也可以被視為權(quán)重,但這取決于圖的設(shè)計(jì)者。
標(biāo)簽不必是數(shù)字,它們可以是文本的。

標(biāo)簽不必是唯一的;給多個(gè)節(jié)點(diǎn)相同的標(biāo)簽是完全可能的,有時(shí)也是有用的。例如,氫分子就是一個(gè)例子:

注意混合了數(shù)值和文本數(shù)據(jù)類型
圖可以具有特征(也稱為屬性)。

要小心不要混淆特征和標(biāo)簽。一個(gè)簡(jiǎn)單的思考方式是使用名稱、角色和人的類比:
一個(gè)節(jié)點(diǎn)就是一個(gè)人,一個(gè)節(jié)點(diǎn)的標(biāo)簽就是一個(gè)人的名字,而節(jié)點(diǎn)的特征就是這個(gè)人的特點(diǎn)。
圖可以是有向的或無(wú)向的:

請(qǐng)注意,有向圖也可以具有無(wú)向邊
圖中的一個(gè)節(jié)點(diǎn)甚至可以有指向自身的邊緣。這被稱為自環(huán)(self-loop)。
圖可以是:
- 異構(gòu)的(Heterogeneous) — 由不同類型的節(jié)點(diǎn)組成
- 同構(gòu)的(Homogeneous) — 由相同類型的節(jié)點(diǎn)組成
并且可以是:
- 靜態(tài)的(Static) — 節(jié)點(diǎn)和邊不變,沒(méi)有添加或刪除
- 動(dòng)態(tài)的(Dynamic) — 節(jié)點(diǎn)和邊發(fā)生變化,添加、刪除、移動(dòng)等
粗略地說(shuō),圖可以模糊地描述為:
- 密集的(Dense) — 由許多節(jié)點(diǎn)和邊組成
- 稀疏的(Sparse) — 由較少的節(jié)點(diǎn)和邊組成
通過(guò)將它們轉(zhuǎn)化為平面形式,可以使圖看起來(lái)更整潔,這基本上意味著重新排列節(jié)點(diǎn),使邊不相交。

當(dāng)我們探索目前在各種GNN架構(gòu)中使用的許多不同方法時(shí),這些概念和術(shù)語(yǔ)將會(huì)派上用場(chǎng)。其中一些基本方法在以下方面進(jìn)行了描述:
1.3 圖分析
有各種不同的圖結(jié)構(gòu)可供ML模型學(xué)習(xí)(Wheel,Cycle,Star,Grid,Lollipop,Dense,Sparse等)。
你可以遍歷一個(gè)圖:

Jon在4個(gè)時(shí)間步驟內(nèi)從Bob到Bic;他最好希望不下雪!
在這種情況下,我們正在遍歷一個(gè)無(wú)向圖。顯然,如果圖是有向的,那么只需按照邊的方向前進(jìn)。有幾種不同類型的遍歷,所以要注意措辭。以下是一些最常見(jiàn)的圖遍歷術(shù)語(yǔ)及其含義:
- 行走(Walk):圖的遍歷 —— 閉合行走是指目標(biāo)節(jié)點(diǎn)與源節(jié)點(diǎn)相同
- 小徑(Trail):沒(méi)有重復(fù)邊的行走 —— 電路(Circuit)是閉合小徑
- 路徑(Path):沒(méi)有重復(fù)節(jié)點(diǎn)的行走 —— 循環(huán)(Cycle)是閉合路徑
在遍歷的概念基礎(chǔ)上,人們還可以在圖上發(fā)送消息。

Sam?更像是S-p-am(垃圾郵件)...
所有的Sam的鄰居都給他發(fā)送了一條消息,其中t代表時(shí)間步驟。Sam可以選擇打開(kāi)他的郵箱并更新自己的信息。在具有注意機(jī)制的模型中,信息在網(wǎng)絡(luò)中傳播的概念非常重要。在圖中,消息傳遞是我們泛化卷積的一種方式。稍后會(huì)詳細(xì)討論。
1.4 E-圖 — 計(jì)算機(jī)上的圖
通過(guò)學(xué)習(xí)所有這些,你現(xiàn)在對(duì)圖理論有了基本的理解!任何對(duì)GNNs重要的其他概念將會(huì)隨著它們的出現(xiàn)而進(jìn)行解釋,但與此同時(shí),還有一個(gè)關(guān)于圖的最后一個(gè)主題我們需要涵蓋。我們必須學(xué)會(huì)如何在計(jì)算中表達(dá)圖。
有幾種方法可以將圖轉(zhuǎn)化為計(jì)算機(jī)可以處理的格式;它們都是不同類型的矩陣。
關(guān)聯(lián)矩陣Incidence Matrix(I):
關(guān)聯(lián)矩陣通常在研究論文中用大寫字母I表示,由1、0和-1組成,關(guān)聯(lián)矩陣可以按照以下簡(jiǎn)單的模式制作:

從圖到關(guān)聯(lián)矩陣
(帶權(quán)重的)鄰接矩陣Adjacency Matrix(A):
圖的鄰接矩陣由1和0組成,除非它是加權(quán)或帶標(biāo)簽的。在任何情況下,A都可以按照以下規(guī)則構(gòu)建:

無(wú)向圖的鄰接矩陣因此在其對(duì)角線上是對(duì)稱的,從左上角對(duì)象到右下角:

有向圖的鄰接矩陣只覆蓋對(duì)角線線的一側(cè),因?yàn)橛邢驁D的邊只朝一個(gè)方向。
鄰接矩陣可以是“帶權(quán)重的”,這基本上意味著每條邊都有與之關(guān)聯(lián)的值,所以不是1,而是將值放在相應(yīng)的矩陣坐標(biāo)中。這些權(quán)重可以代表任何你想要的東西。例如,在分子的情況下,它們可以表示兩個(gè)節(jié)點(diǎn)(原子)之間的鍵的類型。在LinkedIn這樣的社交網(wǎng)絡(luò)中,它們可以表示兩個(gè)節(jié)點(diǎn)(人)之間的1st、2nd或3rd級(jí)連接。
邊的權(quán)重概念是使GNNs如此強(qiáng)大的一個(gè)屬性;它們?cè)试S我們考慮結(jié)構(gòu)性(依賴性)和獨(dú)立性信息。對(duì)于實(shí)際應(yīng)用,這意味著我們可以考慮外部和內(nèi)部信息。
度矩陣(D):
圖的度矩陣可以通過(guò)之前介紹的度概念來(lái)找到。D本質(zhì)上是一個(gè)對(duì)角矩陣,其中對(duì)角線的每個(gè)值都是其對(duì)應(yīng)節(jié)點(diǎn)的度數(shù)。

各種類型的圖和矩陣(由歐洲生物信息學(xué)研究所提供)
不要忘記度數(shù)只是鄰接矩陣的每一行的總和。然后,這些度數(shù)被放在矩陣的對(duì)角線上(鄰接矩陣的對(duì)稱線)。這很好地引出了最后的矩陣:
拉普拉斯矩陣(L):
圖的拉普拉斯矩陣是通過(guò)從鄰接矩陣中減去度矩陣而得到的:

度矩陣中的每個(gè)值都減去了相應(yīng)的鄰接矩陣中的值,如下所示:
 圖矩陣三合一(由維基百科提供)
圖矩陣三合一(由維基百科提供)
還有其他圖矩陣表示法,如關(guān)聯(lián)矩陣,但絕大多數(shù)應(yīng)用于圖類型數(shù)據(jù)的GNN應(yīng)用都使用這三個(gè)矩陣中的一個(gè)、兩個(gè)或全部。這是因?yàn)樗鼈儯绕涫抢绽咕仃嚕峁┝岁P(guān)于實(shí)體(具有屬性的元素)和關(guān)系(實(shí)體之間的連接)的重要信息。
唯一缺失的是一個(gè)規(guī)則(將實(shí)體通過(guò)關(guān)系映射到其他實(shí)體的函數(shù))。這就是神經(jīng)網(wǎng)絡(luò)派上用場(chǎng)的地方。
2. 深度學(xué)習(xí)
神經(jīng)網(wǎng)絡(luò)模型(或簡(jiǎn)稱NN)及其擴(kuò)展家族,包括卷積神經(jīng)網(wǎng)絡(luò)、循環(huán)神經(jīng)網(wǎng)絡(luò),當(dāng)然還有圖神經(jīng)網(wǎng)絡(luò),都是深度學(xué)習(xí)算法的一種類型。
深度學(xué)習(xí)是一種機(jī)器學(xué)習(xí)算法,而機(jī)器學(xué)習(xí)又是人工智能的一個(gè)子集。
一切都始于謙卑的線性方程。
如果我們將這個(gè)方程結(jié)構(gòu)化為一個(gè)感知器,我們可以看到:

其中輸出( )是偏差( )與輸入( )乘以權(quán)重( )的和( )。
神經(jīng)網(wǎng)絡(luò)通常具有激活函數(shù),它基本上決定了一個(gè)給定神經(jīng)元的輸出( )是否應(yīng)該被認(rèn)為是“激活的”,并將感知器的輸出值保持在一個(gè)合理的可計(jì)算范圍內(nèi)(例如,sigmoid函數(shù)用于 范圍,tanh函數(shù)用于 范圍,ReLU函數(shù)用于 或 等)。這就是為什么我們?cè)诟兄鞯哪┒烁郊蛹せ詈瘮?shù)的原因。

當(dāng)我們將一堆感知器放在一起時(shí),我們得到了一個(gè)類似于神經(jīng)網(wǎng)絡(luò)開(kāi)端的東西!這些感知器將數(shù)值值從一層傳遞到另一層,每一次傳遞都將該數(shù)值值接近網(wǎng)絡(luò)經(jīng)過(guò)訓(xùn)練的目標(biāo)/標(biāo)簽。

當(dāng)你把一堆感知器放在一起時(shí),你會(huì)得到:

一個(gè)普通的NN(由Digital Trends提供)
要訓(xùn)練神經(jīng)網(wǎng)絡(luò),我們首先需要計(jì)算我們需要調(diào)整模型權(quán)重的量。我們使用損失函數(shù)來(lái)做到這一點(diǎn),它計(jì)算誤差。
其中 是誤差, 是期望的輸出, 是實(shí)際輸出。在高層次上,誤差計(jì)算為實(shí)際輸出(神經(jīng)網(wǎng)絡(luò)的預(yù)測(cè))減去期望輸出(目標(biāo))。目標(biāo)是最小化誤差。通過(guò)使用稱為反向傳播的過(guò)程來(lái)調(diào)整每一層的權(quán)重來(lái)最小化誤差。
基本上,反向傳播將調(diào)整從輸出層傳播到輸入層的整個(gè)網(wǎng)絡(luò)。所調(diào)整的量由接收誤差作為輸入的優(yōu)化函數(shù)確定。優(yōu)化函數(shù)可以被想象成一個(gè)球在山上滾動(dòng),球的位置就是誤差。因此,當(dāng)球滾到山底時(shí),誤差達(dá)到最小值。
此外,還有一些必須定義的超參數(shù),其中最重要的之一是學(xué)習(xí)率。學(xué)習(xí)率調(diào)整了優(yōu)化函數(shù)應(yīng)用的速率。學(xué)習(xí)率就像重力設(shè)置;重力越大(學(xué)習(xí)率越高),球滾得越快,反之亦然。
神經(jīng)網(wǎng)絡(luò)具有許多不同的宏觀和微觀自定義選項(xiàng),使每個(gè)模型都具有獨(dú)特的特點(diǎn),性能各異,但它們都是基于這個(gè)基本模型的。稍后我們將看到,這對(duì)于圖學(xué)習(xí)尤其如此。根據(jù)需要將介紹卷積和重復(fù)等操作。
3. 深度神經(jīng)網(wǎng)絡(luò)就是一種圖
文章到此,你可能已經(jīng)注意到一個(gè)微妙但顯而易見(jiàn)的事實(shí):
神經(jīng)網(wǎng)絡(luò)實(shí)際上就是圖!
神經(jīng)網(wǎng)絡(luò)是一種特殊的圖,但它們具有相同的結(jié)構(gòu),因此具有相同的術(shù)語(yǔ)、概念和規(guī)則。
回想一下感知器的結(jié)構(gòu)本質(zhì)。我們可以將輸入值( )、偏差值( )和求和運(yùn)算( )視為圖中的3個(gè)節(jié)點(diǎn)。我們可以將權(quán)重( )視為連接輸入值( )和求和運(yùn)算( )的邊。
神經(jīng)網(wǎng)絡(luò)最相似的具體類型是多部分圖。多部分圖是可以分成不同節(jié)點(diǎn)集的圖。每個(gè)節(jié)點(diǎn)集中的節(jié)點(diǎn)可以在節(jié)點(diǎn)集之間共享邊,但不能在每個(gè)節(jié)點(diǎn)集內(nèi)部共享邊。

同構(gòu)二分圖(由Wolfram MathWorld提供)
有些神經(jīng)網(wǎng)絡(luò)甚至具有完全連接的節(jié)點(diǎn)、條件節(jié)點(diǎn)和其他瘋狂的架構(gòu),這些架構(gòu)賦予了神經(jīng)網(wǎng)絡(luò)其特有的多功能性和強(qiáng)大性能;以下是一些最流行的架構(gòu):

神經(jīng)網(wǎng)絡(luò)動(dòng)物園(由Asimov Institute提供)
每種顏色對(duì)應(yīng)于不同類型的節(jié)點(diǎn),可以以多種不同的方式排列。通過(guò)網(wǎng)絡(luò)中的數(shù)據(jù)前向或后向傳播類似于圖中的消息傳遞。圖中的邊緣或節(jié)點(diǎn)特征類似于神經(jīng)網(wǎng)絡(luò)中的權(quán)重。請(qǐng)注意,一些節(jié)點(diǎn)甚至具有我們之前提到的自環(huán)(RNNs — 循環(huán)神經(jīng)網(wǎng)絡(luò)中的特性)。
神經(jīng)網(wǎng)絡(luò)并不是唯一具有類似圖結(jié)構(gòu)的機(jī)器學(xué)習(xí)模型。
- K均值
- K最近鄰
- 決策樹
- 隨機(jī)森林
- 馬爾可夫鏈
如上模型,它們本身都具有圖形結(jié)構(gòu),或者以圖形結(jié)構(gòu)輸出數(shù)據(jù)。
4. 本質(zhì)上
我們涵蓋了很多內(nèi)容,但回顧一下,我們深入探討了3個(gè)概念:
- 圖論
- 深度學(xué)習(xí)
- 使用圖理論的機(jī)器學(xué)習(xí)
有了這些先決條件,人們可以充分理解和欣賞圖學(xué)習(xí)。在高層次上,圖學(xué)習(xí)進(jìn)一步探索并利用了深度學(xué)習(xí)和圖理論之間的關(guān)系,使用一系列設(shè)計(jì)用于處理非歐幾里德數(shù)據(jù)的神經(jīng)網(wǎng)絡(luò)。
5. 關(guān)鍵要點(diǎn)
有許多關(guān)鍵要點(diǎn),但要點(diǎn)是:
- 所有圖都具有定義其可用或可分析操作的屬性。
- 圖是使用各種矩陣來(lái)進(jìn)行計(jì)算表示的。每個(gè)矩陣提供不同數(shù)量或類型的信息。
- 深度學(xué)習(xí)是機(jī)器學(xué)習(xí)的一個(gè)子集,大致模擬人類大腦中神經(jīng)元工作的方式。
- 深度學(xué)習(xí)通過(guò)在網(wǎng)絡(luò)中前向傳遞信息并向后傳播神經(jīng)元調(diào)整來(lái)進(jìn)行迭代學(xué)習(xí)。
- 神經(jīng)網(wǎng)絡(luò)(以及其他機(jī)器學(xué)習(xí)算法)與圖理論有密切聯(lián)系;
現(xiàn)在你具備了深入了解圖學(xué)習(xí)的所有先決條件。一個(gè)好的起點(diǎn)是研究迄今為止已經(jīng)開(kāi)發(fā)的各種圖神經(jīng)網(wǎng)絡(luò)的種類。
-
音頻
+關(guān)注
關(guān)注
29文章
2881瀏覽量
81604 -
數(shù)據(jù)
+關(guān)注
關(guān)注
8文章
7064瀏覽量
89105 -
卷積
+關(guān)注
關(guān)注
0文章
95瀏覽量
18521 -
深度學(xué)習(xí)
+關(guān)注
關(guān)注
73文章
5504瀏覽量
121217
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
AI、5G和生物識(shí)別上榜 阿里巴巴達(dá)摩院發(fā)布2019十大科技趨勢(shì)
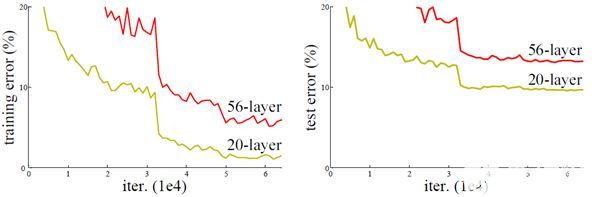
深度學(xué)習(xí)與圖神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)分享:CNN經(jīng)典網(wǎng)絡(luò)之-ResNet
Nanopi深度學(xué)習(xí)之路(1)深度學(xué)習(xí)框架分析
深度學(xué)習(xí)在汽車中的應(yīng)用
如何在交通領(lǐng)域構(gòu)建基于圖的深度學(xué)習(xí)架構(gòu)
深度學(xué)習(xí)存在哪些問(wèn)題?
深度學(xué)習(xí)模型是如何創(chuàng)建的?
什么是深度學(xué)習(xí)?使用FPGA進(jìn)行深度學(xué)習(xí)的好處?
深度學(xué)習(xí)是什么?了解深度學(xué)習(xí)難嗎?讓你快速了解深度學(xué)習(xí)的視頻講解
關(guān)系歸納偏差和深度學(xué)習(xí)及圖神經(jīng)網(wǎng)絡(luò)的詳細(xì)資料說(shuō)明

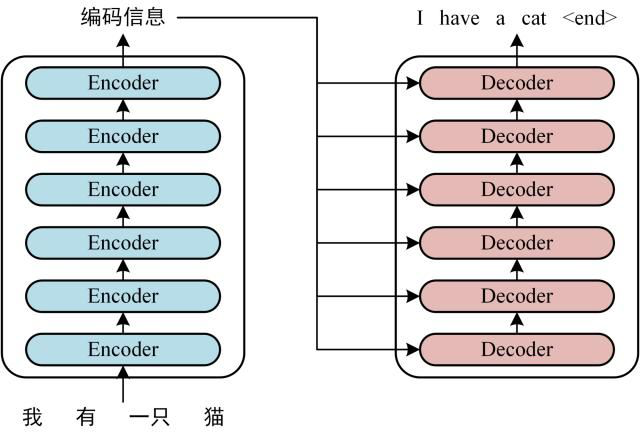
深度學(xué)習(xí)與圖神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)分享:Transformer




 深度學(xué)習(xí)的圖原理
深度學(xué)習(xí)的圖原理










評(píng)論