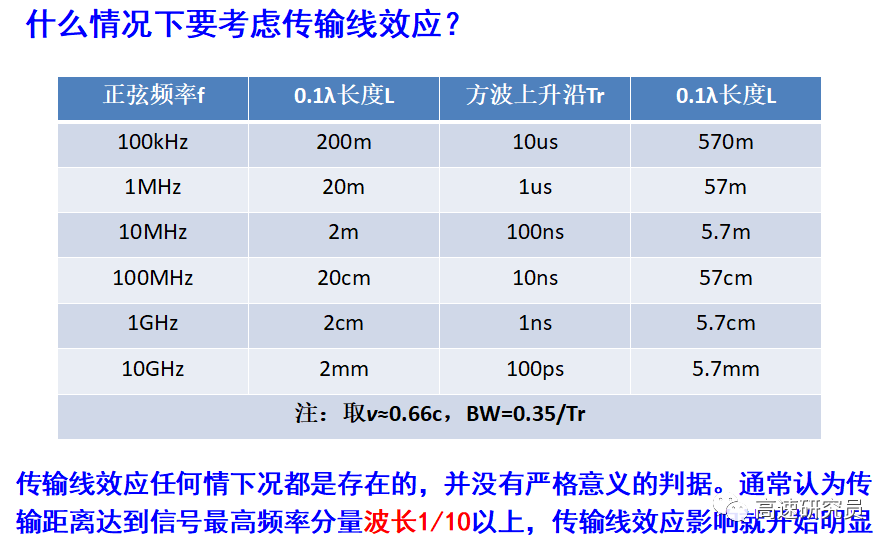
傳輸線匹配前提：開始考慮傳輸線效應，此時基爾霍夫電壓定律和基爾霍夫電流定律失效。

傳輸線對整個電路帶來以下效應：

1.反射信號。
2.延時和時序錯誤。
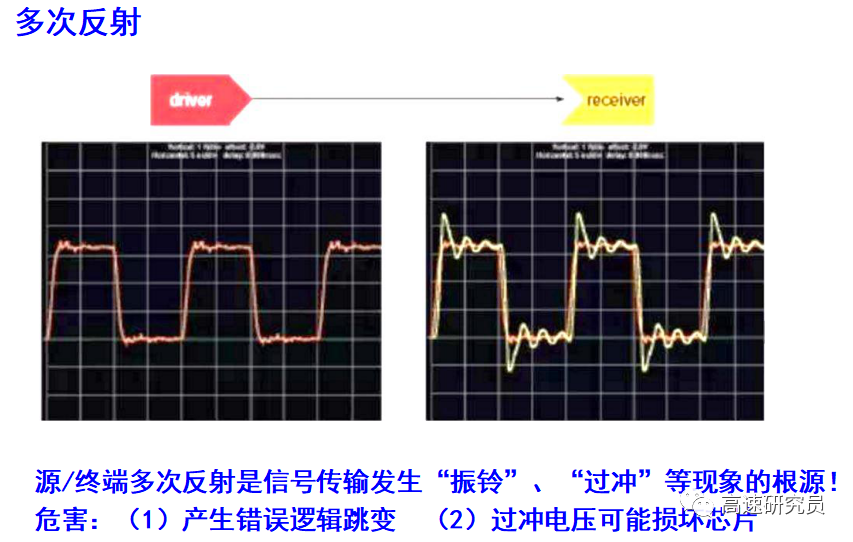
3.多次跨越邏輯電平門限錯誤。
4.過沖與下沖。
5.串擾。
6.電磁輻射。

一：傳輸線模型

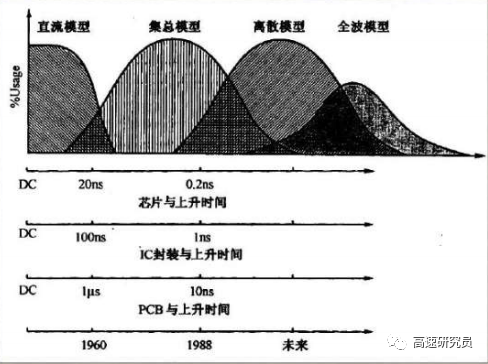
四種電性等效模型的分類與電磁波的波長（或信號的上升時間）相關，也與系統的幾何尺寸相關。

1.DC直流模型

只需要一個電阻或者零延遲時間的導線就足以代表電磁波的性能。

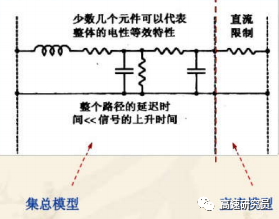
2.集總模型

如果傳輸線的整體傳輸延遲時間較信號的上升時間來的短的話，只需要一個RLC網絡或是RC網絡就可以代表整個電磁波的性能，我們稱它為“集總模型”。

在集總模型的環境里，電磁波的波長會遠大于電路的物理尺寸，所以，可以將分布的一些小的電路元件集總起來就可以精確地描述電磁波的性能。

3.RLC分布參數模型

一個導體系統（主要指無源網絡），若系統的物理尺寸足 夠小，以至于當信號輸入時，其上所有點同時達到相同的 電位，則該系統被稱為集中系統（ Lumped System）。反 之，則稱為分布系統（ Distributed System）。

簡化數學模型，用“電容”來描述電能。用“電感”來表示磁能，用“電阻”來代表轉換為熱的 能量損耗。這些元件被定義成沒有實際尺寸，由無損和無延遲的導線將它們連接起來。有了這些電路元件就不再需要麥克斯韋方程組和邊界條件，利用這些電路元件就可以來描述一個 所謂的理想傳輸線的結構。基本的傳輸線結構如圖所示，理想上，它是由無限多的RLC網絡所組成的，然而，為了計算的目的（特別是為了時域的計算方便），我們通常選擇有限個RLC網絡來代表。其基本的假設是每個 RLC網絡的延遲時間遠小于信號的波長或者上升時間。

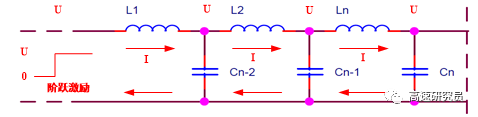
tr:上升時間，單位:（ps）。td:單位傳輸延遲時間，單位:（ps/in）

其物理意義: 上升時間在導體中傳輸時所占有的物理長度。

** 4.全波模型（RLGC全波模型)**

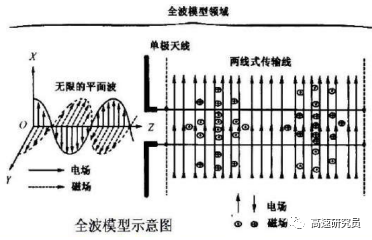
全波模型，理論來自于麥克斯韋方程式，假設電磁波在一個無限打大的平面上進行。X是電場的方向， Y是磁場的方向，整個電磁場往Z方向進行。傳播速度為光速。

阻抗，電場對磁場的比值，在自由空間里為377歐姆。當平面波遇到一個高傳導物體時，傳播方向會 隨即發生變化。如果適當地調整傳播的物體，則平面波可以被導入到一個傳輸線里，這個我們稱為全波模型。

使用選擇邊界條件用以代表實際物體的幾何結構以及所使用的材料來求解。全波模型的麥克斯威方程組，即使非常簡單的結構體，方程組也很難解出。

一：反射

是什么引起了反射？為什么信號遇到阻抗突變時會發生反射？

答案是：產生反射信號是為了滿足兩個重要的邊界條件。信號到達瞬時阻抗不同的兩個區域的交界面時，在信號/返回路徑的導體中僅存在一個電壓和一個電流回路。在交界面處，無論時從區域1還是從區域2看過去，在交界面的兩側的電壓和電流都必須相等。邊界處不可能出現電壓不連續，否則此處會產生一個無限大的電場；也不可能電流不連續，否則會在交界面處產生凈電荷。

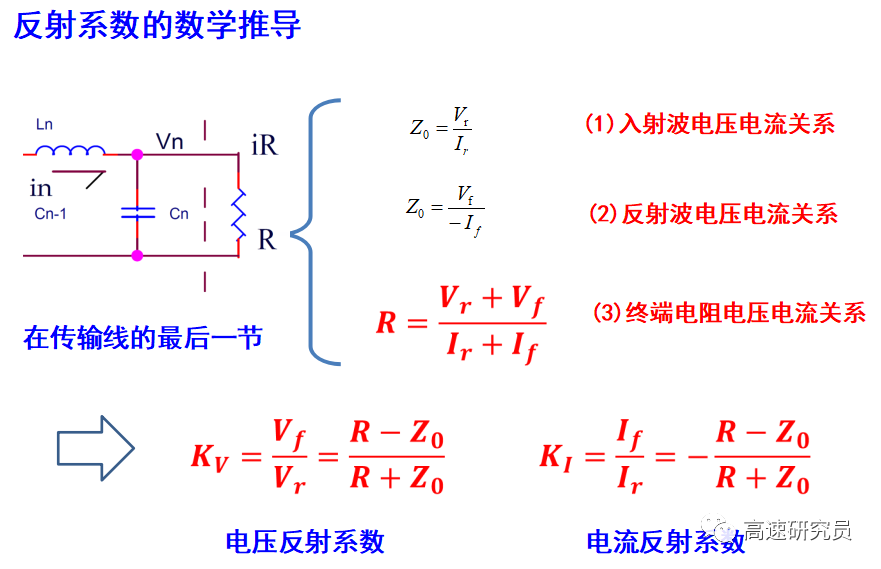
傳輸系數: t=2Z2/Z2+Z1

反射系數描述了反射回源端的那部分電壓，傳輸系數描述了通過交界面進入第二個區域的入射電壓。

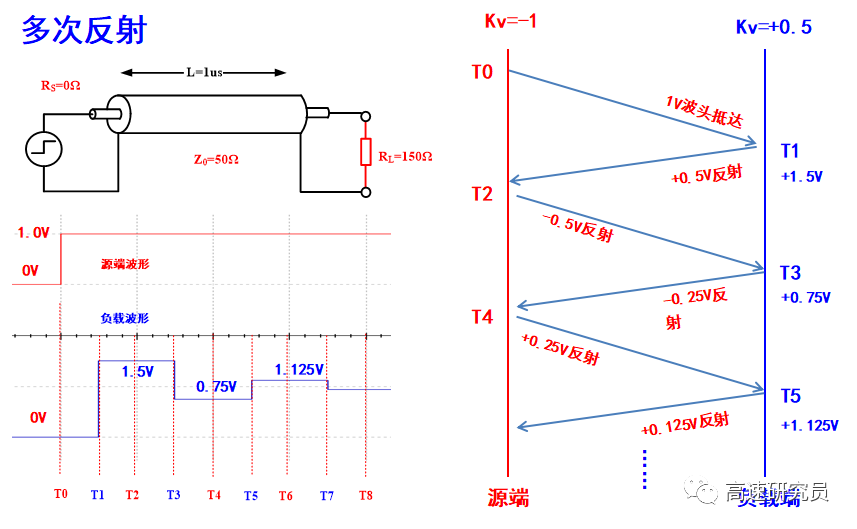
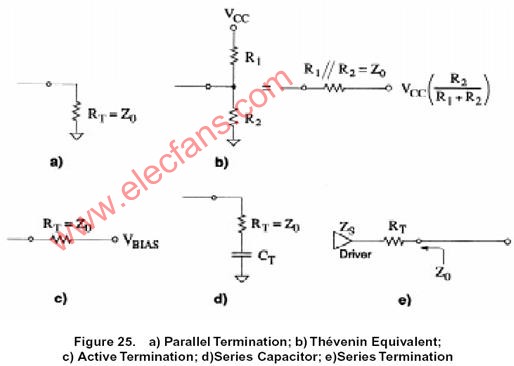
傳輸線的短接匹配有3種最重要的特殊情況：

首先：傳輸線的終端為開路

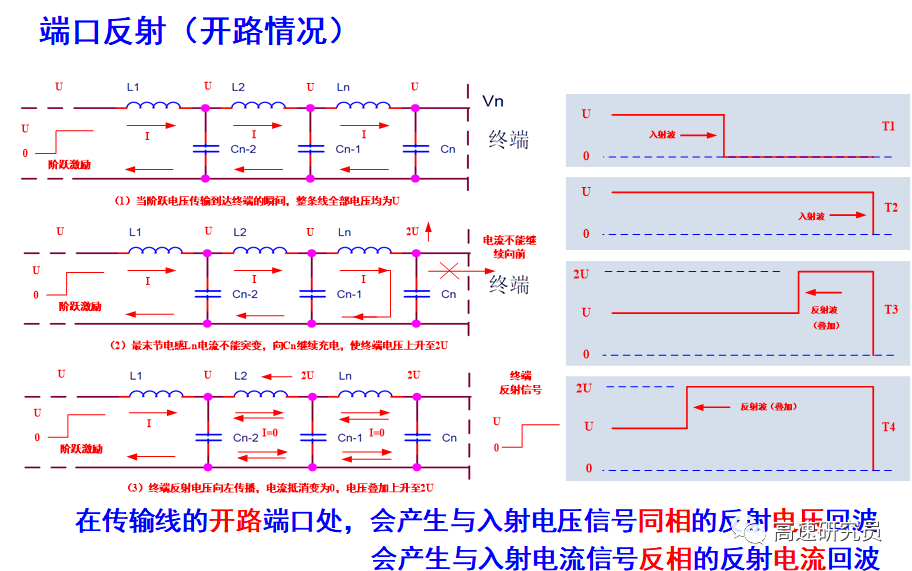
第二種特殊情況是：傳輸線的末端與返回路徑相短路，即末端阻抗為0。

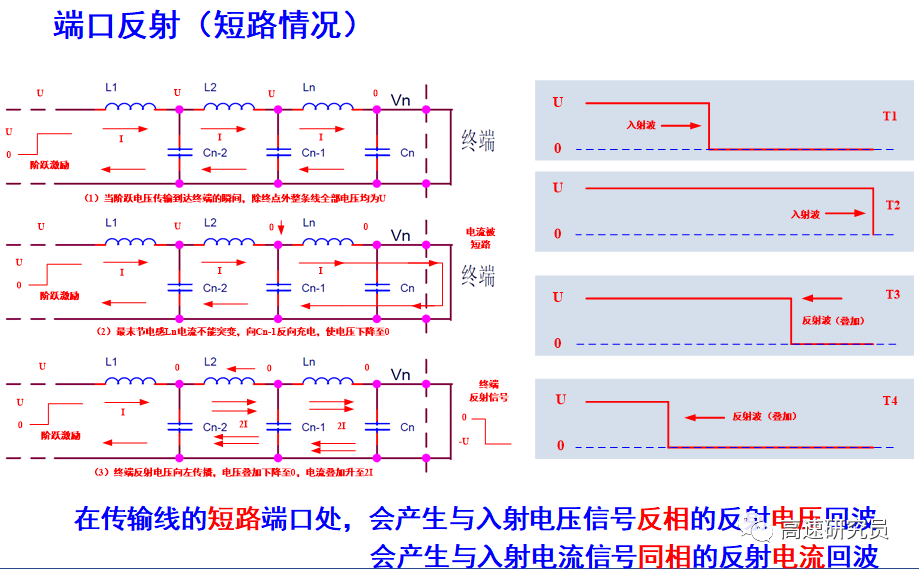
最后一種特殊情況是：傳輸線末端所接阻抗與傳輸線的特性阻抗相匹配。

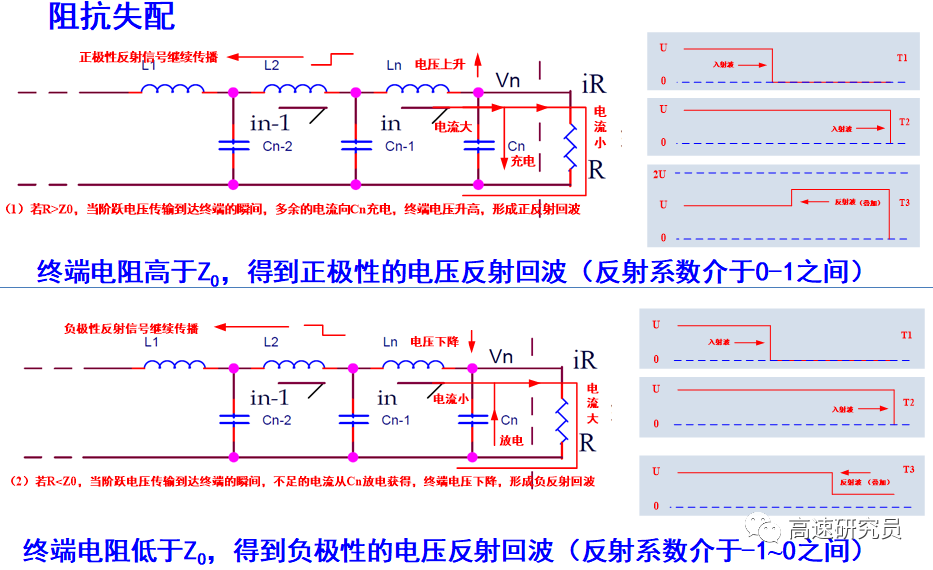
容性終端的反射與感性突變的反射：

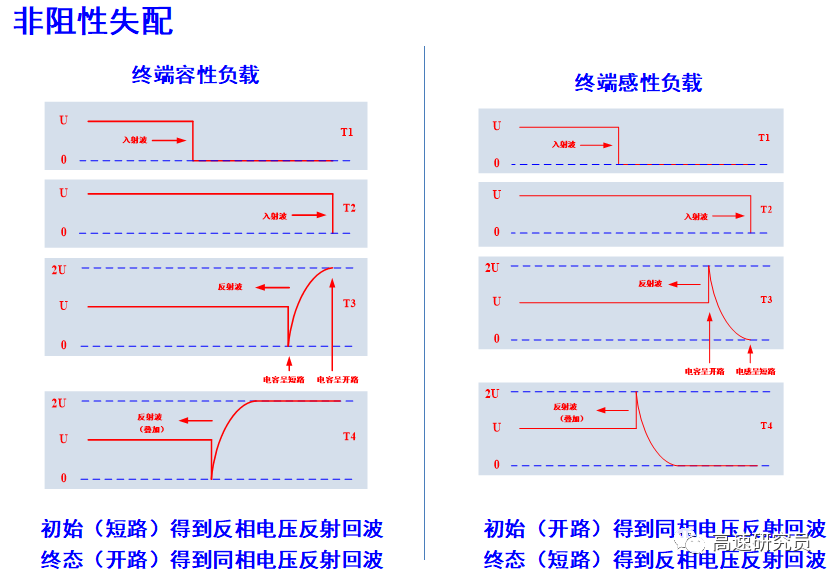
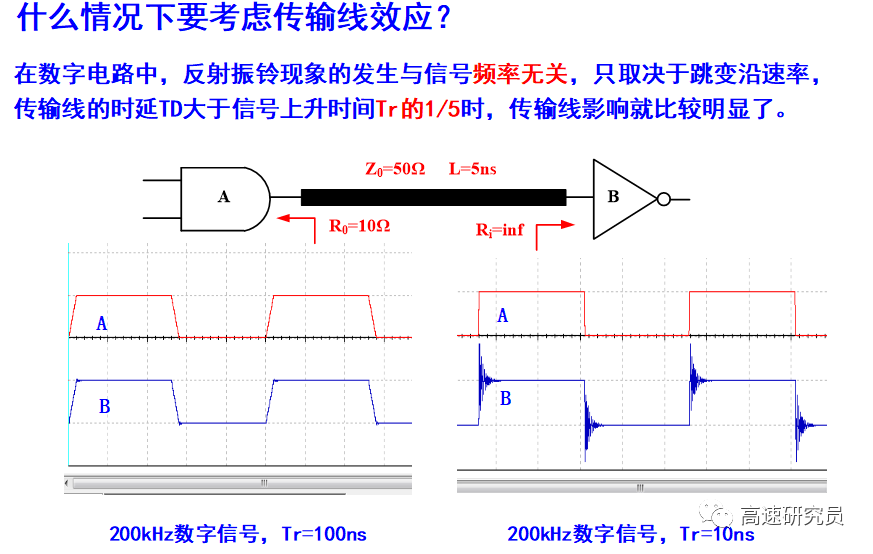
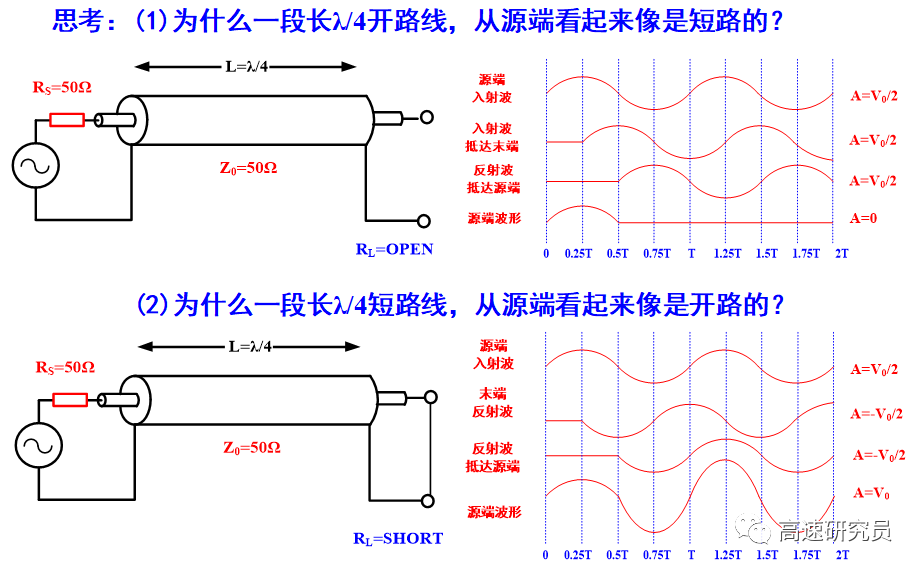
如果信號沿互聯傳播時受到的瞬時阻抗發生變化，則一部分信號將被反射，另一部分發生失真并繼續傳播下去，這一原理正是單一網絡中多數信號完整性產生的主要原因。

為了得到最優的信號質量，設計互聯的目的就是盡可能保持信號受到的阻抗恒定：

第一層含義：保持互聯的瞬時阻抗恒定。

** 第二層含義：可以在傳輸線的終端進行阻抗匹配。**

** 第三層含義：即使已經是可控阻抗互聯和終端連接，布線的拓撲結構也會影響反射，因此其中的一個策略是維持一個線性的布線拓撲，線上不要有分支。如果有分支則每個分支都要進行匹配。**

即使如此，信號遇到瞬時阻抗突變就會反射，這可能發生在線的末端，或者互聯拓撲結構發生改變的任何地方，如拐角、過孔、分支結構、連接件和封裝處。

沒有人知道到底是什么產生了反射電壓？只是知道這樣產生后，交界面兩側的電壓才可以相等，交界面處的電壓才是連續的。同樣，在交界面兩側也存在電流回路，電流也是連續的。這樣，系統才是平衡的。