引言:
在本文中,我們將深入探討機器人學的兩個核心概念:正運動學和逆運動學。這兩個概念是理解和控制機械臂運動的基礎。通過一個具體的7軸機械臂實例,我們將詳細介紹如何計算機械臂的正運動學和逆運動學。我們首先會解釋正運動學和逆運動學的基本概念和數學原理,然后我們將展示如何應用這些原理來計算7軸機械臂的運動。我們的目標是讓讀者對機械臂的運動控制有一個深入的理解,并了解如何在實踐中應用這些知識。
myArm 300
我們先來簡要介紹我們待會會使用到的機械臂myArm 300.
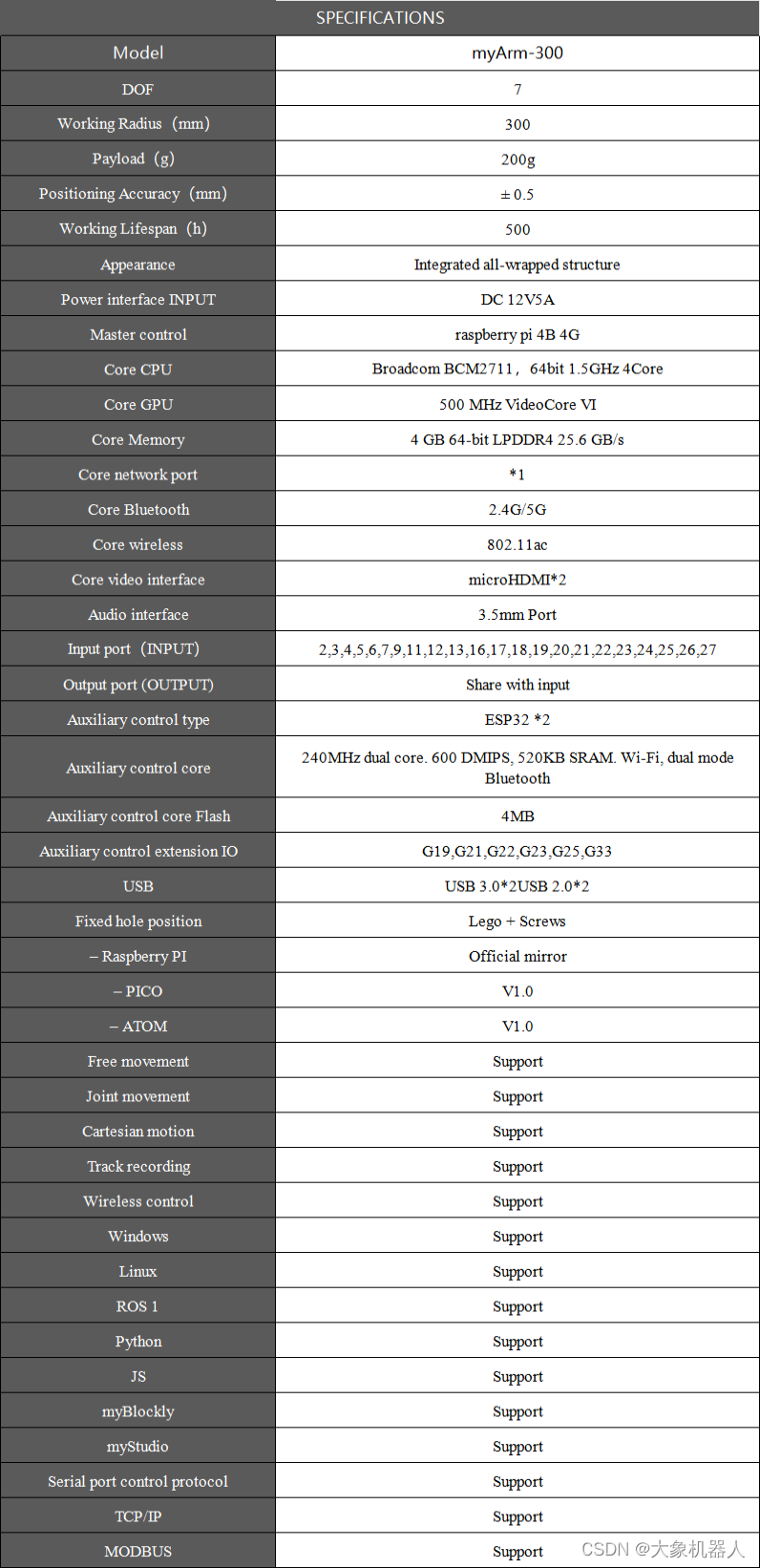
myArm 300 Pi是一塊全新的7自由度的中心對稱構型協作機械臂,myArm搭載著7個高精度的伺服電機,使得最大工作半徑300mm,末端最大負載成都能夠達到200g,重復定位精度最高達到了±0.5mm。

myArm 300 Pi的控制主板采用了樹莓派4B 4G,這是一種廣受歡迎的微型計算機,因其強大的性能和靈活的編程環境而備受贊譽。這意味著用戶可以使用多種編程語言來控制myArm 300 Pi,包括Python、C++、Java等,極大地提高了使用者的便利性和靈活性,它還支持ROS1/ROS2 在ROS操作系統中提供了許多功能,例如路徑規劃,避障,三維感知等。
基本概念
我們要想控制機械臂,就得有一套關于機械臂運動控制的算法。正逆運動學是其中的重要組成部分。在介紹正逆運動學之前,我們想先介紹DH模型,這個模型使得正逆運動學的計算變得更加直接和簡單。
DH模型
DH參數模型是機器人學中一種常用的描述機器人運動學的方法。它通過一組參數來描述機器人的關節連桿,從而方便地計算機器人末端執行器地位置和姿態。
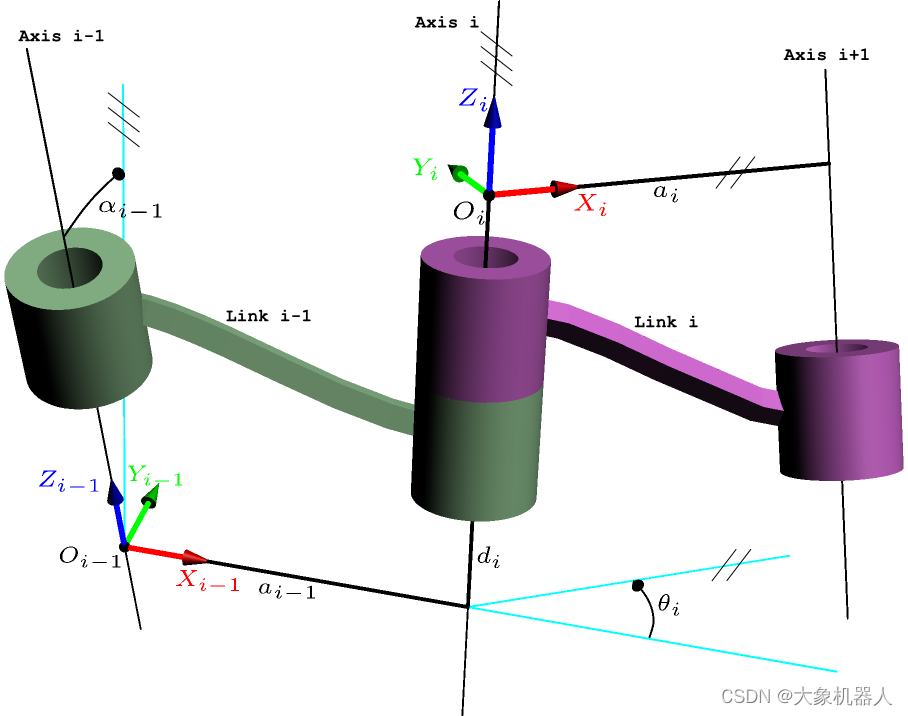
當使用DH模型用來描述機械臂時,我們將機械臂分解為一系列鏈接和關節,每個鏈接和關節都與一個坐標系相關聯。我們選擇一個基準坐標系,通常是機械臂的基座(底座)坐標系,然后,為每個鏈接和關節定義一個坐標系,我們定義兩個坐標系:前一個鏈接的坐標系和當前鏈接的坐標系。這兩個坐標系之間的變換由四個參數描述:
連桿長度(a):它表示相鄰鏈接之間的距離,沿著前一個鏈接的法線測量。它通常指的是鏈接的長度或者鏈接軸線的長度。
連桿的旋轉角度(α):它表示相鄰鏈接之間的旋轉角度,圍繞前一個鏈接的法線旋轉。它通常指的是鏈接軸線之間的旋轉。
關節的長度(d):它表示鏈接的長度或者關節的長度,沿著當前鏈接的法線測量。它通常指的是關節軸線的長度。
關節的旋轉角度(θ):它表示關節的旋轉角度,圍繞當前鏈接的法線旋轉。它通常指的是關節的角度或者關節的轉動。
通過組合這些參數,可以構建一個四維的變換矩陣,這個變換矩陣可以表示機械臂末端執行器的位置和姿態。
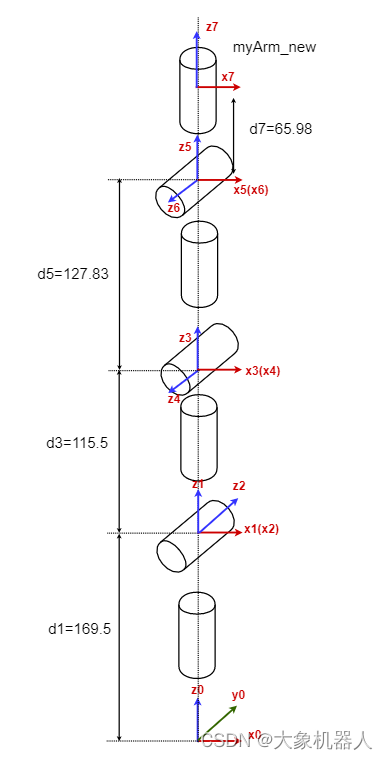
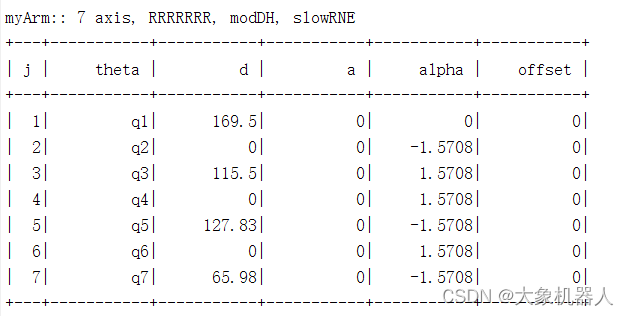
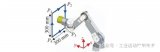
以myArm為例子,下圖是myArm 300 的DH模型圖以及SDH參數表。當我們有了一個機械臂的DH模型圖我們具體能干些什么呢:
正向運動學:通過給定關節角度,可以使用DH模型圖計算機械臂末端執行器的位置和姿態,從而進行路徑規劃和運動控制
逆向運動學:反過來,也可以用DH模型圖來解決逆向運動學問題,即給定目位置和姿態,計算出關節角度的變化,從而實現平滑的運動軌跡。
路徑規劃:給定一個開始位置和一個結束位置,可以使用DH模型來規劃機械臂的運動路徑。這可能涉及到解決一系列的逆運動學問題。
除此之外還有很多,比如說碰撞檢測和臂章,動畫和可視化機械臂,仿真機械臂等等。
正運動學
正運動學是用來描述機械臂從基座到末端執行器的位置和方向的計算方法。給定每個關節的角度,我們可以計算出機械臂末端的位置和方向。這是一個基于幾何和三角學的過程。
下面舉一個簡單的例子,在一個平面坐標系當中,已知連桿的感覺長度為l1和l2,并且已知兩個關節的轉動角度分別為θ1和θ2,那么其末端執行器的位置(x,y)可以根據三角函數求出。
x=l1cos(θ1)+l2cos(θ1+θ2)
y=l1sin(θ1)+l2sin(θ1+θ2)
就可以求出x,y的坐標了。
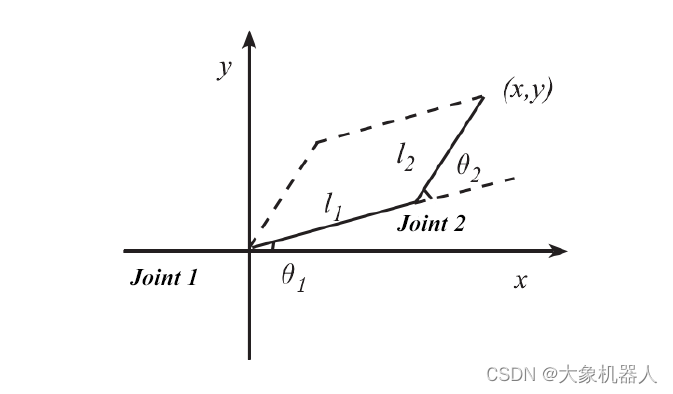
在實際應用中,我們通常會直接在三維空間中直接進行計算,我們可以使用齊次坐標來進行轉換,在齊次坐標中,一個二維點(x, y)可以表示為一個三維點(x, y, 1),一個三維點(x, y, z)可以表示為一個四維點(x, y, z, 1)。通過這種方式,我們可以使用相同的矩陣乘法操作來描述平移和旋轉。
例如,一個二維的平移變換可以表示為以下形式的3x3矩陣:
[[1, 0, dx], [0, 1, dy], [0, 0, 1]]
其中,dx和dy表示在x軸和y軸方向上的平移距離。同樣,一個二維的旋轉變換可以表示為以下形式的3x3矩陣:
[[cos(theta), -sin(theta), 0], [sin(theta), cos(theta), 0], [0, 0, 1]]
其中,theta表示旋轉角度,也就是DH參數中的θ。
通過將所有關節的變換矩陣相乘,我們就可以得到從機器人基座到末端執行器的總變換。這就是正運動學的基本計算過程。這個過程可以用以下的數學形式來表示:
T = A1 * A2 * A3 * ... * An
其中 T 是總變換矩陣,Ai 是第 i 個關節的變換矩陣,n 是關節的數量。注意,矩陣乘法不滿足交換律,所以乘法的順序很重要。最終得到的T總變化矩陣算出來的結果就是機械臂末端相對于基座的坐標。提前了解DH模型,對理解后面的矩陣變換很有幫助。
逆運動學
逆向運動學是指根據機械臂末端執行器的位置和姿態,計算機械臂各個關節的角度。剛好跟正運動學反過來,是求取各個關節的角度。逆運動學的計算通常要比正運動學復雜得多,這是一個從效果反推原因的過程,通常需要解決非線性方程組,而且解可能不唯一,或者根本不存在。我們還是舉例說明,以2自由度的平面機械臂來做一個了解。我們已知(x,y)的值,要求出θ1和θ2的角度。

首先我們可以x,y到原點的位置的距離d,這可以勾股定理得到(sqrt代表平方根)
d = sqrt(x^2 + y^2)
然后,我們可以使用余弦定理來求解第二個關節的角度θ2。余弦定理可以描述三個邊長已知的三角形中,任何一個角的余弦值。在這里,我們可以將d,L1和L2看作是三個邊長,然后求解θ2:
cos(theta2) = (L1^2 + L2^2 - d^2) / (2 * L1 * L2)
因為θ2可能有兩個解(順時針和逆時針),所以我們需要根據實際情況來選擇合適的解。
最后,我們可以使用正弦定理或余弦定理來求解第一個關節的角度θ1。正弦定理可以描述三個邊長和對應的角的正弦值之間的關系。在這里,我們可以將d,L1和θ1看作是三個已知的值,然后求解θ1:
theta1 = atan2(y, x) - atan2(L2 * sin(theta2), L1 + L2 * cos(theta2))
求解完之后就可以得知各個關節的角度了,這是在二維的空間中的求解方法,在三維空間中的計算方法也是一樣的道理,在計算的時候得考慮機械臂關節的限制,以及其他的因素來決定最終的角度。
7軸機械臂實例
接下會用到python對myArm進行編程,用到的是pymycobot庫。
正運動學關節控制
正運動學算法通常有一個確定的結果,正運動學的目標是根據給定的關節角度,計算機械臂執行器的位置和姿態,只存在唯一的結果。下面是使用角度控制的代碼:
from pymycobot import Myarm import time # create myarm object ma = Myarm('/dev/ttyAMA0',115200) ma.send_angles([degree_list],speed) # send_angles function def send_angles(self, degrees, speed): """Send the degrees of all joints to robot arm. Args: degrees: a list of degree values(List[float]).n for mycobot: [0.0, 0.0, 0.0, 0.0, 0.0, 0.0].n for mypalletizer: [0.0, 0.0, 0.0, 0.0] for mypalletizer 340: [0.0, 0.0, 0.0] for myArm: [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0].n speed : (int) 1 ~ 100 """ # self.calibration_parameters(degrees=degrees, speed=speed) degrees = [self._angle2int(degree) for degree in degrees] return self._mesg(ProtocolCode.SEND_ANGLES, degrees, speed)

這就是最直觀的正運動學算法的控制,關節角度控制機械臂運動。
逆運動學算法控制,坐標控制
前面也有提及到,你運動學算法相對來說復雜很多,可能存在多個解的情況,也可能存在無解的情況。逆運動學算法的控制是通過控制機械臂末端坐標的變化,讓機械臂前往下一個坐標位置。我們用python編寫控制坐標運動的代碼:
from pymycobot import Myarm import time # create myarm object ma = Myarm('/dev/ttyAMA0',115200) ma.send_coords([coordinates_list],speed,mode) # mode: 0:linear motion,1:nonlinear motion def send_coords(self, coords, speed, mode=None): """Send all coords to robot arm. Args: coords: a list of coords value(List[float]). for mycobot :[x(mm), y, z, rx(angle), ry, rz]n for mypalletizer: [x, y, z, θ] for mypalletizer 340: [x, y, z] speed : (int) 0 ~ 100 mode : (int) 0 - angluar, 1 - linear (mypalletizer 340 does not require this parameter) """ # self.calibration_parameters(coords=coords, speed=speed) coord_list = [] for idx in range(3): coord_list.append(self._coord2int(coords[idx])) for angle in coords[3:]: coord_list.append(self._angle2int(angle)) # print(coord_list) if mode is not None: return self._mesg(ProtocolCode.SEND_COORDS, coord_list, speed, mode) else: return self._mesg(ProtocolCode.SEND_COORDS, coord_list, speed)
7軸機械臂又被稱之為冗余機器人,多的一個軸通常用于提供更多的靈活性和運動自由度,所以就出現了這么一個現象,機械臂的末端坐標值保持不變的時候,會有許多不同的姿態。

這就是開頭說到的逆運動學的特點,同一個坐標下有許多不同的解。在坐標控制中還有一個關鍵的信息就是線性運動和非線性運動,主要是指機械臂末端的運動路徑的類型。
線性運動:在這種模式下,機器人末端執行器在兩個點之間直線移動。這就意味著,無論機器人的關節如何移動,末端執行器都會沿著直線路徑從一點移動到另一點。這種類型的運動通常在需要精確位置控制的應用中使用,例如在裝配線上的裝配任務。
非線性運動:在這種模式下,機器人末端執行器的路徑不是直線,而是一條曲線。這種類型的運動可以使機器人在復雜的環境中更靈活地移動,例如在需要避開障礙物或在特定的路徑上移動的情況下。
總結
在我們探討了正逆運動學的基本概念以及數學原理后,我們可以看到這兩個概念在機械臂中的控制是特別重要的。然而,正運動學和逆運動學只是機械臂控制的一部分。在實際應用中,我們還需要考慮到動力學、控制理論、傳感器反饋、以及實際硬件的限制。
隨著技術的發展,機械臂將在很多領域發揮越來越大的作用,包括制造業、醫療保健、家庭服務、搜索和救援等。通過深入理解這些知識,我們可以更加的了解什么是機械臂,讓它在各種應用中發揮更大的作用。
如果你喜歡這篇文章的話歡迎在下方留言或者點贊,你的支持是我們更新的動力!
審核編輯 黃宇
-
機器人
+關注
關注
211文章
28524瀏覽量
207553 -
開源
+關注
關注
3文章
3371瀏覽量
42580 -
python
+關注
關注
56文章
4800瀏覽量
84820 -
機械臂
+關注
關注
12文章
515瀏覽量
24634
發布評論請先 登錄
相關推薦
機械臂的高效運作,連接器起關鍵作用
【原創】 drawbot 平面機械臂scara寫字畫畫機器人DIY教程貼
開源六軸協作機器人myCobot 320結合人臉表情識別情緒!

機器視覺控制軸運動原理是什么
國產Cortex-A55人工智能教學實驗箱_基于Python機械臂跳舞實驗案例分享
大象機器人發布智能遙操作機械臂組合myArm M&C,加速具身智能研究與發展!

機械臂技術的前沿探索:年度案例回顧!
【國產FPGA+OMAPL138開發板體驗】(原創)2.手把手玩轉游戲機械臂
大象機器人六軸協作機械臂myCobot 320 進行手勢識別!
使用ChatGPT學習大象機器人六軸協作機械臂mechArm!

【正運動】高速高精,超高實時性的PCIe EtherCAT實時運動控制卡 | PCIE464
機器人運動學中的非完整約束與運動模型推導





 開源七軸myArm協作機械臂正逆運動學技術講解
開源七軸myArm協作機械臂正逆運動學技術講解











評論