概述

本篇文章從一維例子出發(fā)，介紹自適應(yīng)有限元中幾種常見(jiàn)的后驗(yàn)誤差，并且對(duì)比各自的優(yōu)勢(shì)。

后驗(yàn)誤差按照實(shí)現(xiàn)方式，可以分為：基于恢復(fù)梯度的后驗(yàn)誤差；基于殘差的后驗(yàn)誤差；基于物理場(chǎng)規(guī)律的后驗(yàn)誤差；以及試測(cè)的基于純粹梯度的后驗(yàn)誤差。下面就這幾種后驗(yàn)誤差給出常見(jiàn)的表達(dá)式與測(cè)試結(jié)果。

1.幾種后驗(yàn)誤差的基本原理

A.基于恢復(fù)梯度

這種后驗(yàn)誤差在之前介紹過(guò)，其基于理論：仿真數(shù)值解的精度在未知點(diǎn)位置的精度最高；數(shù)值解的梯度在高斯點(diǎn)位置精度最高；

因此可以通過(guò)獲取單元內(nèi)高斯點(diǎn)的高精度梯度解，進(jìn)而通過(guò)插值等方式獲得整個(gè)區(qū)域內(nèi)其他精度低位置的梯度值，對(duì)比即可獲得每個(gè)單元的梯度誤差。詳細(xì)可參考：

B.基于殘差的后驗(yàn)誤差

這種后驗(yàn)誤差基于微分方程，根據(jù)理論，有限元求解求解結(jié)果一定是滿(mǎn)足原微分方程的，因此將數(shù)值解帶入到微分方程中，等式兩邊理論上應(yīng)該成立。但是由于有限元本身求解的是弱解問(wèn)題，因此存在一定誤差，而這誤差則可以用來(lái)評(píng)價(jià)該點(diǎn)的精度，以此作為后驗(yàn)誤差。

一般的微分方程可以寫(xiě)成：

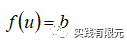
基于殘差的后驗(yàn)誤差表示為：

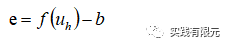
C.基于物理場(chǎng)規(guī)律的后驗(yàn)誤差

這種后驗(yàn)誤差基于本身研究問(wèn)題的物理規(guī)律，根據(jù)物理規(guī)律，指定每個(gè)單元上的誤差標(biāo)準(zhǔn)。

例如一維電磁場(chǎng)衰減，物理場(chǎng)滿(mǎn)足電場(chǎng)、磁場(chǎng)在節(jié)點(diǎn)上連續(xù)；有限元本身只保證了電場(chǎng)連續(xù)，因此可以通過(guò)求解節(jié)點(diǎn)兩側(cè)單元的磁場(chǎng)是否連續(xù)作為誤差判斷標(biāo)準(zhǔn)。

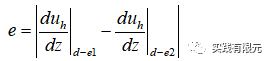
式子表示，使用內(nèi)部節(jié)點(diǎn)兩側(cè)單元求解該點(diǎn)的磁場(chǎng)，兩者的差值作為判斷單元計(jì)算精度的標(biāo)準(zhǔn)。其實(shí)不難發(fā)現(xiàn)，本例子描述的基于物理規(guī)律后驗(yàn)誤差本質(zhì)上是恢復(fù)梯度的后驗(yàn)誤差。在二維三維中則不是如此。

D.基于純粹梯度的后驗(yàn)誤差

這是作者梯度原理猜想的一種后驗(yàn)誤差，其原理是：對(duì)于只要求表面節(jié)點(diǎn)精度而言，求解該點(diǎn)對(duì)于每個(gè)單元的梯度，因此獲得每個(gè)單元對(duì)于該點(diǎn)的影響程度，對(duì)于影響大的網(wǎng)格進(jìn)行加密。

由于測(cè)試案例使用簡(jiǎn)單的一維模型，因此采用擾動(dòng)法求解梯度矩陣。

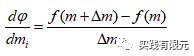
2.測(cè)試

本次測(cè)試案例以一維電磁場(chǎng)衰減為例，分別對(duì)上述幾種后驗(yàn)誤差進(jìn)行測(cè)試，其中A、C在本例中是一種后驗(yàn)誤差。測(cè)試標(biāo)準(zhǔn)以在研究區(qū)域發(fā)射電場(chǎng)表面的電阻率變化為標(biāo)準(zhǔn)。

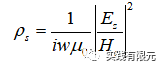
A.測(cè)試一維電場(chǎng)在均勻介質(zhì)中的傳播規(guī)律

初始網(wǎng)格與計(jì)算的電場(chǎng)如下，10個(gè)均勻網(wǎng)格單元，頻率10000Hz。該網(wǎng)格計(jì)算的視電阻率為138歐姆米，與理論值100相差甚遠(yuǎn)。

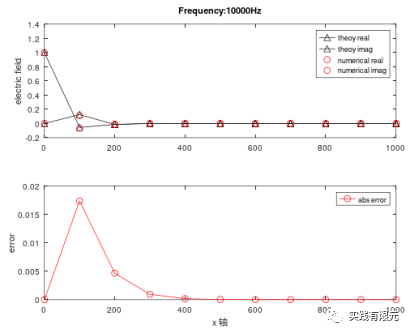
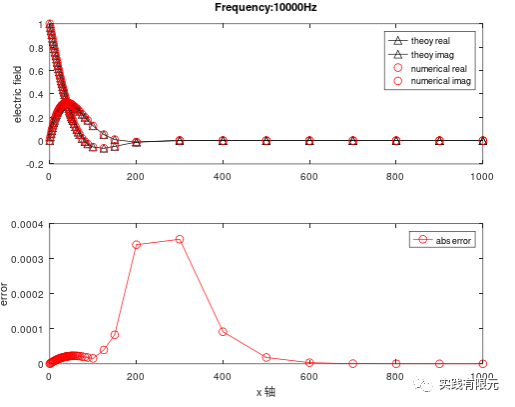
a.基于恢復(fù)梯度A、物理場(chǎng)C的后驗(yàn)誤差測(cè)試結(jié)果：

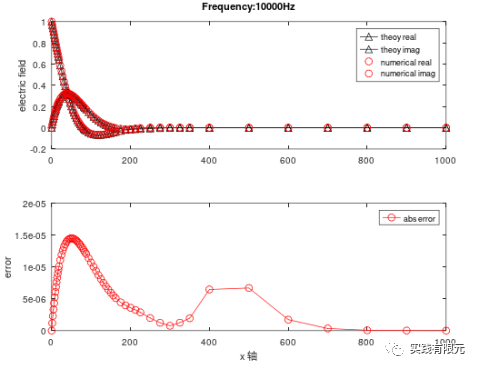
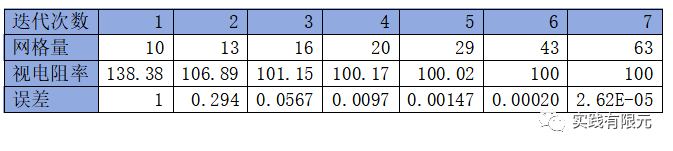
b.基于殘差B的后驗(yàn)誤差測(cè)試結(jié)果：

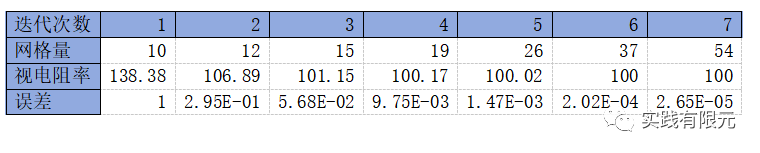
c.基于純粹梯度D的后驗(yàn)誤差測(cè)試結(jié)果：

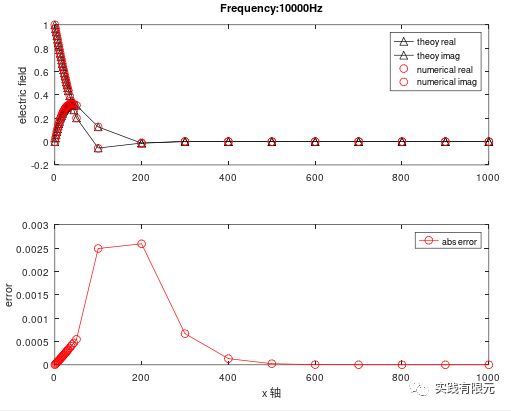
不難看出，三種后驗(yàn)誤差加密得到的網(wǎng)格差異明顯。

從電場(chǎng)本身的精度來(lái)看，基于恢復(fù)梯度的A、C后驗(yàn)誤差的精度最大，而純粹基于梯度D的后驗(yàn)誤差精度最低。

從加密程度看，基于純粹梯度D的加密集中在0點(diǎn)附近；而基于恢復(fù)梯度A、C則相對(duì)分散開(kāi)；

從視電阻率精度結(jié)果來(lái)，三者誤差均達(dá)到了可控范圍0.01%內(nèi)，但是基于恢復(fù)梯度A、C的網(wǎng)格量大于基于殘差B大于純粹梯度D。

因此，如果考慮視電阻率精度與網(wǎng)格量角度來(lái)看，基于純粹梯度的方式D是最佳的。其次是基于殘差，最后才是基于恢復(fù)梯度。

B.測(cè)試一維電場(chǎng)在非均勻介質(zhì)中的傳播規(guī)律

一維材料參數(shù)模型如下，在研究區(qū)域內(nèi)存在低阻1歐姆米的區(qū)域。

a.基于恢復(fù)梯度A、物理場(chǎng)C的后驗(yàn)誤差測(cè)試結(jié)果：

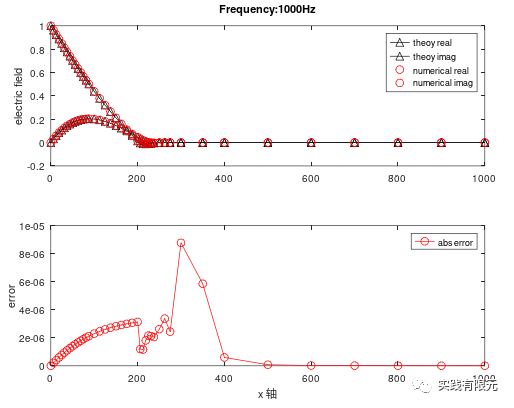
b.基于殘差B的后驗(yàn)誤差測(cè)試結(jié)果：

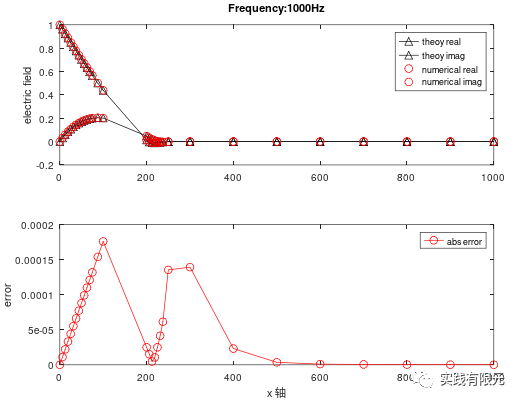
c.基于純粹梯度D的后驗(yàn)誤差測(cè)試結(jié)果：

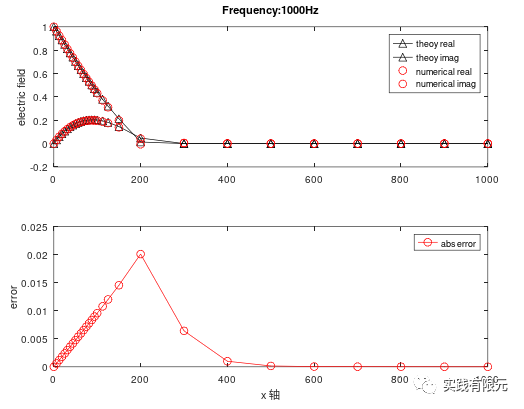
三種后驗(yàn)誤差的視電阻率在該頻率下的計(jì)算結(jié)果：

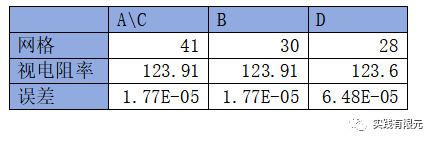
上述測(cè)試的視電阻率理論結(jié)果為123.91，可見(jiàn)整體上看基于殘差的后驗(yàn)誤差的精度和網(wǎng)格量是最佳的。純粹基于梯度D的結(jié)果精度要稍微低一些。繼續(xù)測(cè)試了幾組頻率，對(duì)比結(jié)果：

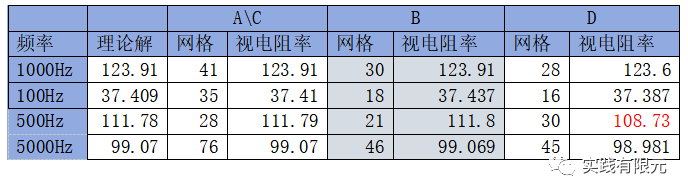
整體來(lái)說(shuō)，基于殘差B的后驗(yàn)誤差方式的效果是最佳的，網(wǎng)格量少，視電阻率也幾乎和理論解一致；基于恢復(fù)梯度的A、C精度是最高的，但是網(wǎng)格量也是最大的；基于純粹梯度的D在頻率500Hz的時(shí)候誤差太大。

3.總結(jié)

使用一維模型，初步測(cè)試了幾種后驗(yàn)誤差的自適應(yīng)收斂效果，其中整體上最佳方案是基于殘差的后驗(yàn)誤差，其次是基于恢復(fù)梯度、基于物理磁場(chǎng)；基于純粹梯度的后驗(yàn)誤差雖然網(wǎng)格量有時(shí)候很少，但是可能會(huì)計(jì)算不準(zhǔn)確。