1.graph embedding（GE）

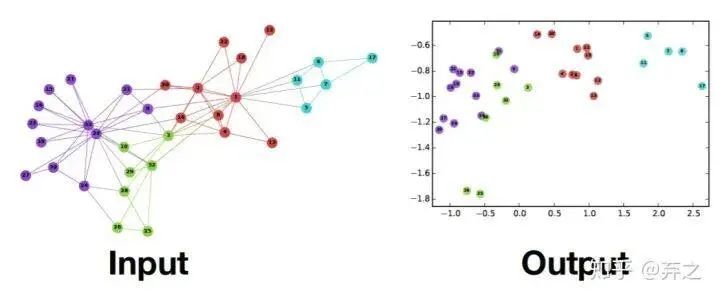
GE做的事情是將圖表示成為低維向量，類似與nlp將詞、句子等embedding。distributed representation的一體化過程，萬物皆可embedding。

• 將圖中的節(jié)點表示成低維、實值、稠密的向量形式，使得得到的向量形式可以在向量空間中具有表示以及推理的能力，這樣的向量可以用于下游的具體任務(wù)中。例如用戶社交網(wǎng)絡(luò)得到節(jié)點表示就是每個用戶的表示向量，再用于節(jié)點分類等；
• 將整個圖表示成低維、實值、稠密的向量形式，用來對整個圖結(jié)構(gòu)進行分類；

在圖中最重要的兩個部分就是

• encoder：map到低維向量
• similarity function：如何度量相似度（什么樣的node的embedding應(yīng)該相似？）

www-18有個很好的tutorial：Representation Learning on Networks[1]，可以參考

1.1.圖中學(xué)習(xí)的分類

• 歸納學(xué)習(xí)（Inductive Learning）：先從訓(xùn)練樣本中學(xué)習(xí)到一定的模式，然后利用其對測試樣本進行預(yù)測（即首先從特殊到一般，然后再從一般到特殊），這類模型如常見的貝葉斯模型。在GAT中
• 轉(zhuǎn)導(dǎo)學(xué)習(xí)（Transductive Learning）：先觀察特定的訓(xùn)練樣本，然后對特定的測試樣本做出預(yù)測（從特殊到特殊），這類模型如k近鄰、SVM等。在GAT中采用的是在Cora 數(shù)據(jù)集上優(yōu)化網(wǎng)絡(luò)結(jié)構(gòu)的超參數(shù)，應(yīng)用到Citeseer 數(shù)據(jù)集

1.2.相似度度量方法

度量方式可以進行如下分類

• Adjacency-based Similarity：相鄰節(jié)點相似，能表征這兩個是否有連接

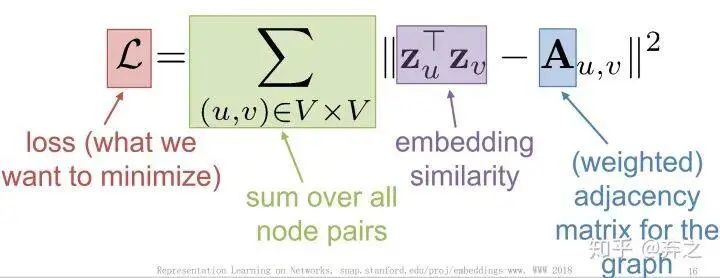
• Multi-hop Similarity：考慮k跳的neighbor

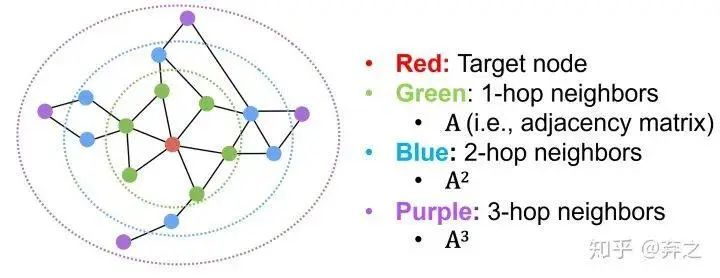
典型代表就是GraRep（Cao et al, 2015）和HOPE (Yan et al., 2016)了，一個考慮不同跳數(shù)分別訓(xùn)練然后concatenate，一個考慮neighbor的重復(fù)程度。

• Random Walk Approaches：典型代表是deepwalk和node2vec，采用和nlp的相似方法，共現(xiàn)頻率來度量。
• GNN階段：neighborhood aggregation

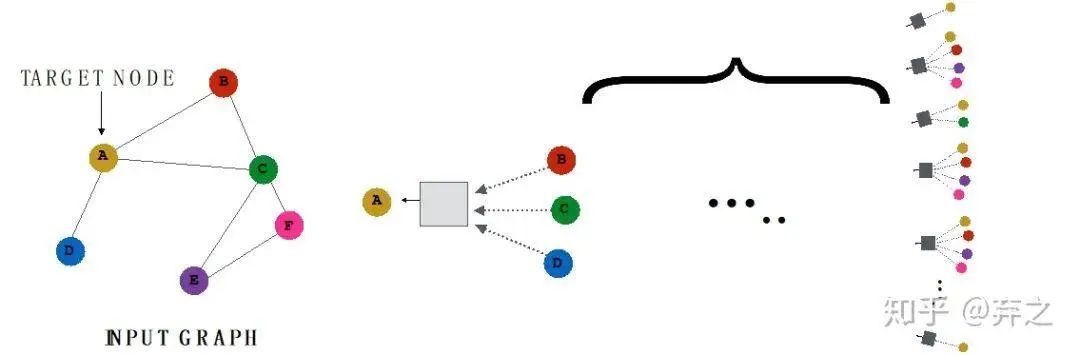
neighborhood aggregate的方法可以對每個target node來刻畫以它為中心的計算圖，如

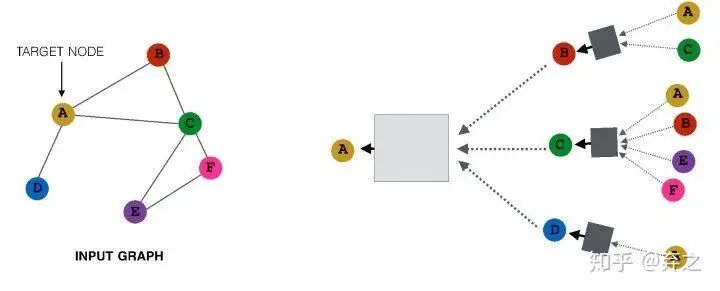
對于每一個node，都構(gòu)成了一個計算圖，而且每個node的計算圖都有差別

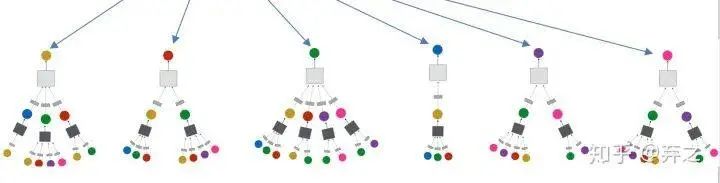
我們可以看到GNN逐漸成形了，考慮簡單的aggregate方式可以表示成這個樣子

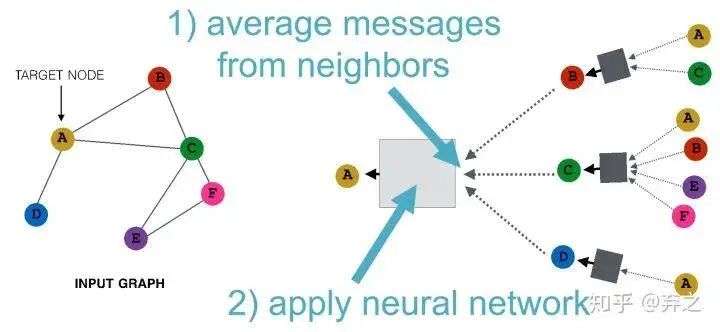
數(shù)學(xué)表示也十分清晰了，如下圖， 就是節(jié)點 的第 個時間步（或第 layer）的embedding

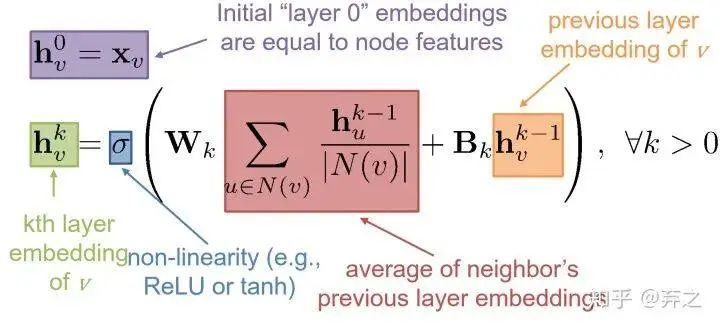
這就好家伙了，上圖中一些參數(shù)就可以generalize到一些unseen的點了，如下圖

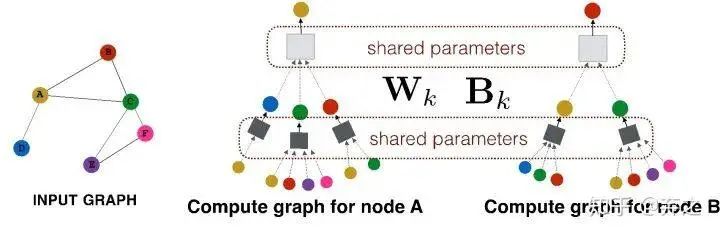
這種能力稱之為inductive capability

早期邁向neural的過程借鑒了nlp的方法，如deepwalk[2]利用word2vec的方法，因為語料中詞語出現(xiàn)的次數(shù)與在圖上隨機游走節(jié)點被訪問到底的次數(shù)都服從冪律分布，采用隨機游走進行采樣出序列，然后按照word2vec的方法進行訓(xùn)練。

word2vec出現(xiàn)在2013年，deepwalk 14年就出現(xiàn)了，緊隨其后。

后來來也出現(xiàn)了很多，如Line，node2vec，struc2vec，聽名字就知道，Line和node2vec是在描述圖像時刻畫節(jié)點的embedding，不過在游走的方式上進行探索，是DFS還是BFS還是both呢？到了struc2vec開始走節(jié)點空間結(jié)構(gòu)的相似性這條路了。

其實這些已經(jīng)跨入到neural的階段了，但是還用的比較初級，沒有專門為graph設(shè)計的neural的模型，探索階段。

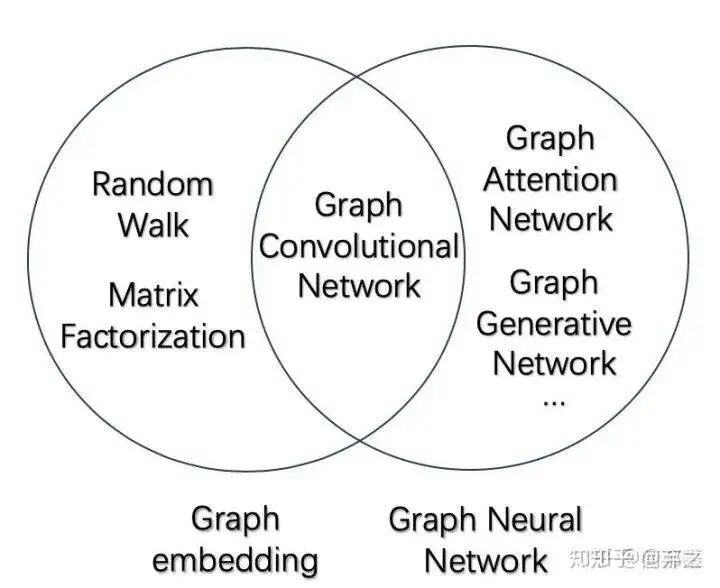
2.Graph neural network

2.1.Graph convolutional network(GCN)[3][4]

2.1.1.引子：熱傳播模型

圖卷積是基于熱傳播模型，即兩個點之間熱傳播的速度和兩點之間溫度差值成正比，把這個熱傳播模型推廣到圖上就是信息傳播的速度關(guān)系[5]。

假設(shè)它當(dāng)前的溫度為，在一個鏈條上的熱量傳播那么就有：

和單元的比熱容、質(zhì)量有關(guān)是個常數(shù)。右邊第一項是下一個單元向本單元的熱量流入導(dǎo)致溫度升高，第二項是本單元向上一個單元的熱量流出導(dǎo)致溫度降低。這是一個二階差分，即二階導(dǎo)數(shù)。

而且是相同算子的二階導(dǎo)，在高緯空間中是所有非混合二階偏導(dǎo)數(shù)之和，稱為拉普拉斯算子。

其中 這個符號代表的是對各個坐標(biāo)二階導(dǎo)數(shù)的加和，現(xiàn)在的主流寫法也可以寫作 。

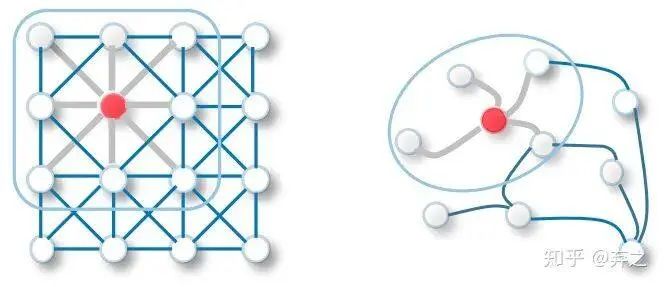
在離散圖模型中是相似的，和鏈條熱傳播不同的是沒有了上一個和下一個單元，有的是該節(jié)點所有的鄰接節(jié)點（鄰接矩陣刻畫），所以同樣的方式刻畫為

其中 是這個圖的鄰接矩陣，即所有相鄰節(jié)點的流入流出關(guān)系加和構(gòu)成了 這個節(jié)點溫度總的變化。

我們不妨用乘法分配律稍微對上式做一個推導(dǎo)：

即可以寫成這樣：

然后我們定義向量，那么就有：

其中被稱為度矩陣，只有對角線上有值，且這個值表示對應(yīng)的頂點度的大小。整理整理，我們得到：

回顧剛才在連續(xù)歐氏空間的那個微分方程：

二者具有一樣的形式。這實際上是同一種變換在不同空間上的體現(xiàn)。 就是其中最簡單常用的圖上的拉普拉斯算子矩陣。

GCN的neighborhood aggregation

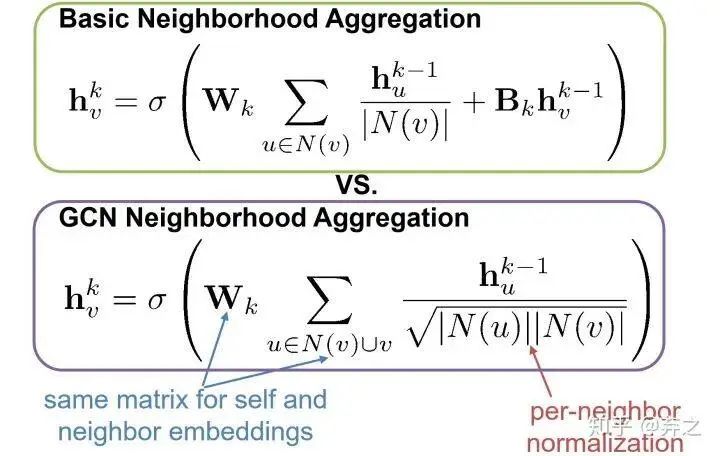
因為是熱傳播模型，流動的feature要流入每一個鄰接節(jié)點，所以加入了一個normalization，即節(jié)點的feature需要對所有neighbor取均值之后再進行流動。

2.1.2.熱傳播在graph上的求解：傅里葉變換

假設(shè)在圖中各個結(jié)點流動的東西不是熱量，而是特征（Feature），而是消息（Message），那么問題自然而然就被推廣到了GCN。所以GCN的實質(zhì)是什么，是在一張Graph Network中特征（Feature）和消息（Message）中的流動和傳播。

由于很多東西在頻域上會更好解決，而且拉普拉斯矩陣與傅里葉不謀而合，所以頻域上解決的方案來做。先來推導(dǎo)下傅里葉變換和拉普拉斯算子的關(guān)系

關(guān)于傅里葉變換的理解，可參照我之前的博客[6]。所以，傅里葉變換就被推廣為時域信號與特定空間上拉普拉斯算子特征函數(shù)的積分。

理解下這個公式，實對稱矩陣的特征空間的所有基能夠張出整個線性空間且它們兩兩正交，所以無論是拉普拉斯算子 還是拉普拉斯矩陣 ，它們的特征空間是一個滿秩且基兩兩正交的空間，所以把歐氏空間的 推廣到圖空間的 的這一組特征向量。正是同一個關(guān)系（Message Passing），同一種變換，在不同空間下的體現(xiàn)。

現(xiàn)在我們已經(jīng)得到了graph空間上的拉普拉斯算子 ，只需要對 求出其特征向量貌似就可以傅里葉變換了。等等，我們到底需要傅里葉變換干嘛？經(jīng)過前面的鋪墊，傅里葉變換做了一個空間的變換，而這個空間里的卷積就非常絕-卷積定理卷積和乘積的變換。

在傳統(tǒng)的譜圖卷積下，由卷積定理：

函數(shù)卷積的傅里葉變換是函數(shù)傅里葉變換的乘積。具體分為時域卷積定理和頻域卷積定理，時域卷積定理即時域內(nèi)的卷積對應(yīng)頻域內(nèi)的乘積；頻域卷積定理即頻域內(nèi)的卷積對應(yīng)時域內(nèi)的乘積，兩者具有對偶關(guān)系。

時域卷積（時域內(nèi)的卷積對應(yīng)頻域內(nèi)的乘積）如下：

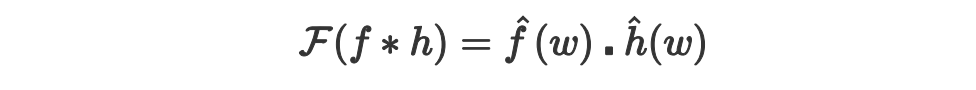
為了更好理解，證明方法如下：

因此，卷積的傅里葉等于傅里葉的積。

做逆變換

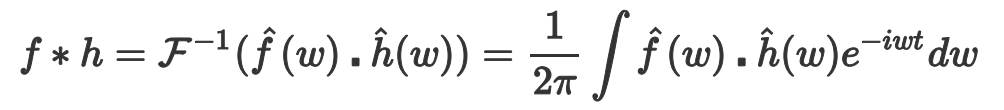
所以現(xiàn)在傅里葉域做乘積，然后做傅里葉逆變換，等價于在原空間直接做卷積。

2.2.分析下graph neural中哪些東西可以做？

如以上分析，本質(zhì)是圖上特征流動進行建模，然后利用傅里葉變換作為解決方案。

建模的方法還可以更加豐富，不一定流動速度非要和溫度查成正比，可以用更加復(fù)雜的模型，如神經(jīng)網(wǎng)絡(luò)等來進行更加復(fù)雜的建模。

建模時也可以不是單純對相鄰節(jié)點的影響進行簡單的加和，在實際建模中，我們的Aggregate不一定是加和，可以把Aggregate推廣成各種操作例如Sum Pooling，例如LSTM，例如Attention

解決方案也是如此，不一定非要在傅里葉域做，傅里葉做的譜圖卷積，現(xiàn)在也可以直接在原空間域做卷積-Spatial Convolution，如DCNN[7]，GAT[8]等

2.3.損失函數(shù)

對于無監(jiān)督的訓(xùn)練，其實就和nlp的預(yù)訓(xùn)練類似，訓(xùn)練出embedding，訓(xùn)練好之后再接下游任務(wù)。

對于有監(jiān)督的訓(xùn)練來說，如節(jié)點分類，一個比較簡單的方案就是對每個node的embedding接一個全連接層，就得到了一個損失函數(shù)

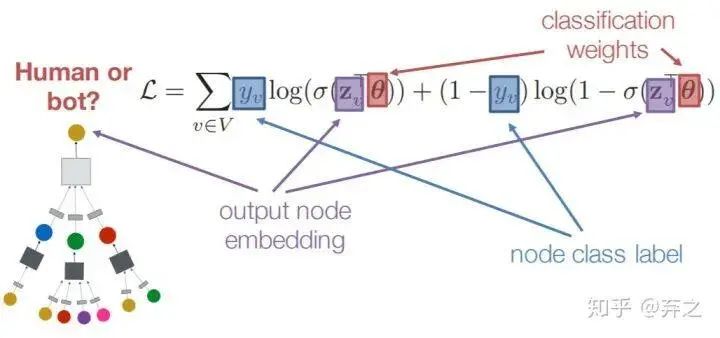
就是全連接層的權(quán)重。

3.GraphSAGE[9]：generalized aggregation方法

GCN是譜圖方法的代表，那么GraphSAGE就是非譜圖方法的代表。

如何進行更好的aggregate呢？

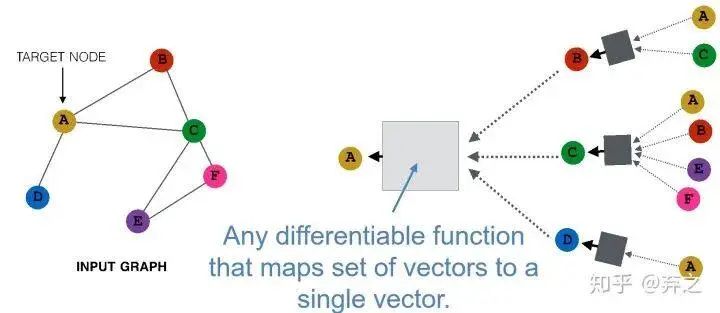
最后的這個黑盒里面可以裝的東西就多了，只要能把多個vector最后map到一個最終的vector就行

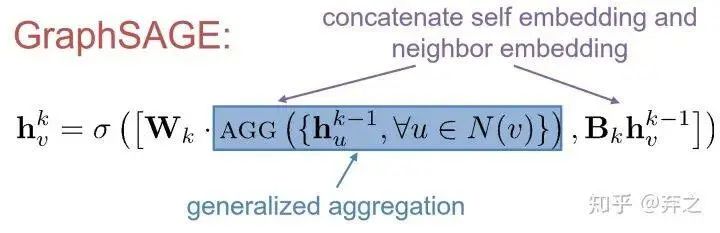
GraphSAGE則是將aggregate后的neighbor和本身的self-embedding這兩個concatenate到一起作為新的embedding，而不是傳統(tǒng)的把所有的embedding 加權(quán)求和，在原始論文中，作者提出這是一種很好的'skip connection'的方法。當(dāng)然AGG也可以有很多變體，不一定非要是aggregate，也可以是pool，lstm等等。

4.Gated Graph Neural Networks[10]：go deeper with RNN

GCNs and GraphSAGE generally only 2-3 layers deep，因此對于每個node所構(gòu)成的aggregate圖比較淺，如何走得更深呢？

可能會存在overfit或者梯度消失/爆炸，所以我們希望一個簡化可重用的模型，RNN！

每一層都使用相同的RNN單元，因為每個node 的neighbor的數(shù)量不同，所以先對所有neighbor做aggregate，我們稱之為“message”

就是節(jié)點v在step k的message

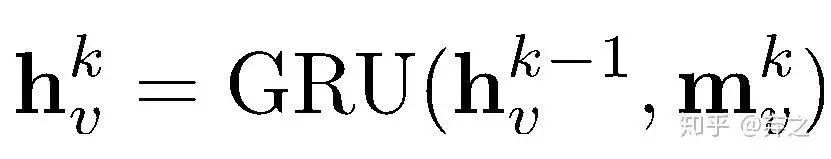
然后利用GRU對message和上一步狀態(tài)做處理得到新的狀態(tài)。

5.Graph level的embedding

直接把圖中所有node的embedding相加[11]

引入一個virtual node來代表graph，并用神經(jīng)網(wǎng)絡(luò)進行訓(xùn)練[12]

6.Graph attention network

利用attention在graph中動態(tài)確定和neighbor的權(quán)重，并利用mask只考慮鄰近的neighbor。

這篇文章用的attention與transfomer并不相同，只有一個突然formation matrix，而不是像attention中有q,k,v三個transformation

利用一個單層的全連接網(wǎng)絡(luò)來確定系數(shù)，將這兩個vector contatenate在一起輸入。然后進行softmax歸一化

即

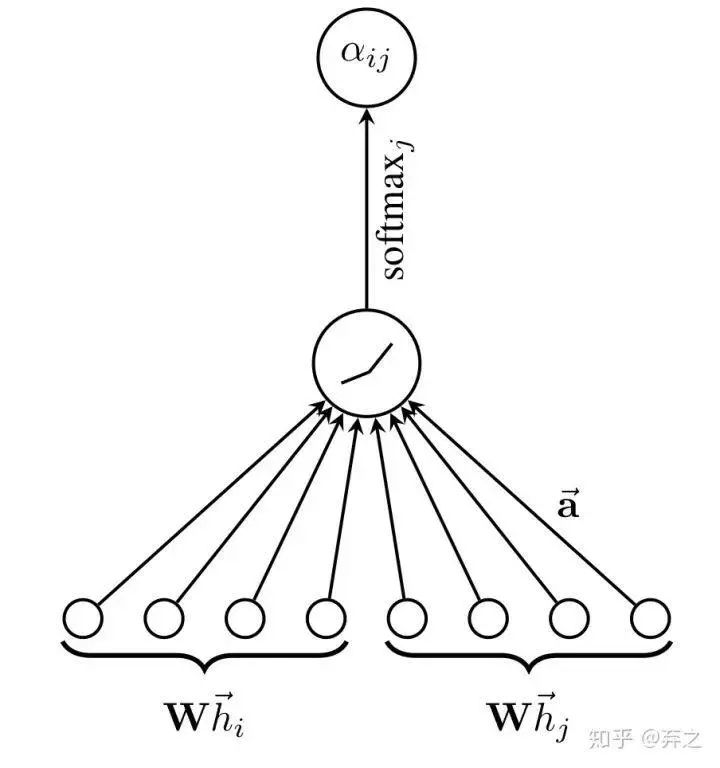
同時還采用了multi-head attention的機制

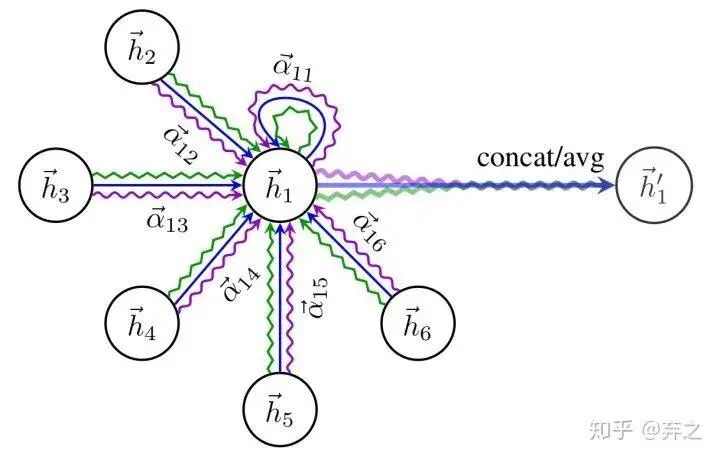
得到歸一化的注意力系數(shù)后，使用歸一化的值計算對應(yīng)特征的線性組合，作為每個頂點最后的輸出特征（最后可以加一個非線性層，σ）：

就是GAT輸出的節(jié)點i融合了鄰域信息的新特征

優(yōu)點（摘自原文）

• 計算高效：self-attention層的操作可以在所有的邊上并行(所有邊上算出的注意力系數(shù)可以共享），輸出特征的計算可以在所有頂點上并行。沒有耗時的特征值分解。單個的GAT計算F ′個特征的時間復(fù)雜度可以壓縮至 （前面是算所有node的 的復(fù)雜度，后面是算所有邊注意力系數(shù)的），F(xiàn)是輸入的特征數(shù)，|V|和|E|是圖中頂點數(shù)和邊數(shù)。復(fù)雜度與Kipf & Welling, 2017的GCN差不多。multi-head 中單個head的計算完全獨立且可以并行化。
• 魯棒性更強：和GCN不同，本文的模型可以對同一個 neighborhood的node分配不同的重要性，使得模型的capacity大增。
• 注意力機制以一種共享的策略應(yīng)用在圖的所有的邊上， 也是一種局部模型。在使用 GAT 時，無需訪問整個圖，而只需要訪問所關(guān)注節(jié)點的鄰節(jié)點即可，解決了之前提出的基于譜的方法的問題。因此這個方法有幾個影響：
• 圖不需要是無向的，可以處理有向圖（若 不存在，僅需忽略 即可）
• 可以直接應(yīng)用到 inductive learning：包括在訓(xùn)練過程中在完全未見過的圖上評估模型的任務(wù)上。
• GraphSAGE為每一個node都抽取一個固定尺寸的neighborhood，在計算的時候就不是所有的neighbor都能參與其中（不是所有都直接相連的neighbor都參與了aggregate嗎？）。此外，Hamilton的這個模型在使用基于LSTM的方法的時候假設(shè)了每個node的neighborhood的node一直存在著一個順序(RNN有輸入順序)。但是本文提出的方法就沒有這個問題，每次都可以將neighborhood所有的node都考慮進來，而且不需要事先假定一neighborhood的順序。

7.application example

如node classification和link prediction

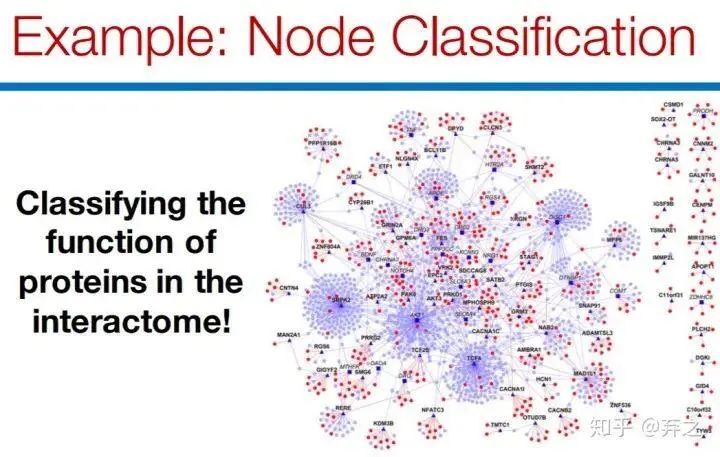
在實際的運用中，可以運用在

• recommendation
• Computational biology
• Practical insights

8.彩蛋：卷積的含義

卷積又稱褶積，來源于數(shù)字信號的處理

卷積的形式可以分兩類：

連續(xù)形式：

離散形式：

先對g函數(shù)進行翻轉(zhuǎn)，然后再把g函數(shù)平移到n，然后滑動疊加，這就是卷積的過程。

我們可以考慮在原始的數(shù)字信號處理中，對于一個輸入信號 ，我們想要得到一個在特定時間下的輸出信號， 可以看成信號的衰減過程（單位沖擊響應(yīng)函數(shù)）， 可以看成是想要得到輸出信號的時間。

比如以一天24h為例，我們希望得到一天結(jié)束時總的信號。在0時產(chǎn)生的信號 ，那么在24小時后衰減 ，在1時產(chǎn)生的信號為 ，那么這一天結(jié)束時衰減 ，以此類推，把每個時刻產(chǎn)生的信號以及到一天結(jié)尾時衰減程度相乘相加，就是所謂的卷積了，得到這一天結(jié)束時總的信號了。

那么對于圖片呢？

其實仍然是矩陣對應(yīng)元素的相乘相加，只是矩陣 可以看成filter是翻轉(zhuǎn)了。

但是其實CNN中用的更確切應(yīng)該稱為互關(guān)（co-relation），因為filter是沒有進行翻轉(zhuǎn)的，可以對比一下這兩者表達式的區(qū)別

co-relation:

convlution:

但是其實在CNN中不必那么嚴(yán)格的進行區(qū)分，學(xué)習(xí)一個翻轉(zhuǎn)前和翻轉(zhuǎn)后的filter并無不同，但是在數(shù)字信號處理中是不同的。

卷積擁有更多美好的性質(zhì)，如交換律結(jié)合律等，在CNN中互關(guān)基本也都被稱為卷積了。而且當(dāng)核對稱的時候，其實就完全一樣了。