本文轉載自公眾號:電子萬花筒

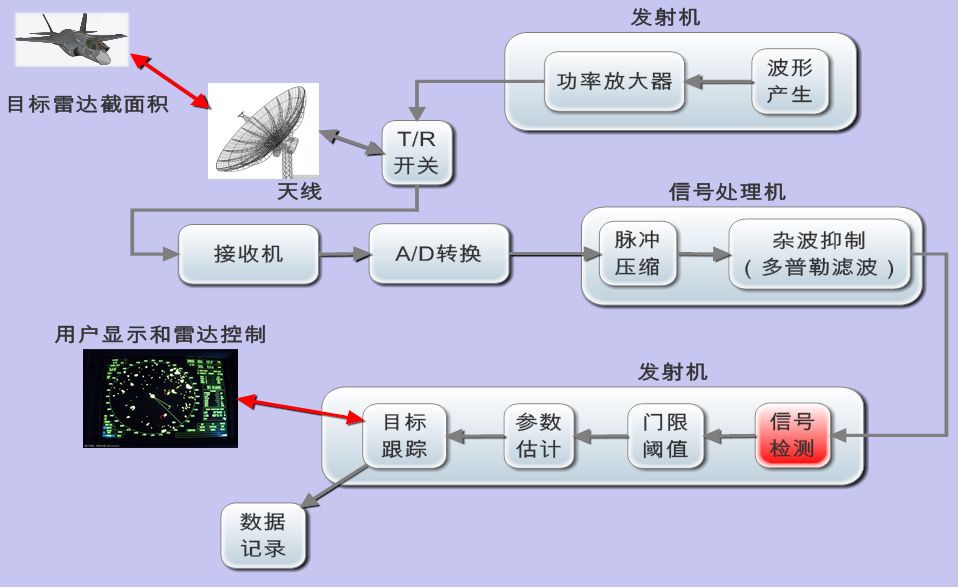
雷達回波信號有兩個狀態:有目標和沒有目標。雷達接收的回波中,既可能有目標回波也存在噪聲和雜波等各種干擾信號。所以雷達目標回波信號的檢測是在噪聲和雜波干擾背景中的二元信號最佳檢測問題。
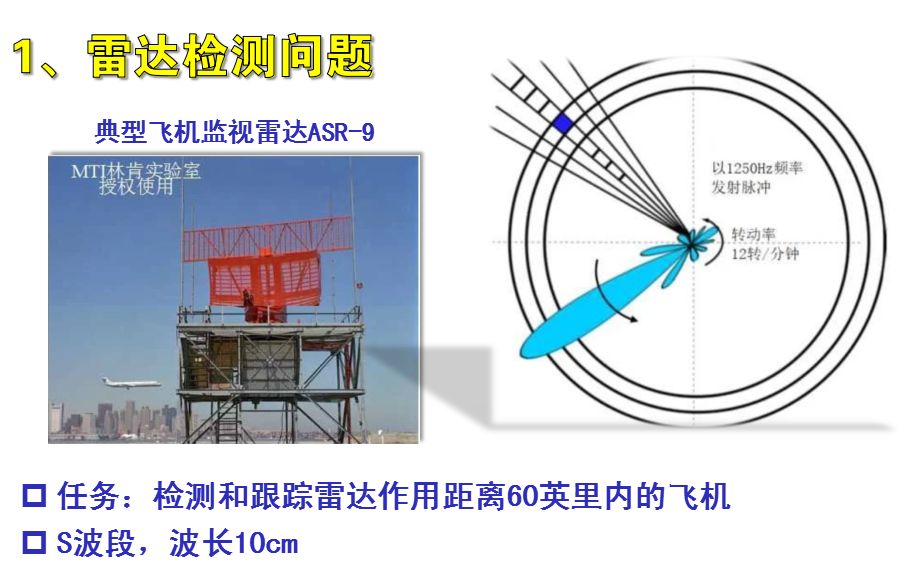
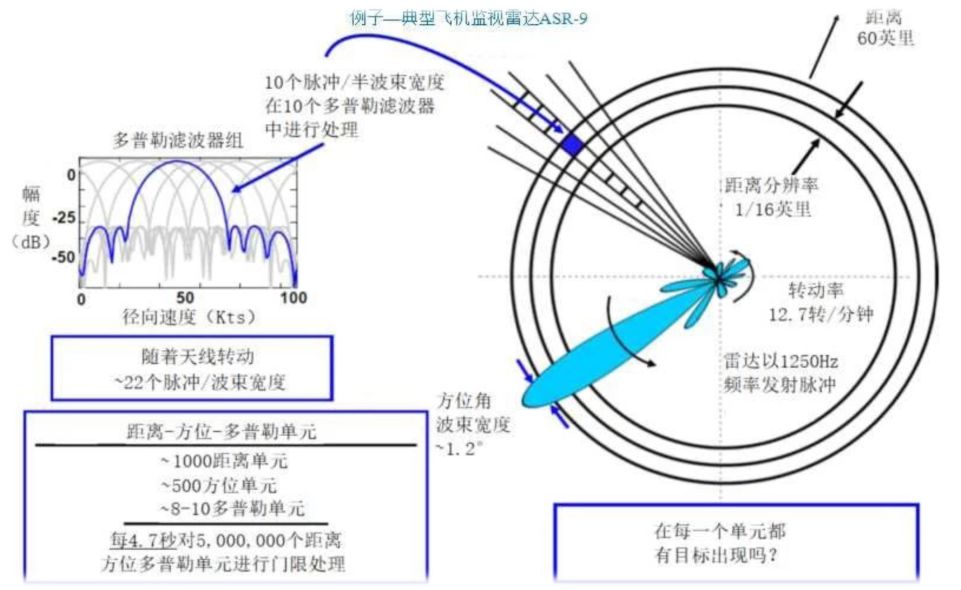
距離-方位-多普勒單元門限 雷達在掃描的過程中,在其距離單元-方位-多普勒單元上進行每個單元的目標檢測,以確定每個單元是否有目標出現。

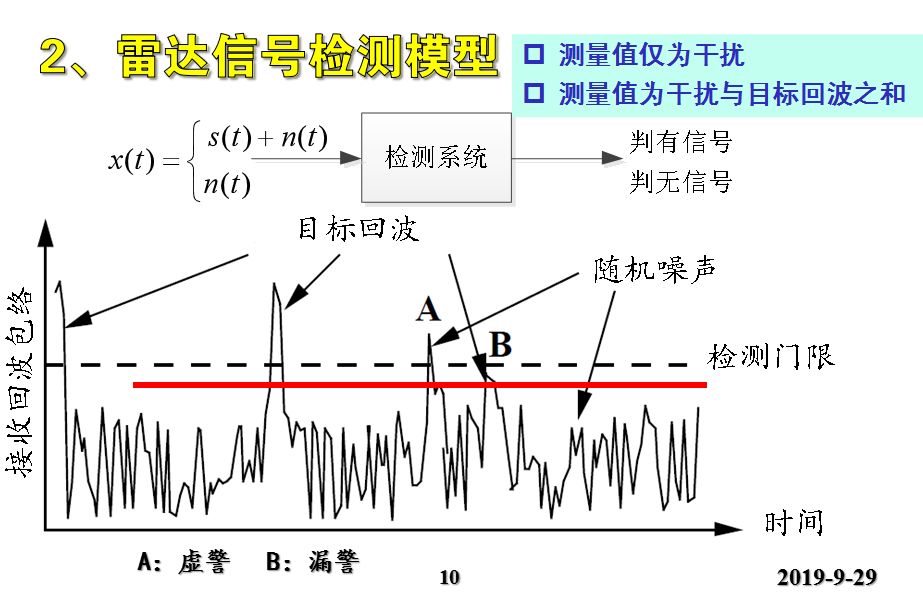

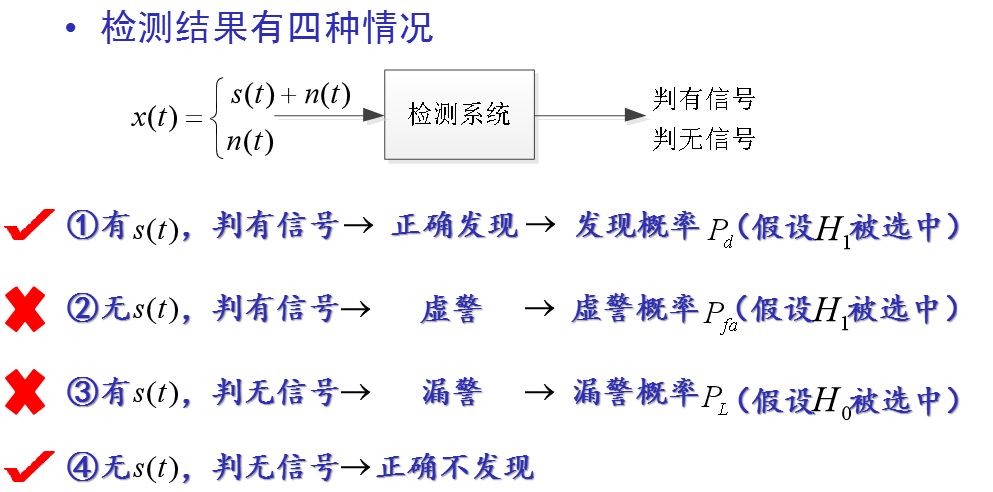
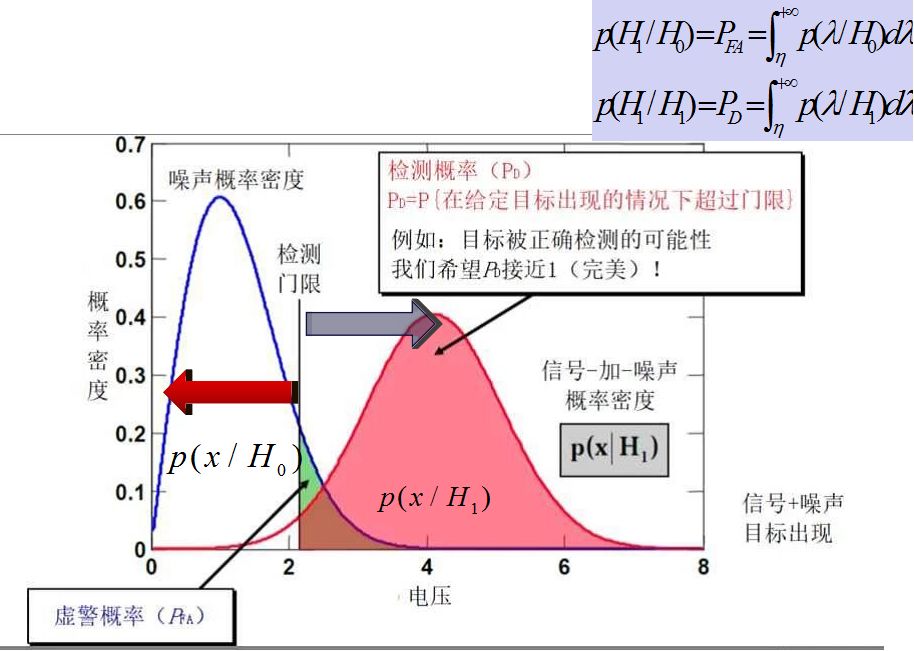
有信號-判為有信號-判決概率記為:P(H1/H1)
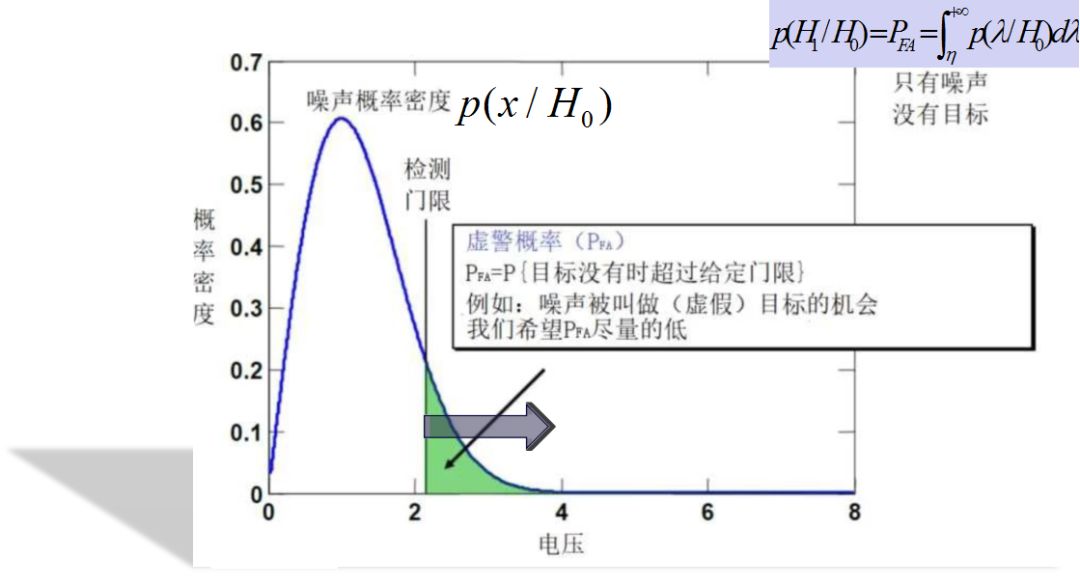
沒有信號-判為有信號-判決概率記為:P(H1/H0)
有信號-判為無信號-判決概率記為:P(H0/H1)
無信號-判為無信號-判決概率記為:P(H0/H0)
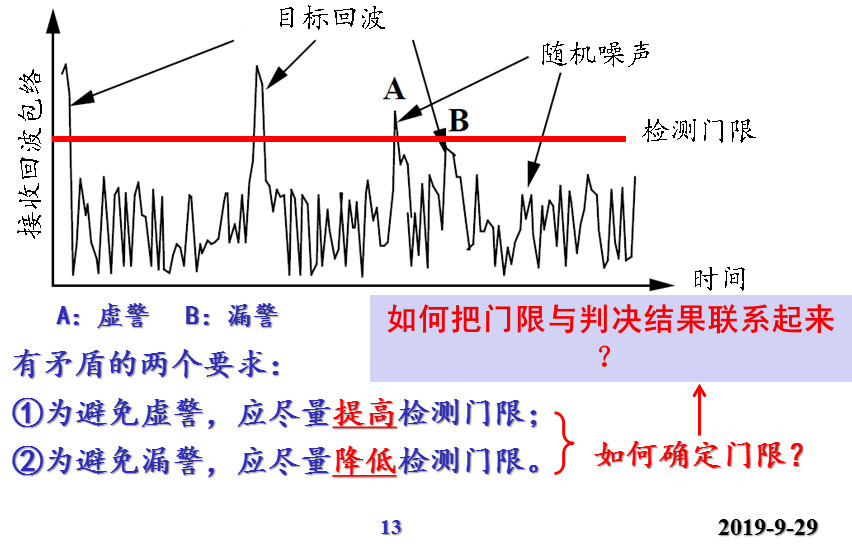
接收到的背景噪聲隨機起伏,
目標回波也是起伏的-隨機變量
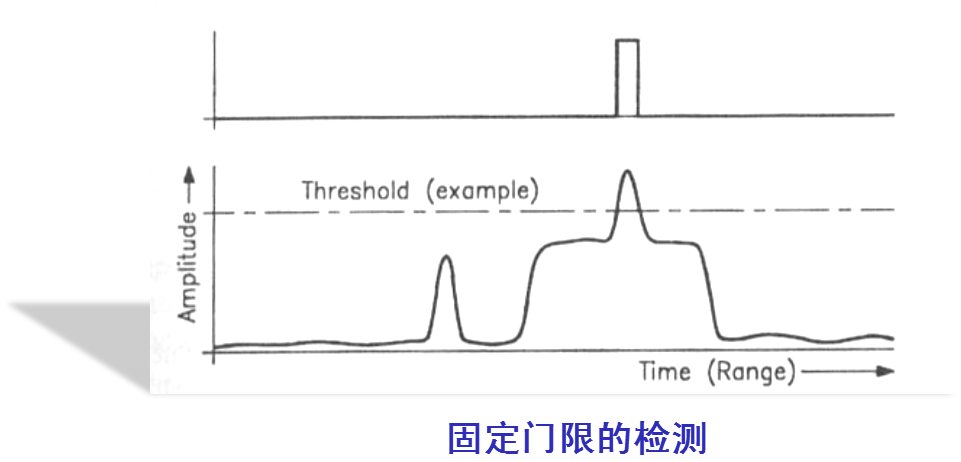
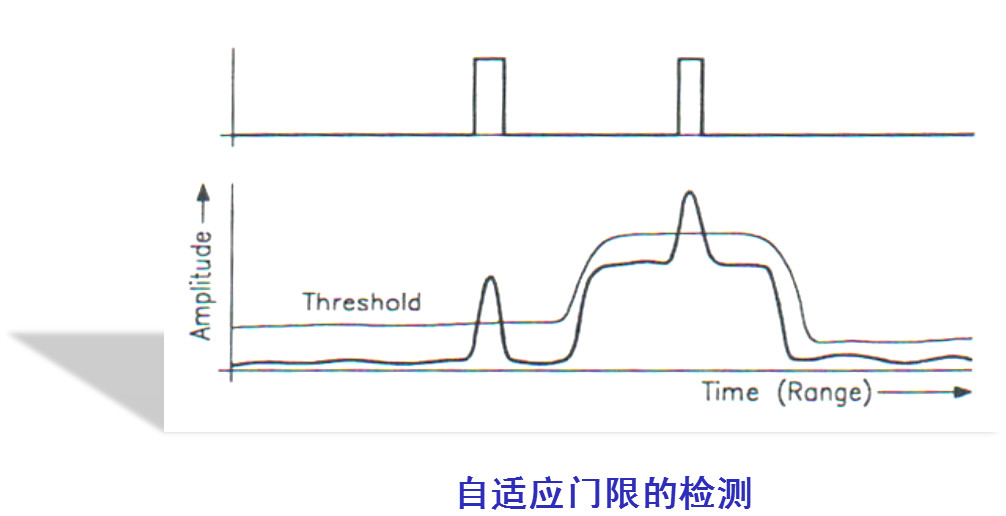
載給定距離上判決是否有目標出現,需要設置一個門限(常數或者變量)
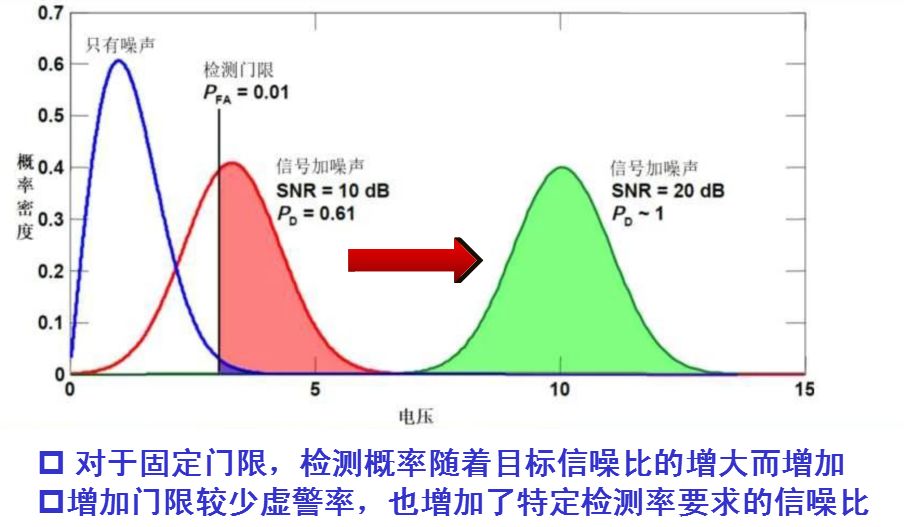
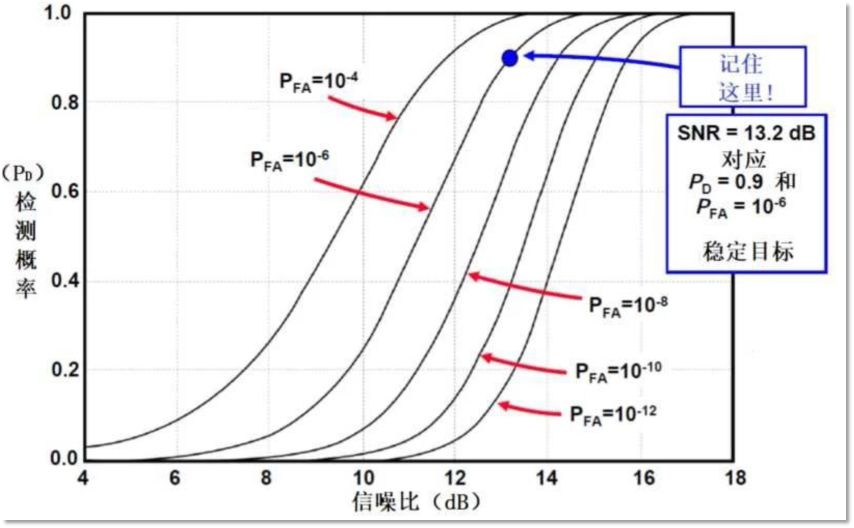
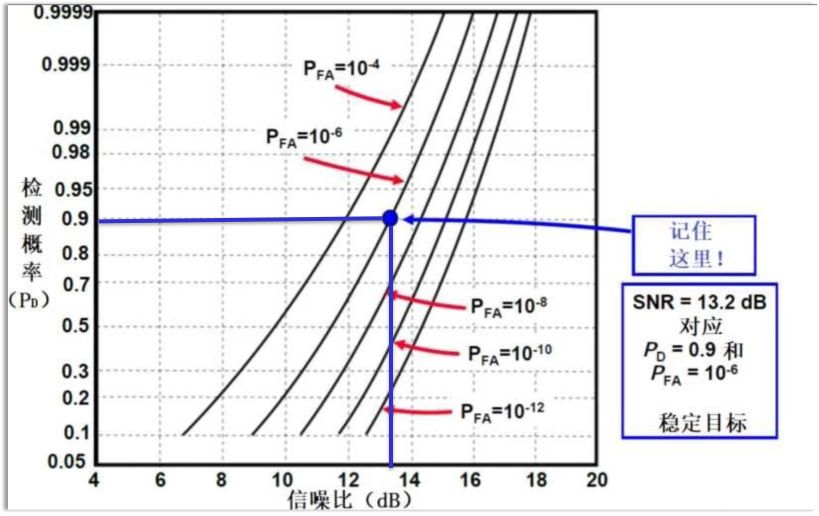
檢測性能(檢測概率)取決于目標對噪聲的強度和門限的設置
信號檢測要解決的主要問題就是通過合理設置門限,實現低虛警、低漏警和高發現概率。-門限確定=判決結果
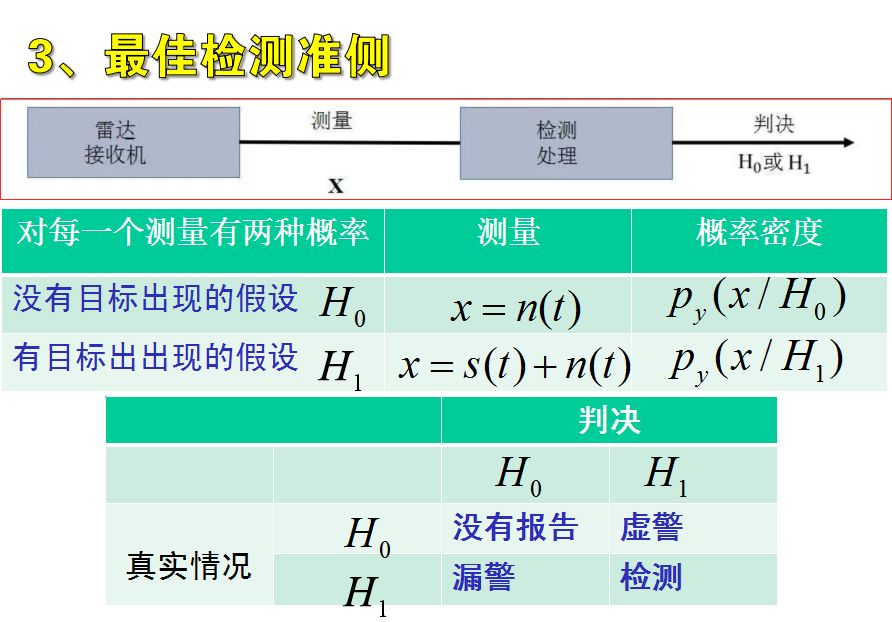
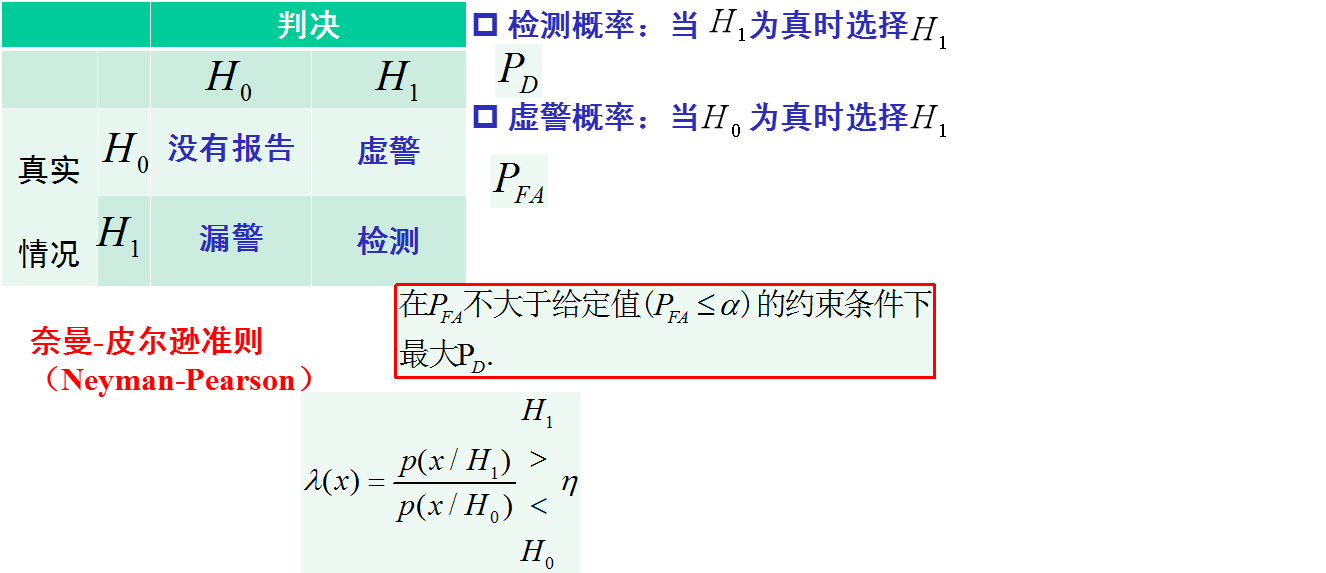
檢測的下一步是要決定使用哪種準則以便從兩種假設中挑選最有假設,在雷達領域通常使用貝葉斯準則的特殊情況,該準則被稱為奈曼-皮爾遜準側。
似然比函數-門限釋然比檢測門限

如果似然比函數在假設H0和H1下的概率密度函數分為:
Pfa=alfa 求檢測門限

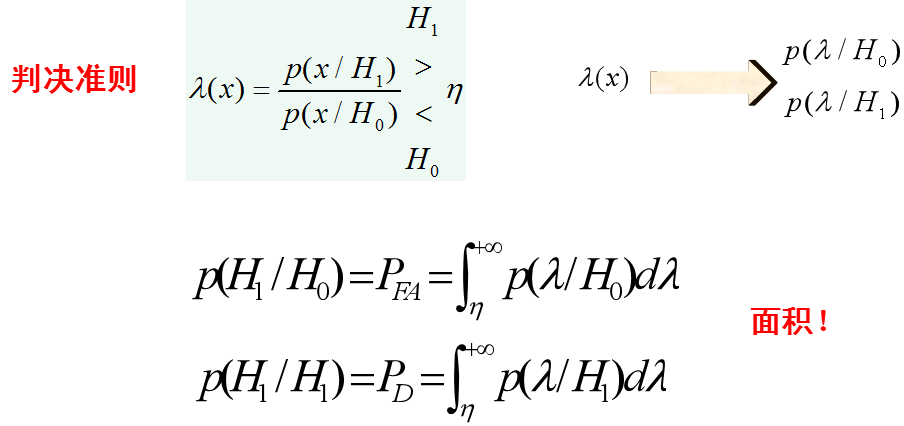
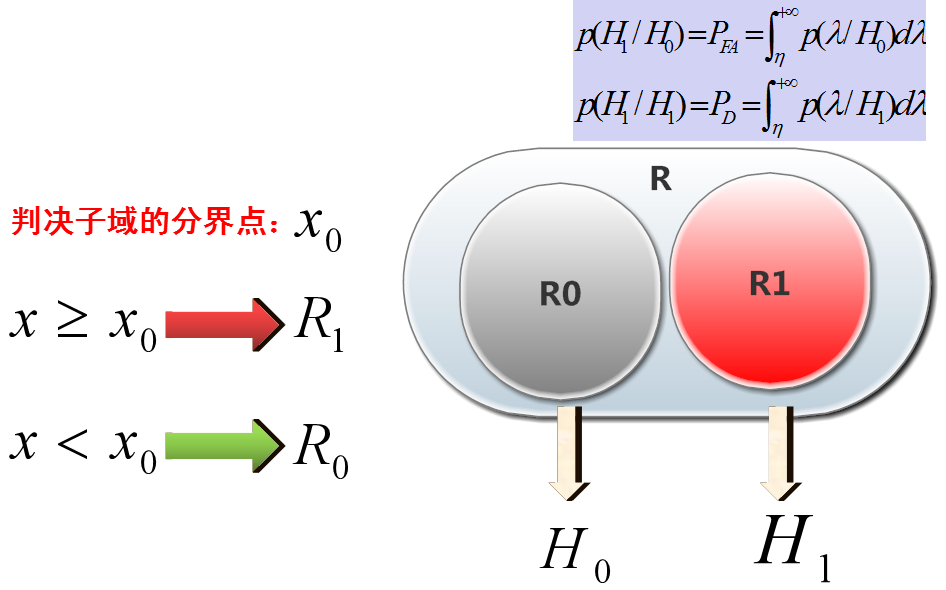
似然比檢測科等效為將接收信號的全域R劃分為兩個判決子域R0和R1,當接收信號x落入R0時,則判決假設H0成立,當接收信號x落入R1時則判決假設H1成立。
假設判決 有目標R1-H1,沒有目標R0-H0
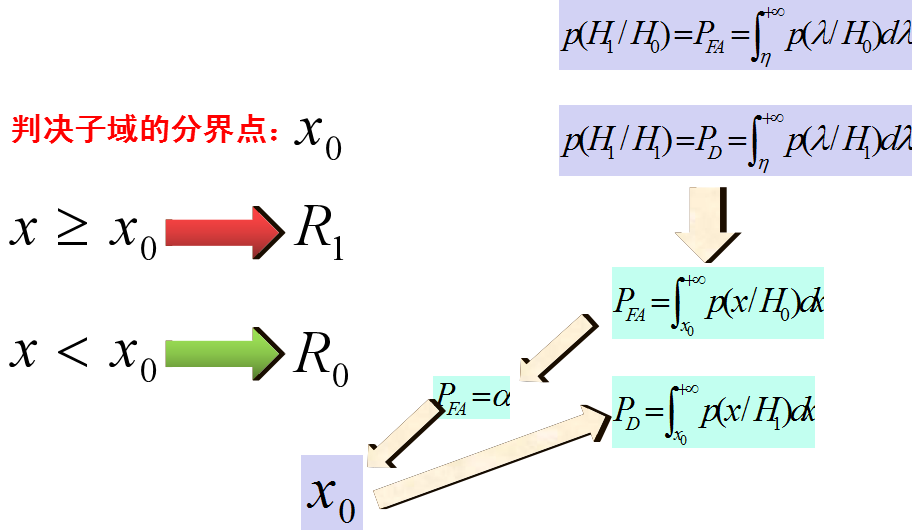

x為干擾信號幅度,sigma平方為窄帶高斯干擾信號方差,大小代表干擾信號強弱,當信號檢測門限為想0時,虛警概率為上式表示。

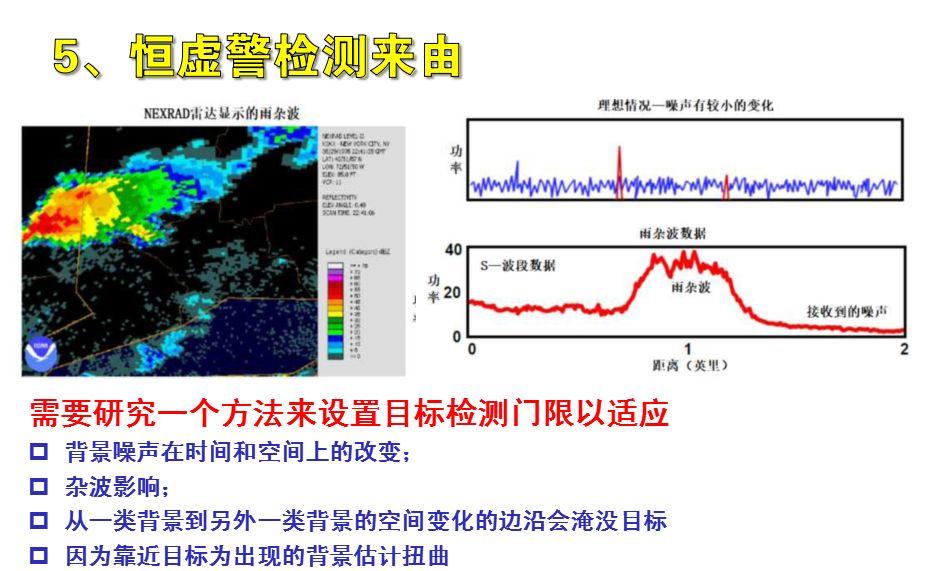
因此必須采取使虛警概率保持恒定的措施,即恒虛警處理技術,以實現雷達目標回波信號的恒虛警檢測!




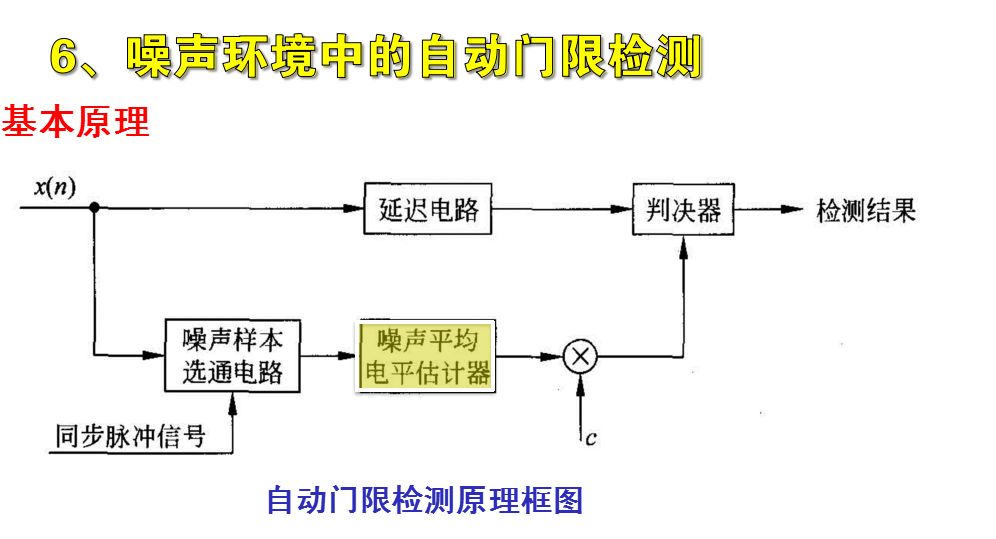
噪聲環境中信號的自動門限檢測,關鍵是自動形成與噪聲干擾環境相匹配的自動門限檢測電平。噪聲平均估計器和乘系數組成。

歸一化后,變量u的分布于噪聲強度沒有關系,對u用固定門限檢測就不會因為噪聲強度改變而引起虛警概率的變化啦。
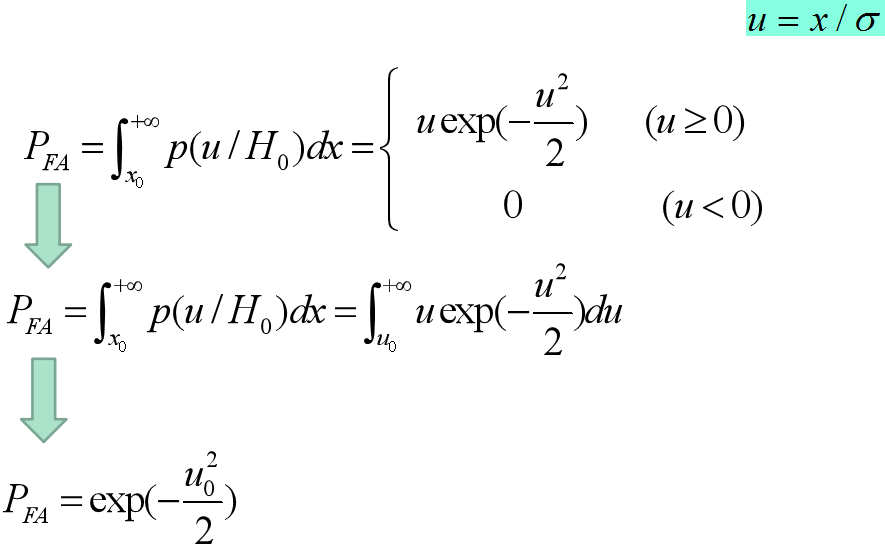
問題的關鍵就是求出噪聲干擾的標準差,并進行規劃處理,然后就可以固定門限檢測了,這時候虛警概率取決于檢測門限u0.
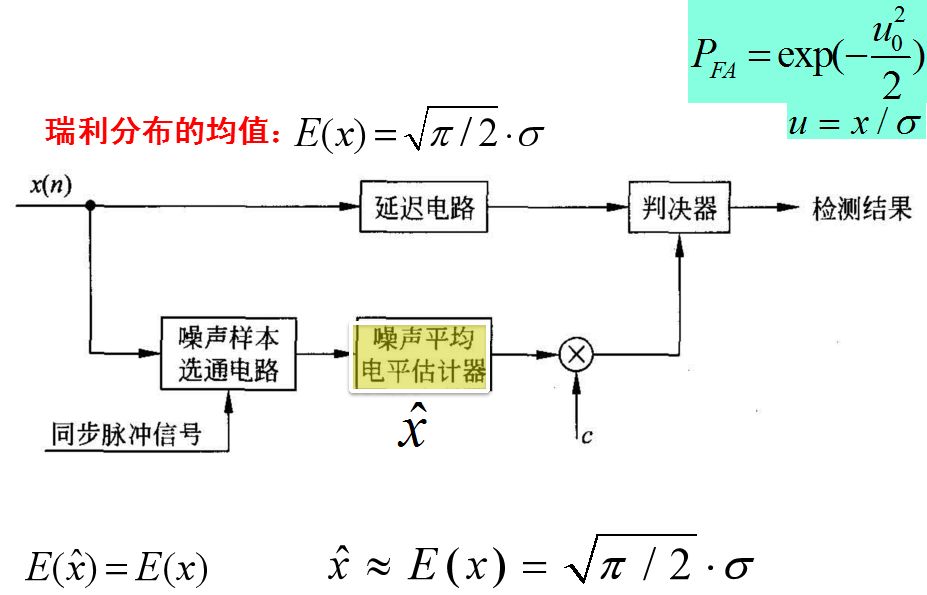
只要求出均值,就可以求出sigma。實現歸一化啦。噪聲平均電平估計器完成對x(n)求平均,得到噪聲的電平的估計值。
只要參與求噪聲電平估計的樣本數足夠多,估計值得均方誤差就會足夠小,估計值就會非常接近平均值E(x)。得到x的估值后乘以系數C,所形成的門限電平將隨著噪聲干擾強度的變化而變化,從而實現噪聲環境中信號的恒虛警檢測。
無論是什么的檢測方法,其本質上都是進行噪聲電平估計和乘系數c的計算。
審核編輯:湯梓紅
-
天線
+關注
關注
68文章
3196瀏覽量
140782 -
噪聲
+關注
關注
13文章
1120瀏覽量
47400 -
雷達
+關注
關注
50文章
2930瀏覽量
117465 -
信號檢測
+關注
關注
3文章
105瀏覽量
24959
原文標題:雷達回波信號檢測基礎
文章出處:【微信號:CloudBrain-TT,微信公眾號:云腦智庫】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
汽車雷達回波發生器的技術原理和應用場景
雷達回波信號FPGA程序設計的問題
雷達回波發生器的主要技術指標有什么?
如何利用FPGA構建一種通用的雷達回波信號實時模擬系統?
存在感應雷達感應模塊,人體回波特征探測雷達,飛睿科技雷達模組應用
一種雷達回波信號模擬器的設計與實現
基于PCI9820的雷達回波信號實時采集系統
電容的基礎知識和檢測方法

導航雷達回波信號的實時采集與回放
FPGA+DSP的雷達回波發生器設計解析





 雷達回波信號檢測基礎知識
雷達回波信號檢測基礎知識










評論