本文介紹了一項近似注意力機制新研究，耶魯大學、谷歌研究院等機構提出了 HyperAttention，使 ChatGLM2 在 32k 上下文長度上的推理時間快了 50%。

Transformer 已經成功應用于自然語言處理、計算機視覺和時間序列預測等領域的各種學習任務。雖然取得了成功，但這些模型仍面臨著嚴重的可擴展性限制，原因是對其注意力層的精確計算導致了二次（在序列長度上）運行時和內存復雜性。這對將 Transformer 模型擴展到更長的上下文長度帶來了根本性的挑戰。

業界已經探索了各種方法來解決二次時間注意力層的問題，其中一個值得注意的方向是近似注意力層中的中間矩陣。實現這一點的方法包括通過稀疏矩陣、低秩矩陣進行近似，或兩者的結合。

然而，這些方法并不能為注意力輸出矩陣的近似提供端到端的保證。這些方法旨在更快地逼近注意力的各個組成部分，但沒有一種方法能提供完整點積注意力的端到端逼近。這些方法還不支持使用因果掩碼，而因果掩碼是現代 Transformer 架構的重要組成部分。最近的理論邊界表明，在一般情況下，不可能在次二次時間內對注意力矩陣進行分項近似。

不過，最近一項名為 KDEFormer 的研究表明，在注意力矩陣項有界的假設條件下，它能在次二次時間內提供可證明的近似值。從理論上講，KDEFormer 的運行時大約為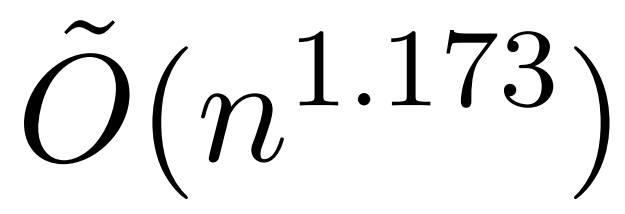；它采用核密度估計 (kernel density estimation,KDE) 來近似列范數，允許計算對注意力矩陣的列進行采樣的概率。然而，目前的 KDE 算法缺乏實際效率，即使在理論上，KDEFormer 的運行時與理論上可行的 O (n) 時間算法之間也有差距。

在文中，作者證明了在同樣的有界條目假設下，近線性時間的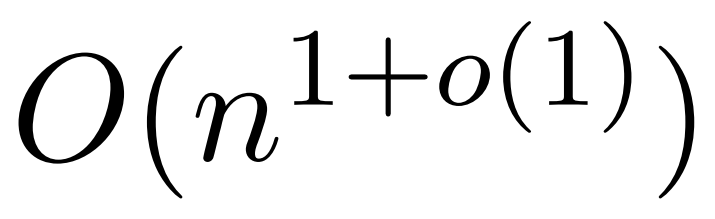算法是可能的。不過，他們的算法還涉及使用多項式方法來逼近 softmax，很可能不切實際。

而在本文中，來自耶魯大學、谷歌研究院等機構的研究者提供了一種兩全其美的算法，既實用高效，又是能實現最佳近線性時間保證。此外，該方法還支持因果掩碼，這在以前的工作中是不可能實現的。

論文標題：HyperAttention: Long-context Attention in Near-Linear Time

論文鏈接：

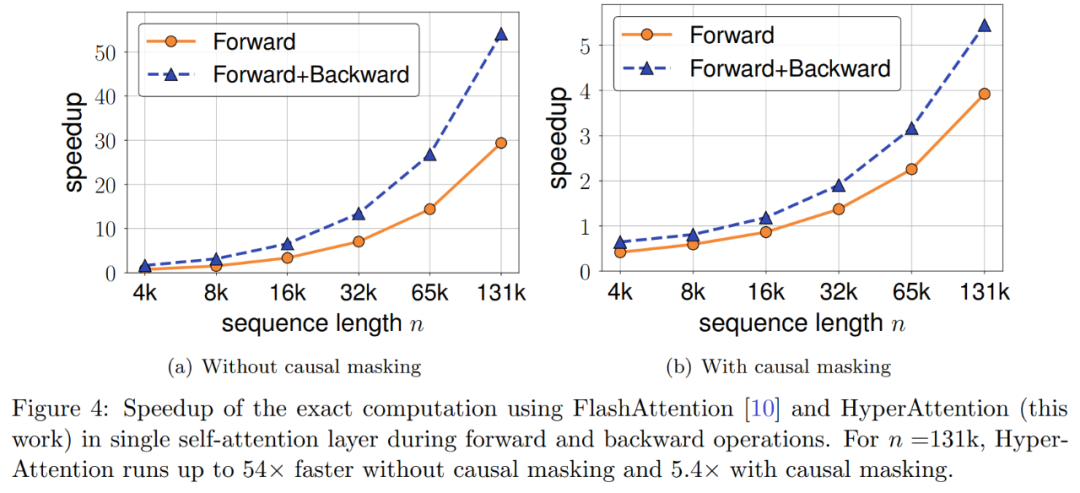
https://arxiv.org/abs/2310.05869 本文提出一種名為「HyperAttention」近似注意力機制，以解決大型語言模型中使用的長上下文日益復雜帶來的計算挑戰。最近的工作表明，在最壞情況下，除非注意力矩陣的條目有界或矩陣的穩定秩較低，否則二次時間是必要的。 研究者引入了兩個參數來衡量：（1）歸一化注意力矩陣中的最大列范數，（2）檢測和刪除大條目后，非歸一化注意力矩陣中的行范數的比例。他們使用這些細粒度參數來反映問題的難易程度。只要上述參數很小，即使矩陣具有無界條目或較大的穩定秩，也能夠實現線性時間采樣算法。 HyperAttention 的特點是模塊化設計，可以輕松集成其他快速底層實現，特別是 FlashAttention。根據經驗，使用 LSH 算法來識別大型條目，HyperAttention 優于現有方法，與 FlashAttention 等 SOTA 解決方案相比，速度有了顯著提高。研究者在各種不同的長上下文長度數據集上驗證了 HyperAttention 的性能。 例如，HyperAttention 使 ChatGLM2 在 32k 上下文長度上的推理時間快了 50%，而困惑度從 5.6 增加到 6.3。更大的上下文長度（例如 131k）和因果掩碼情況下，HyperAttention 在單個注意力層上速度提升了 5 倍。

方法概覽

點積注意涉及處理三個輸入矩陣: Q (queries) 、K (key)、V (value)，大小均為 nxd，其中 n 是輸入序列中的 token 數，d 是潛在表征的維度。這一過程的輸出結果如下: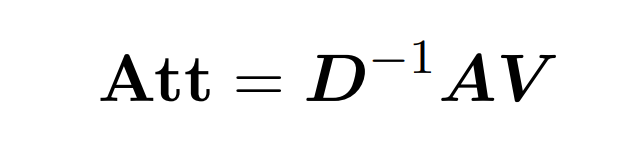 這里，矩陣 A := exp （QK^T) 被定義為 QK^T 的元素指數。D 是一個 n×n 對角矩陣，由 A 各行之和導出， 這里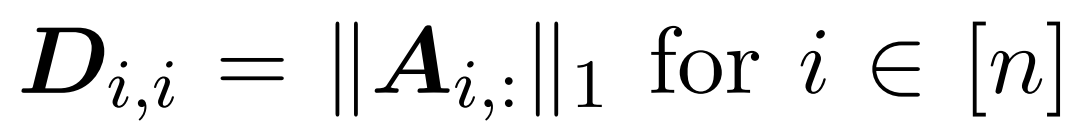。在這種情況下，矩陣 A 被稱為「注意力矩陣」，（D^-1 ) A 被稱為「softmax 矩陣」。值得注意的是，直接計算注意力矩陣 A 需要 Θ（n2d）運算，而存儲它需要消耗 Θ（n2）內存。因此，直接計算 Att 需要 Ω（n2d）的運行時和 Ω（n2）的內存。 研究者目標是高效地近似輸出矩陣 Att，同時保留其頻譜特性。他們的策略包括為對角縮放矩陣 D 設計一個近線性時間的高效估計器。此外，他們通過子采樣快速逼近 softmax 矩陣 D^-1A 的矩陣乘積。更具體地說，他們的目標是找到一個具有有限行數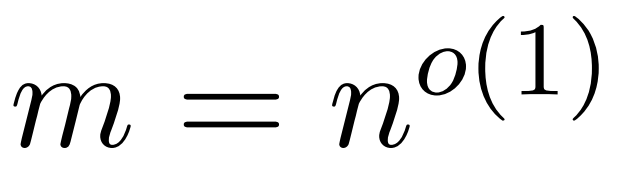的采樣矩陣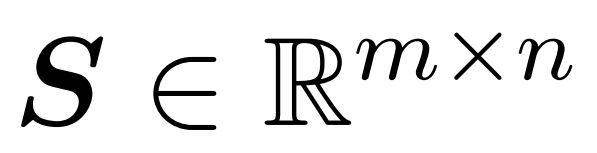以及一個對角矩陣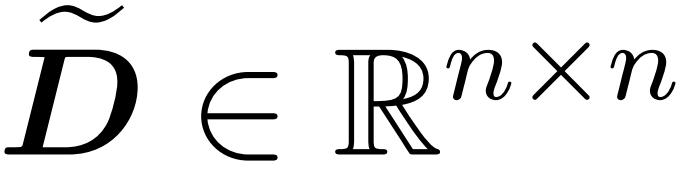，從而滿足誤差的算子規范的以下約束:

研究者表明，通過基于 V 的行規范定義采樣矩陣 S，可以高效解決公式 (1) 中注意力近似問題的矩陣乘法部分。更具挑戰性的問題是：如何獲得對角矩陣 D 的可靠近似值。在最近的成果中，Zandieh 有效地利用了快速 KDE 求解器來獲得 D 的高質量近似值。研究者簡化了 KDEformer 程序，并證明均勻采樣足以實現所需的頻譜保證，而無需基于內核密度的重要性采樣。這一重大簡化使他們開發出了一種實用的、可證明的線性時間算法。 與之前的研究不同，本文方法并不需要有界條目或有界穩定秩。此外，即使注意力矩陣中的條目或穩定秩很大，為分析時間復雜性而引入的細粒度參數仍可能很小。 因此，HyperAttention 的速度有了顯著提高，在序列長度為 n= 131k 時，前向和后向傳播速度提高了 50 倍以上。在處理因果掩碼時，該方法仍能大幅提高 5 倍的速度。此外，當該方法應用于預訓練的 LLM (如 chatqlm2-6b-32k ）并在長語境基準數據集 LongBench 上進行評估時，即使不需要微調，也能保持與原始模型接近的性能水平。研究者還對特定任務進行了評估，他們發現總結和代碼完成任務比問題解答任務對近似注意力層的影響更大。

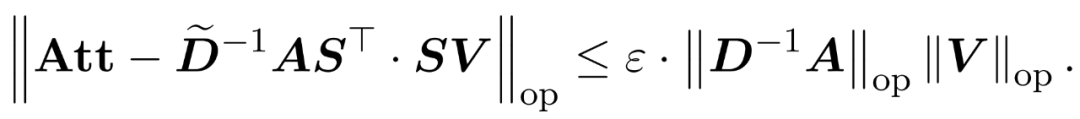
算法

為了在近似 Att 時獲得頻譜保證，本文第一步是對矩陣 D 的對角線項進行 1 ± ε 近似。隨后，根據 V 的平方行??-norms，通過采樣逼近 （D^-1）A 和 V 之間的矩陣乘積。 近似 D 的過程包括兩個步驟。首先，使用植根于 Hamming 排序 LSH 的算法來識別注意力矩陣中的主要條目，如定義 1 所示。第二步是隨機選擇一小部分 K。本文將證明，在矩陣 A 和 D 的某些溫和假設條件下，這種簡單的方法可以建立估計矩陣的頻譜邊界。研究者的目標是找到一個足夠精確的近似矩陣 D，滿足:

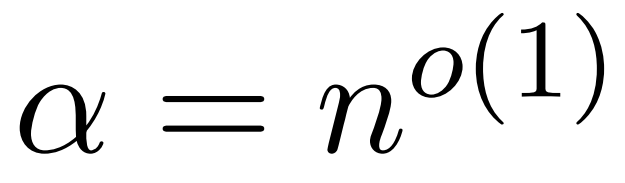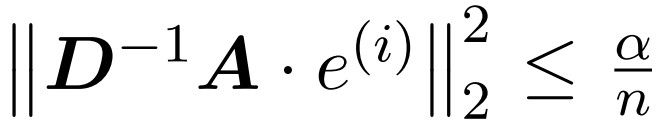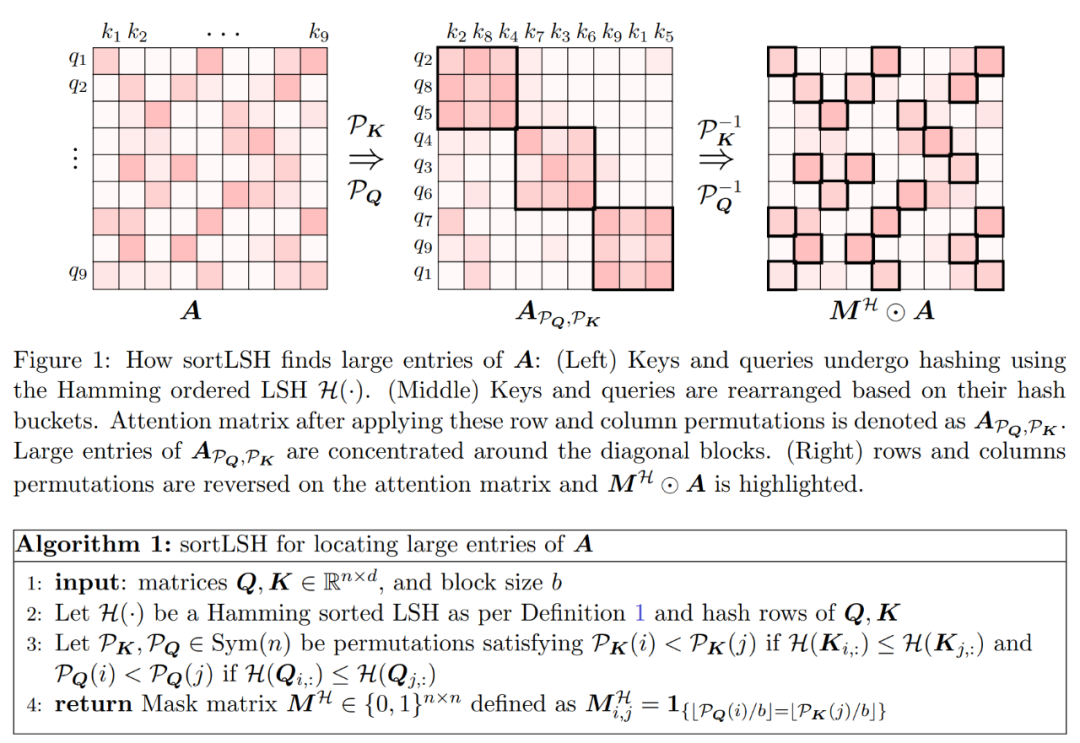
本文的假設是，softmax 矩陣的列范數呈現出相對均勻的分布。更準確地說，研究者假設對于任意 i ∈ [n] t 存在某個，使得。 算法的第一步是使用 Hamming 排序 LSH (sortLSH) 將鍵和查詢散列到大小均勻的桶中，從而識別注意力矩陣 A 中的大型條目。算法 1 詳細介紹了這一過程，圖 1 直觀地說明了這一過程。

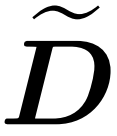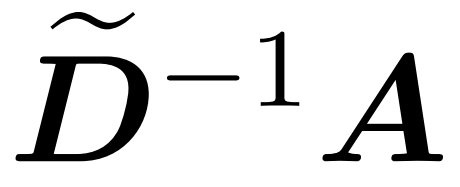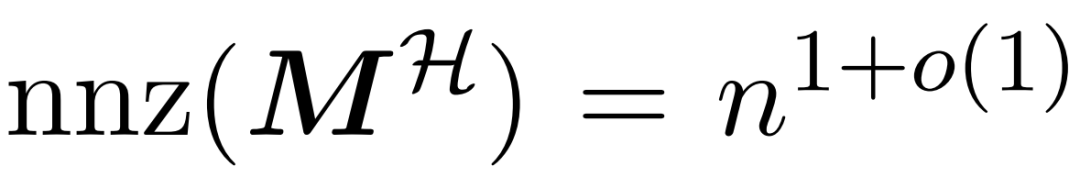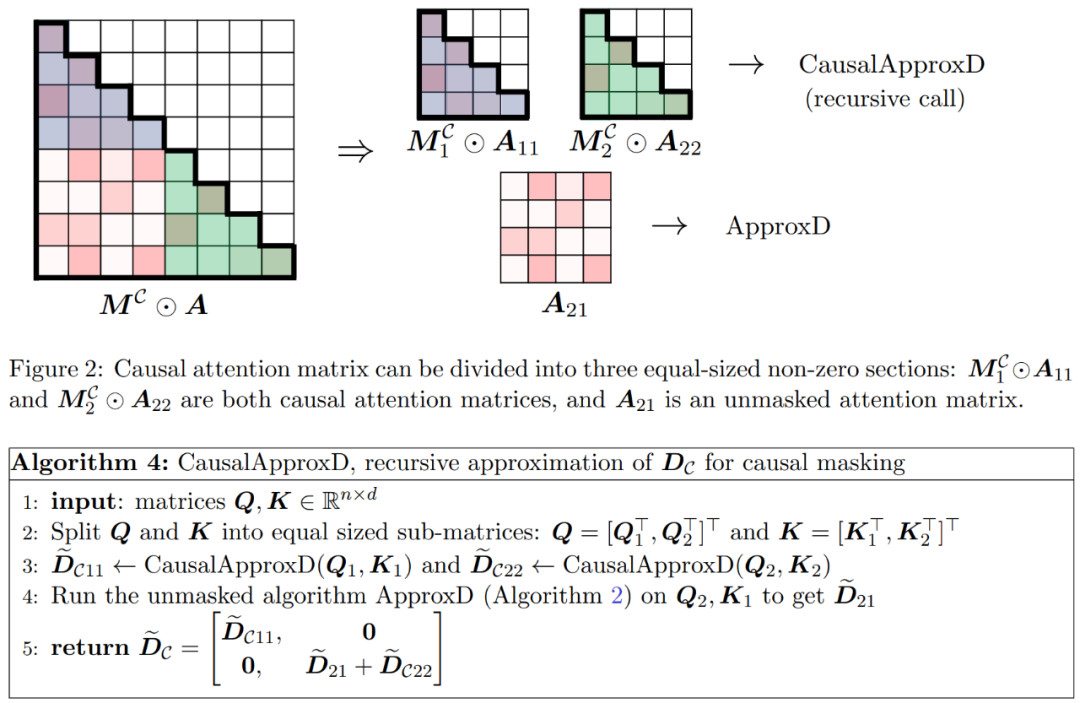
算法 1 返回一個稀疏掩碼，旨在隔離注意力矩陣的主要條目。給定該掩碼后，研究員在算法 2 中計算矩陣 D 的近似值，該近似值滿足公式 (2) 中的頻譜保證。該算法通過將掩碼對應的注意力值與注意力矩陣中隨機選擇的列子集相結合來實現。本文算法用途廣泛，可以有效地使用預定義的掩碼，該掩碼指定了注意力矩陣中主要條目的位置。本算法提供的主要保證在定理 1 中給出。 ?整合近似對角線和近似與值矩陣 V 之間矩陣乘積的子程序。因此，研究者引入了 HyperAttention，這是一種高效算法，可以在近似線性時間內近似公式（1）中具有頻譜保證的注意力機制。算法 3 將定義注意力矩陣中主導條目的位置的掩碼 MH 作為輸入。這個掩碼可以使用 sortLSH 算法（算法 1）生成，也可以是一個預定義的掩碼，類似于 [7] 中的方法。研究者假定大條目掩碼 M^H 在設計上是稀疏的，而且其非零條目數是有界的。 如圖 2 所示，本文方法基于一個重要的觀察結果。屏蔽注意力 M^C⊙A 可以分解成三個非零矩陣，每個矩陣的大小是原始注意力矩陣的一半。完全位于對角線下方的 A_21 塊是未屏蔽注意力。因此，我們可以使用算法 2 近似計算其行和。 圖 2 中顯示的兩個對角線區塊和是因果注意力，其大小只有原來的一半。為了處理這些因果關系，研究者采用遞歸方法，將它們進一步分割成更小的區塊，并重復這一過程。算法 4 中給出了這一過程的偽代碼。

實驗及結果

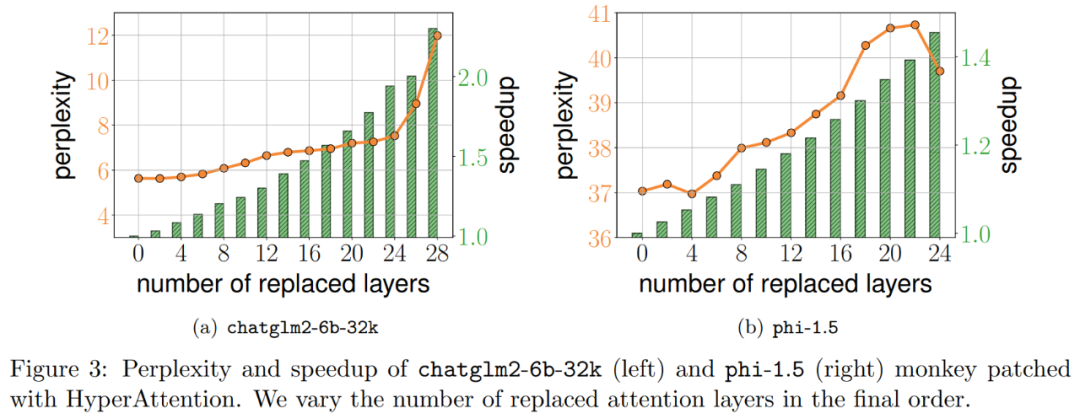
研究者通過擴展現有大語言模型來處理 long range 序列，進而對算法進行基準測試。所有實驗都在單個 40GB 的 A100 GPU 上運行，并用 FlashAttention 2 來進行精確的注意力計算。 Monkey Patching自注意力 研究者首先在兩個預訓練 LLM 上評估 HyperAttention，選擇了實際應用中廣泛使用的具有不同架構的兩個模型：chatglm2-6b-32k 和 phi-1.5。 在操作中，他們通過替換為 HyperAttention 來 patch 最終的?注意力層，其中?的數量可以從 0 到每個 LLM 中所有注意力層的總數不等。請注意，兩個模型中的注意力都需要因果掩碼，并且遞歸地應用算法 4 直到輸入序列長度 n 小于 4,096。對于所有序列長度，研究者將 bucket 大小 b 和采樣列數 m 均設置為 256。他們從困惑度和加速度兩個方面評估了這類 monkey patched 模型的性能。 同時研究者使用了一個長上下文基準數據集的集合 LongBench，它包含了 6 個不同的任務，即單 / 多文檔問答、摘要、小樣本學習、合成任務和代碼補全。他們選擇了編碼序列長度大于 32,768 的數據集的子集，并且如果長度超過 32,768，則進行剪枝。接著計算每個模型的困惑度，即下一個 token 預測的損失。為了突出長序列的可擴展性，研究者還計算所有注意力層的總加速，無論是由 HyperAttention 還是 FlashAttention 執行。 結果如下圖 3 所示，即使經過 HyperAttention 的 monkey patch，chatglm2-6b-32k 仍顯示出合理的困惑度。例如替換 20 層后，困惑度大約增加了 1，并在達到 24 層之前繼續緩慢增加。注意力層的運行時提升了大約 50%。如果所有層都被替換，則困惑度上升到 12，運行速度提升 2.3。phi-1.5 模型也表現出了類似的情況，但隨著 HyperAttention 數量的增加，困惑度會線性增長。

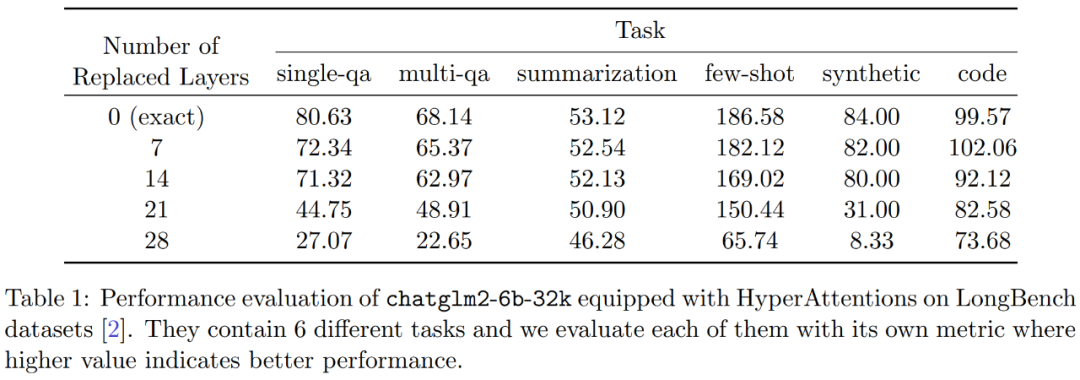
此外，研究者評估了 LongBench 數據集上 monkey patched chatglm2-6b-32k 的性能，并計算單 / 多文檔問答、摘要、小樣本學習、合成任務和代碼補全等各自任務上的評估分數。結果如下表 1 所示。 雖然替換 HyperAttention 通常會導致性能下降，但他們觀察到它的影響會基于手頭任務發生變化。例如，摘要和代碼補全相對于其他任務具有最強的穩健性。

顯著的一點是，當半數注意力層（即 14 層）被 patch 之后，研究者證實了大多數任務的性能下降幅度不會超過 13%。尤其是摘要任務，其性能幾乎保持不變，表明該任務對注意力機制中的部分修改具有最強的穩健性。當 n=32k 時，注意力層的計算速度提升了 1.5 倍。 單個自注意力層 研究者進一步探索了序列長度從 4,096 到 131,072 不等時，HyperAttention 的加速度。他們測量了當使用 FlashAttention 計算或通過 HyperAttention 加速時，前向和前向 + 后向操作的掛鐘時間。此外還測量了有或沒有因果掩碼時的掛鐘時間。所有輸入 Q、K 和 V 的長度相同，維數固定為 d = 64，注意力頭數量為 12。 他們在 HyperAttention 中選擇與前文相同的參數。如下圖 4 所示，HyperAttention 在沒有應用因果掩碼時速度提升 54 倍，用了之后速度提升 5.4。盡管因果掩碼和非掩碼的時間困惑度相同，但因果掩碼的實際算法（算法 1）需要額外的操作，例如分區 Q、K 和 V、合并注意力輸出，從而導致實際運行時增加。當序列長度 n 增加時，加速度會更高。 研究者認為，不僅對于推理，而且對于訓練或微調 LLM 以適應更長的序列，這些結果為擴展自注意力打開了大門。

?