濾波是信號分析與處理中常用的一種手段,用以濾除信號中不需要的頻率成分或提高信噪比。傳統的濾波是在頻域上實現的,通過對信號作Fourier變換得到信號的頻域表示后,根據頻率的分布情況,采用某種結構的濾波器按照一定的技術要求將欲去除的成分濾除。
然而,對于非線性和非平穩信號,頻域濾波方法面臨著很大的困難,因為利用Fourier變換很難得到這類信號的真實頻譜,它們在頻域上常常表現為許多的諧波成分,從而使得濾波后的信號失真。
現代濾波理論把信號和噪聲都視為隨機信號,利用它們的統計特征(如自相關函數、功率譜等)導出一套最佳的估值算法,從含有噪聲的信號中估計出信號的某些特征或信號本身,以此來提高信號的信噪比。
維納濾波法是現代濾波理論中的典型代表,其基本思想是在已知信號和噪聲的相關函數或功率譜密度的條件下,通過求解積分方程,在最小均方誤差意義上實現信號的最佳線性估計。
維納濾波本質上是一種頻域方法,只適用于單輸入單輸出的平穩隨機信號,并且需要噪聲和有用信號的先驗知識,但是在實際中,這些先驗知識很難得到或者過于簡化,從而使得理論上最優的維納濾波達不到要求。
(1)小波濾波
小波濾波是近十幾年來小波變換在信號分析與處理領域中的一個重要應用方面,其基本原理是將含噪聲的信號經過小波變換后,利用具體問題的先驗知識,根據信號系數和噪聲系數在不同尺度上具有不同性質的機理,構造相應的規則,在小波域對含噪信號的系數進行處理,目的在于減小甚至完全剔除噪聲系數,同時最大限度地保留信號系數,得到真實信號的最優估計。
總的來說,小波濾波過程一般由三個步驟完成:小波變換、對小波系數非線性處理以濾除噪聲和小波逆變換。
在對信號進行小波變換時,小波基的選取是一個非常關鍵的問題。理想的小波基應具有對稱性、緊支撐,高消失矩和正交性,但要使一個小波基同時具有這些性質往往不現實,因此在應用中只能根據具體要求選擇合適的小波基。
隨著小波濾波理論研究的深入,若能做到按信號特征自適應選擇小波基,則信號描述的效果將會得到較大的改善。
(2)EMD濾波
EMD將信號從高頻至低頻分解為若干階IMF,整個過程體現了多尺度的濾波過程。借助這一點,我們可以方便地構造一種新型的濾波方式,即根據信號分析的目的,有選擇性地把不同的IMF組合起來,以突出信號在某一頻率范圍內的特征。
顯然,去掉先分解出來的幾階IMF,把其余的IMF和殘余項組合起來,相當于原信號通過了一個低通濾波器;去掉最后分解出來的幾階IMF和殘余項,把其余的IMF組合起來,相當于原信號通過了一個高通濾波器;去掉最先和最后分解出來的幾階IMF和殘余項,只組合中間部分的IMF,相當于原信號通過了一個帶通濾波器;去掉中間部分的IMF,將最先和最后分解出來的幾階IMF和殘余項組合起來,相當于原信號通過了一個帶阻濾波器。
這種基于EMD的濾波技術的優勢是濾波后的結果能夠充分保留信號的非線性和非平穩性信息,重新組合的信號不會對原信號的固有特性造成扭曲。
此外,由于EMD是依據信號的局部特征時間尺度分解的,是一種后驗的分解方法,因此這種濾波方式自適應性較強,對信號類型幾乎沒有限制,不需要定義濾波器參數,受主觀因素影響很小,是一種完全的數據驅動算法,簡單易行,并且在多數情況下都可以達到滿意的效果。
圖1所示為含有高頻衰減隨機噪聲干擾和低頻趨勢項的仿真信號,這是一個典型的非平穩信號,若用傳統的濾波方法是很難將噪聲和趨勢項較好剔除的,而根據EMD的濾波特性對該信號進行濾波則可得到很好的效果。
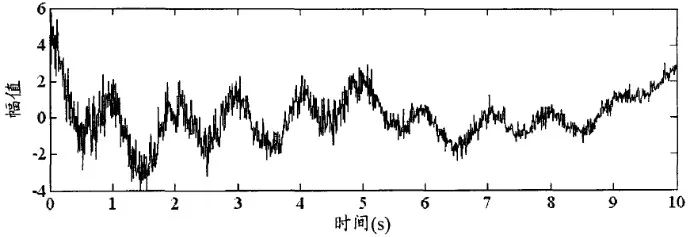
圖1 含有高頻衰減隨機噪聲和低頻趨勢項的信號
圖2中的實線所示為利用該仿真信號的第七階和第八階IMF重構的結果,點線所示為相應的真實值,可以看到兩條曲線非常接近。

圖2 利用EMD濾波后的結果與真實值的比較
-
信噪比
+關注
關注
3文章
262瀏覽量
28969 -
衰減器
+關注
關注
4文章
717瀏覽量
34939 -
EMD
+關注
關注
1文章
43瀏覽量
20279 -
小波濾波器
+關注
關注
0文章
4瀏覽量
6058 -
信號濾波
+關注
關注
0文章
21瀏覽量
7721
發布評論請先 登錄


















評論