01
中值濾波
原理
中值濾波是一種非線性濾波算法,它將信號中的每個采樣點替換成該采樣點鄰域內的中值。它的主要思想是通過找到鄰域內的中值來消除信號中的噪聲,同時盡可能地保留信號中的有用信息。
中值濾波的步驟如下:
a. 定義鄰域大小和形狀。常用的鄰域形狀有矩形、圓形、十字形等。
b. 對信號的每個采樣點,選取其鄰域內的所有采樣點,并將其排序。
c. 將排序后的采樣點序列中間的值作為該采樣點的輸出值。
由于中值濾波采用了排序的方式,因此它比線性濾波算法的計算量要大,但是相對于其它非線性濾波算法,中值濾波的計算量相對較小,而且不需要預先確定濾波器參數,因此具有很好的實時性能。
中值濾波通常適用于以下場景:
a. 信號中含有脈沖噪聲或椒鹽噪聲。
b. 信號中含有高斯噪聲,但信號的均值和方差不易確定。
c. 信號中含有周期性噪聲,周期長度大于鄰域大小。
需要注意的是,中值濾波可能會導致信號的某些特征被模糊化,因此在應用中需要謹慎選擇鄰域大小和形狀,以及濾波器的使用場景。
代碼
下面是一個使用C語言編寫的中值濾波函數的示例代碼,它可以處理一個長度為N的整型數組input,并將輸出結果保存在一個長度為N的整型數組output中。這個函數的鄰域大小由變量size指定,可以根據需要進行調整。
C++
#include
#include
#define SIZE 3 // 鄰域大小
int cmp(const void *a, const void b) {
return ( (int *)a - *(int *)b);
}
void median_filter(int *input, int *output, int N) {
int i, j, k, m;
int median[SIZE * SIZE];
for (i = 0; i < N; i++) {
k = 0;
for (j = i - (SIZE - 1) / 2; j <= i + (SIZE - 1) / 2; j++) {
if (j < 0 || j >= N) {
continue;
}
for (m = j - (SIZE - 1) / 2; m <= j + (SIZE - 1) / 2; m++) {
if (m < 0 || m >= N) {
continue;
}
median[k++] = input[m];
}
}
qsort(median, k, sizeof(int), cmp);
output[i] = median[k / 2];
}
}
int main() {
int input[] = {1, 5, 2, 7, 3, 9, 4, 8, 6};
int output[sizeof(input) / sizeof(int)];
int N = sizeof(input) / sizeof(int);
int i;
median_filter(input, output, N);
printf("Input data: ");
for (i = 0; i < N; i++) {
printf("%d ", input[i]);
}
printf("n");
printf("Output data: ");
for (i = 0; i < N; i++) {
printf("%d ", output[i]);
}
printf("n");
return 0;
}
輸出結果如下:
Kotlin
Input data: 1 5 2 7 3 9 4 8 6
Output data: 2 2 3 4 4 5 6 7 8
可以看到,中值濾波算法可以有效地消除噪聲,同時盡可能地保留原始信號的特征。需要注意的是,在使用中值濾波算法時,鄰域大小的選擇需要根據實際情況進行調整,以免產生過度平滑或者信息損失的問題。
02
消抖濾波
原理
消抖濾波法(Debouncing Filter)是一種常用的信號處理算法。它主要用于消除由于輸入信號在短時間內出現了快速變化而導致的抖動現象。在實際應用中,如電子開關、按鍵等場景中,由于機械接觸的原因,可能會產生短時間內快速變化的信號,這種信號稱為抖動信號,會對系統產生誤判和誤動作。因此,需要對這種信號進行濾波處理。
消抖濾波法的基本思想是在輸入信號發生變化時,延遲一段時間再檢測信號狀態,如果信號保持穩定狀態,則認為信號有效。如果信號在這段時間內發生了變化,則重新計時。這種方法可以有效地抑制抖動信號,并且可以消除無效的信號瞬態。
消抖濾波法的具體實現方式可以采用軟件或硬件的方式實現。軟件實現方式常見的是利用定時器進行延時,硬件實現方式常見的是利用RC電路進行延時。下面給出一個基于軟件實現的消抖濾波函數的偽代碼:
Python
int debouncing_filter(int input, int delay_ms) {
static int last_input = 0;
static int stable_cnt = 0;
if (input != last_input) {
stable_cnt = 0;
}
else {
stable_cnt++;
}
last_input = input;
if (stable_cnt >= delay_ms / sampling_time) {
return input;
}
else {
return last_input;
}
}
在這個函數中,input表示輸入信號的狀態,delay_ms表示需要延遲的時間。函數通過記錄上一個時刻的輸入狀態以及信號保持穩定狀態的時間來實現消抖功能。如果信號保持穩定狀態的時間超過了設定的延時時間,則返回當前的輸入狀態。否則,返回上一個時刻的輸入狀態。
需要注意的是,在使用消抖濾波法時,延時時間需要根據具體的應用場景來進行設置。如果延時時間設置過長,則可能會導致信號響應時間過長,影響系統的實時性;如果延時時間設置過短,則可能會無法有效地抑制抖動信號。
代碼
下面給出一個基于軟件實現的消抖濾波函數的具體實現代碼,以及使用示例:
C++
int debouncing_filter(int input, int delay_ms) {
static int last_input = 0;
static int stable_cnt = 0;
if (input != last_input) {
stable_cnt = 0;
}
else {
stable_cnt++;
}
last_input = input;
if (stable_cnt >= delay_ms / 10) { // 采樣周期假設為10ms
return input;
}
else {
return last_input;
}
}
在這個函數中,input表示輸入信號的狀態,delay_ms表示需要延遲的時間。函數通過記錄上一個時刻的輸入狀態以及信號保持穩定狀態的時間來實現消抖功能。如果信號保持穩定狀態的時間超過了設定的延時時間,則返回當前的輸入狀態。否則,返回上一個時刻的輸入狀態。
下面給出一個示例,展示如何使用該函數進行消抖處理:
C++
#include
int main() {
int input = 0;
int output = 0;
int delay_ms = 50; // 延時時間為50ms
while (1) {
scanf("%d", &input); // 從終端讀取輸入信號狀態
output = debouncing_filter(input, delay_ms); // 進行消抖濾波處理
printf("Input: %d, Output: %dn", input, output); // 輸出結果
}
return 0;
}
在這個示例中,首先從終端讀取輸入信號狀態,然后調用debouncing_filter函數進行消抖濾波處理,并將處理后的結果輸出到終端。循環執行該過程,直到程序結束。
03
遞推平均濾波
原理
遞推平均濾波法,又稱為滑動平均濾波法,是一種對于輸入信號進行平滑處理的算法。該算法采用一定的方式對一定數量的輸入信號進行加權平均,得到一個平滑的輸出信號。具體地,遞推平均濾波法使用一個固定長度的窗口,每當有新的輸入信號到來時,就將窗口內的舊的信號淘汰掉,并將新的信號加入到窗口中,然后重新計算窗口內所有信號的平均值作為當前的輸出信號。
因此,隨著新的信號不斷到來,窗口內的信號會不斷滑動,而輸出信號也會不斷變化,從而實現對輸入信號的平滑處理。
遞推平均濾波法的優點是簡單、實時性好,對于周期性的噪聲有一定的抑制效果。其缺點是在處理突變的輸入信號時,輸出信號會有一定的延遲,且在窗口大小不夠大的情況下,噪聲的抑制效果會比較有限。
下面是遞推平均濾波法的算法步驟:
a. 定義一個固定長度為N的窗口,并初始化窗口內的所有數據為0。
b. 當有新的輸入信號x_i到來時,將窗口內的第一個信號x_{i-N}移除,并將新的信號x_i加入到窗口中。
c. 計算窗口內所有信號的平均值,作為當前的輸出信號y_i。
d. 返回輸出信號y_i,并等待下一次輸入信號到來。
代碼
下面是遞推平均濾波法的示例代碼,其中,N為窗口大小,x表示輸入信號,y表示輸出信號,buffer為窗口緩存,sum為窗口內數據的累加和:
C++
#define N 10 // 窗口大小
float moving_average_filter(float x) {
static float buffer[N] = {0};
static float sum = 0;
static int ptr = 0;
sum = sum - buffer[ptr] + x;
buffer[ptr] = x;
ptr = (ptr + 1) % N;
return sum / N;
}
在這個函數中,我們使用了一個靜態的窗口緩存buffer來存儲窗口內的數據,使用sum來記錄窗口內數據的累加和,使用ptr來記錄當前窗口內最后一個數據的位置。當有新的輸入信號x到來時,我們將窗口內第一個數據buffer[ptr-N]移除,并將新的信號x加入到窗口中。然后,我們重新計算窗口內所有信號的平均值作為當前的輸出信號,并將作為當前的輸出信號,返回輸出信號,并等待下一次輸入信號到來。
04
中位值平均濾波法
原理
中位值平均濾波法是一種抗干擾性能很強的濾波方法,也稱為防脈沖干擾平均濾波法。與其他濾波方法不同的是,它不是對一段時間內的數據進行簡單的平均處理,而是將一段時間內的多個數據進行排序,然后取中間值作為濾波結果。中位值平均濾波法的優點是可以有效地濾除脈沖噪聲、斜坡干擾等干擾信號。
中位值平均濾波法的實現步驟如下:
a. 將一段時間內的多個數據存儲在數組中;
b. 對數組進行排序;
c. 取排序后中間位置的數值作為濾波結果。
中位值平均濾波法的實現較為簡單,但由于需要對數組進行排序,計算量較大,因此在實際應用中需要注意性能問題。
中位值平均濾波法的優點:
a. 對脈沖噪聲、斜坡干擾等干擾信號具有較強的濾除能力;
b. 濾波效果較好,能夠保持信號的較高精度。
中位值平均濾波法的缺點:
a. 計算量較大,特別是在大數據量時;
b. 無法完全消除高頻噪聲,因此在高頻噪聲較多的情況下效果可能不佳;
c. 數組排序會改變原始數據的順序,因此需要注意排序的實現方式,避免對實際應用造成影響。
代碼
C++
#include
// 中位值平均濾波函數
int Median_Filter(int *data, int length)
{
int i, j, temp, result;
int *sort = (int *)malloc(sizeof(int) * length); // 分配排序數組的空間
memcpy(sort, data, sizeof(int) * length); // 復制原始數據到排序數組
// 冒泡排序
for (i = 0; i < length - 1; i++) {
for (j = i + 1; j < length; j++) {
if (sort[i] > sort[j]) {
temp = sort[i];
sort[i] = sort[j];
sort[j] = temp;
}
}
}
// 取中間值作為濾波結果
result = sort[length / 2];
// 釋放排序數組的空間
free(sort);
return result;
}
int main()
{
int data[10] = {5, 6, 8, 9, 12, 7, 13, 10, 11, 6};
int result;
result = Median_Filter(data, 10);
printf("Filtered result: %dn", result);
return 0;
}
上面的程序實現了一個簡單的中位值平均濾波函數Median_Filter,該函數的參數data為原始數據數組,length為數據數組的長度。函數返回經過中位值平均濾波后的結果。
在main函數中,我們聲明了一個長度為10的原始數據數組data,并將其傳遞給Median_Filter函數進行中位值平均濾波。最后輸出濾波后的結果。
-
濾波器
+關注
關注
161文章
7843瀏覽量
178378 -
非線性濾波
+關注
關注
0文章
7瀏覽量
6745 -
中值濾波
+關注
關注
0文章
14瀏覽量
8389 -
高斯噪聲
+關注
關注
0文章
11瀏覽量
8377
發布評論請先 登錄
相關推薦
如何用單片機實現數字濾波?6種數字濾波算法解析
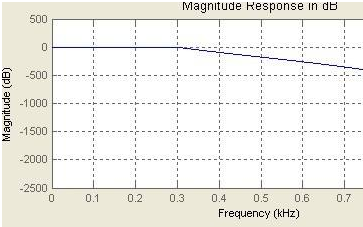
常見的濾波算法及其在單片機中的應用介紹(一)
單片機數據采集——數字濾波算法
如何用單片機實現數字濾波算法
使用51單片機實現MPU6050的卡爾曼濾波算法代碼免費下載
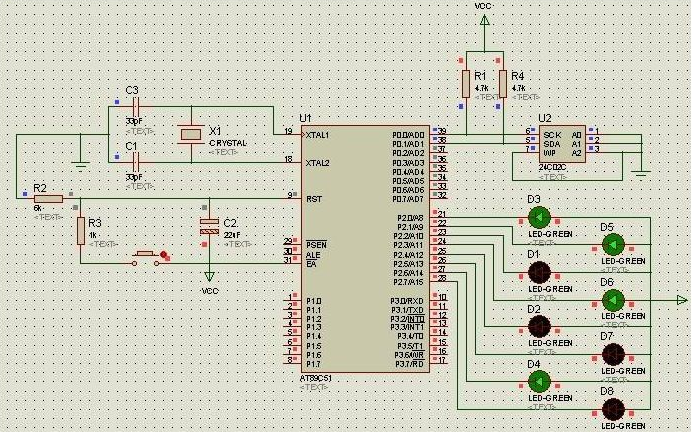
單片機中晶振電路的作用及常見參數的介紹
這篇把單片機數字濾波算法講絕了





 常見的濾波算法及其在單片機中的應用介紹(二)
常見的濾波算法及其在單片機中的應用介紹(二)










評論