道德經云:”道生一,一生二,二生三,三生萬物“。學習知識亦是如此,一個概念衍生出兩個概念,兩個概念演化出更小的子概念,接著衍生出整個知識體系。
筆者結合自己對統計學和概率論知識的理解寫了這篇文章,有以下幾個目標
目標一:構建出可以讓人理解的知識架構,讓讀者對這個知識體系一覽無余
目標二:盡l量闡述每個知識在數據分析工作中的使用場景及邊界條件
目標三:為讀者搭建從“理論”到“實踐“的橋梁
概述
你的“對象” 是誰?
此對象非彼“對象”,我們學習“概率和統計學”目的在于應用到對于“對象”的研究中,筆者將我們要研究的“對象”按照維度分為了兩大類。
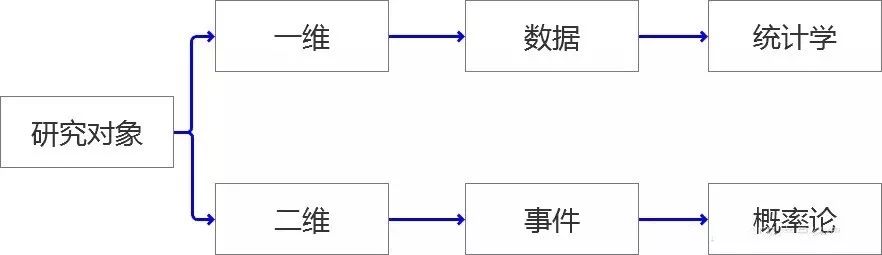
一維:就是當前擺在我們面前的“一組”,“一批”,哪怕是“一坨”數據。這里我們會用到統計學的知識去研究這類對象。
二維:就是研究某個“事件”,筆者認為事件是依托于“時間軸”存在的,過去是否發生,現在是可能會出現幾種情況,每種情況未來發生的可能性有多大?這類問題是屬于概率論的范疇。
因此,我們在做數據分析的研究前,先弄清我們研究的對象屬于哪類范疇,然后在按著這個分支檢索自己該用到的知識或方法來解決問題。
分析就像在給 “愛人” 畫肖像
從外觀的角度描述一個姑娘,一般是面容怎么樣?身段怎么樣?兩個維度去描述。就像畫一幅肖像畫,我們的研究“對象”在描述性分析中也是通過兩個維度去來描述即,“集中趨勢---代表值”,“分散和程度”。
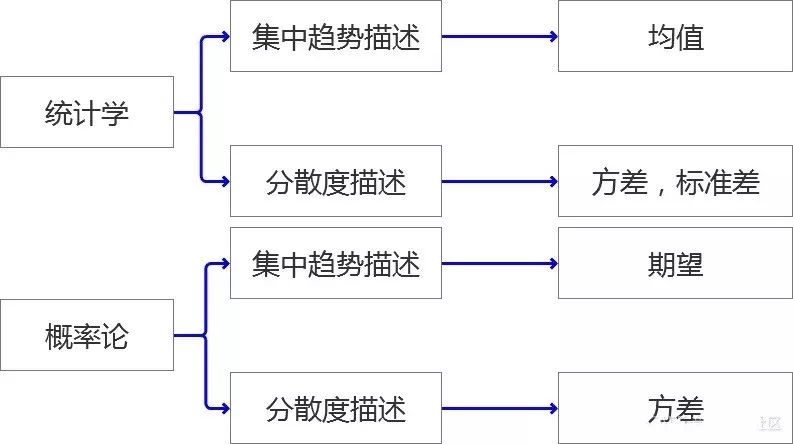
看到這幾個概念是不是就很熟悉了?筆者認為一個描述性的分析就是從這兩個維度來說清楚你要研究的對象是什么樣子?至于從哪些特征開始說呢?就是常用的概念“均值”,“方差”之類的。下面我們進入正題,筆者將詳細闡述整個知識架構。
01
對“數據”的描述性分析
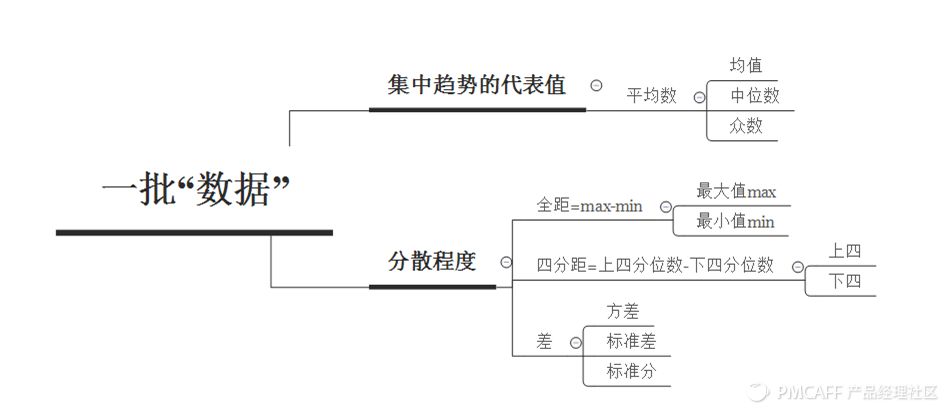
數據分析中最常規的情況,比如你手上有一組,一批或者一坨數據,數據分析的過程就是通過“描述”從這些數據中獲取的信息,通常可以從兩個維度去描述:
1. 集中趨勢量度:為這批數據找到它們的“代表”
均值(μ)
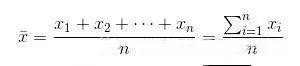
均值的局限性
均值是最常用的平均數之一,但是它的局限性在于“若用均值描述的數據中存在異常值的情況,會產生偏差” ;例如下面一組數據就不太適合用均值來代表
這5個人的年齡均值是:31.2歲

很顯然,在這組數據中,大部分人的年齡是10幾歲的青少年,但是E的年齡是100歲為異常值,用均值來描述他們的年齡是31.2歲,很顯然用均值作為描述這組數據是不合適的,那么我們該如何準確的表征這組數據呢???
中位數
中位數,又稱中點數,中值。是按順序排列的一組數據中居于中間位置的數。
中位數的局限

回到上一個例子,若用中位數來表征這組數據的平均年齡,就變得更加合理,中位數15。
那么我們在看一下下面一組數據,中位數的表現又如何?

中位數:45
這組數據的中位數為:45,但是中位數45并不能代表這組數據。
因為這組數據分為兩批,兩批的差異很大。那么如何處理這類數據呢?接下來介紹第三位平均數。
眾數
眾數是樣本觀測值在頻數分布表中頻數最多的那一組的組中值。
平均數可以表征一批數據的典型值,但是僅憑平均數還不能給我們提供足夠的信息,平均數無法表征一組數據的分散程度。
2. 分散性與變異性的量度
(全距,迷你距,四分位數,標準差,標準分)
全距=max-min
全距也叫“極差”極差。它是一組數據中最大值與最小值之差。可以用于度量數據的分散程度。
全距的局限性
全距雖然求解方便快捷,但是它的局限性在于“若數據中存在異常值的情況,會產生偏差。為了擺脫異常值帶來的干擾,比如我們看一下下面的兩組數據。只是增加了一個異常值,兩組數據的全距產生了巨大的差異。
四分位數
所有觀測值從小到大排序后四等分,處于三個分割點位置的數值就是四分位數:Q1,Q2和Q3。
Q1:第一四分位數 (Q1),又稱“較小四分位數”,等于該樣本中所有數值由小到大排列后第25%的數字。
Q2:第二四分位數 (Q2),又稱“中位數”,等于該樣本中所有數值由小到大排列后第50%的數字。
Q3:第三四分位數 (Q3),又稱“較大四分位數”,等于該樣本中所有數值由小到大排列后第75%的數字。
迷你距 也叫“四分位距”
迷你距。它是一組數據中較小四分位數與較大四分位數之差。
即:迷你距= 上四分位數 - 下四分位數
迷你距可以反映中間50%的數據,如果出現了極大或極小的異常值,將會被排除在中心數據50%以外。因此使用迷你距可以剔除數據中異常值。
全距,四分位距,箱形圖可以表征一組數據極大和極小值之間的差值跨度,一定程度上反應了數據的分散程度,但是卻無法精準的告訴我們,這些數值具體出現的頻率,那么我們該如何表征呢?
我們度量每批數據中數值的“變異”程度時,可以通過觀察每個數據與均值的距離來確定,各個數值與均值距離越小,變異性越小數據越集中,距離越大數據約分散,變異性越大。方差和標準差就是這么一對兒用于表征數據變異程度的概念。
方差
方差是度量數據分散性的一種方法,是數值與均值的距離的平方數的平均值。
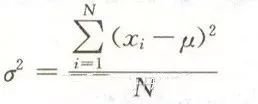
標準差
標準差為方差的開方。
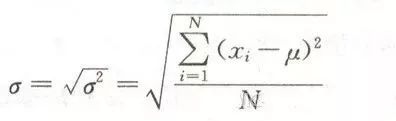
通過方差和標準差我們現在可以表征一組數據的數值的變異程度。那么對于擁有不同均值和不同標準差的多個數據集我們如何比較呢?
標準分——表征了距離均值的標準差的個數
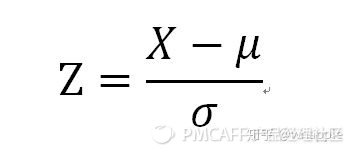
標準分為我們提供了解決方法,當比較均值和標準差各不相同的數據集時,我們可以把這些數值視為來自同一個標準的數據集,然后進行比較。標準分將把每一個數據集轉化為通用的分布形態,進行比較。
標準分還有個重要的作用,它可以把正態分布變為標準正態分布,后文會有介紹。
第一部分小結
1. 描述一批數據,通過集中趨勢分析,找出其“代表值” ;通過分散和變異性的描述,查看這批數據的分散程度。
2. 集中趨勢參數:均值,中位數,眾數
3. 分散性和變異性參數 : 全距,四分位距,方差,標準差,標準分
02
關于“事件”的研究分析
概率論
1. 一個事件的情況
為了讓讀者更好理解,筆者概率論中最核心的概念以及概念之間彼此的關系繪制成了下圖,那么接下來筆者開始“講故事”了。
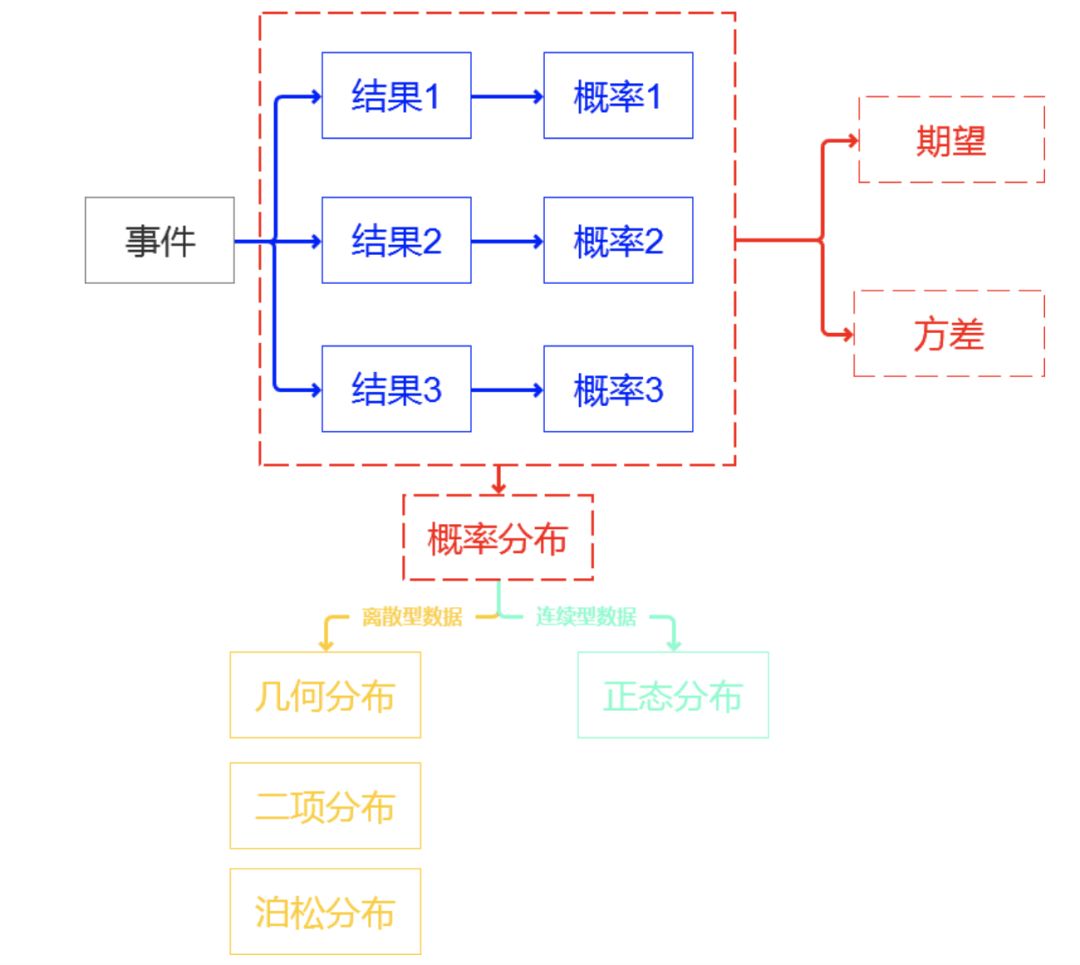
事件:有概率可言的一件事情,一個事情可能會發生很多結果,結果和結果之間要完全窮盡,相互獨立。
概率:每一種結果發生的可能性。所有結果的可能性相加等于1,也就是必然!!!
概率分布:我們把事件和事件所對應的概率組織起來,就是這個事件的概率分布。
概率分布可以是圖象,也可以是表格。如下圖1和表2都可以算是概率分布
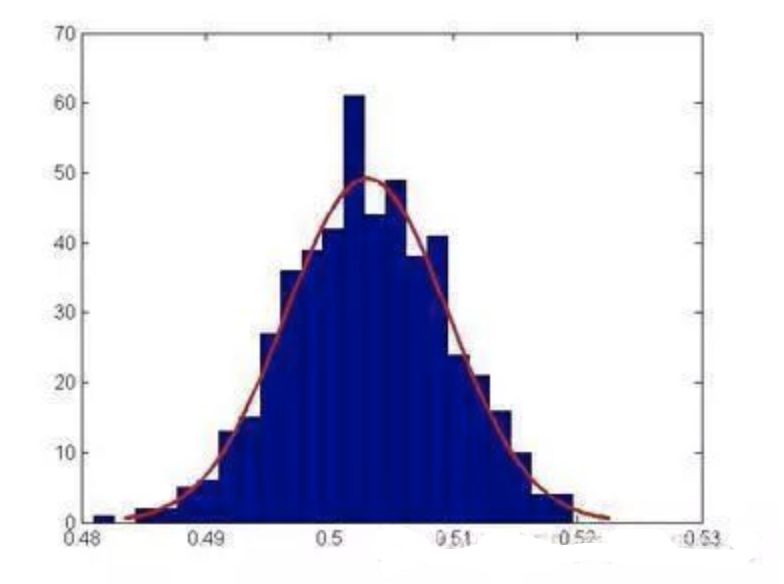

期望:表征了綜合考慮事情的各種結果和結果對應的概率后這個事情的綜合影響值。(一個事件的期望,就是代表這個事件的“代表值”,類似于統計里面的均值)
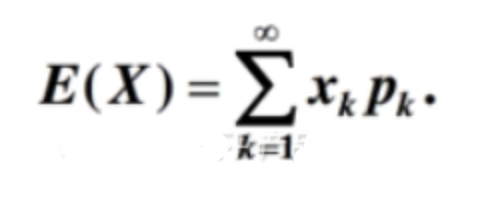
方差:表征了事件不同結果之間的差異或分散程度。
2. 細說分布
理想很豐滿,現實很骨感。真實的生活中別說去算一個事件的期望,即使把這個事件的概率分布能夠表述完整,每個事件對應的概率值得出來就已經是一件了不起的事情了。
因此,為了能更快更準確的求解出事件的概率分布,當某些事件,滿足某些特定的條件,那么我們可以直接根據這些條件,來套用一些固定的公式,來求解這些事件的分布,期望以及方差。
“離散型”數據和“連續性”數據差異
在我們展開分布的知識之前,先補充一個預備知識,什么是離散數據,什么是連續數據,它們二者之間有什么差異?
離散數據: 一個粒兒,一個粒兒的數據就是離散型數據。
連續數據: 一個串兒,一個串兒的數據就是連續型數據。
好啦,開個玩笑!!!別打我,下面分享干貨!!!
其實上述描述并沒有錯誤,離散型和連續型數據是一對相對概念,同樣的數據既可能是離散型數據,又可能是連續型數據。判別一個數據是連續還是離散最本質的因素在于,一個數據組中數據總體的量級和數據粒度之間的差異。差異越大越趨近于連續型數據,差異越小越趨近于離散型數據。
舉個例子:
人這個單位,對于一個家庭來說,就離散型數據,一個家庭可能有 3個人,4個人,5個人。..。等等。
對于一個國家來說,就是連續型數據,我們的國家有14億人口,那么以個人為單位在這個量級的數據群體里就是連續型數據。
清楚了離散型和連續型數據的差異,我們接下來一塊科普這幾種常用的特殊分布。
離散型分布
離散數據的概率分布,就是離散分布。這三類離散型的分布,在“0-1事件”中可以采用,就是一個事只有成功和失敗兩種狀態。

連續型分布
連續型分布本質上就是求連續的一個數據段概率分布。
正態分布
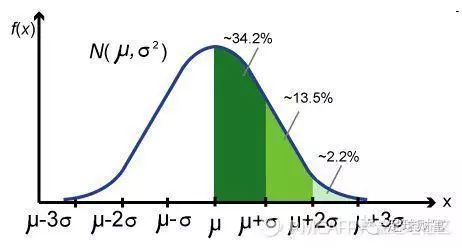
f(x)----是該關于事件X的概率密度函數
μ --- 均值
σ^2 ---方差
σ ---標準差
綠色區域的面積 ---該區間段的概率
正態分布概率的求法
step1 --- 確定分布和范圍 ,求出均值和方差
step2 --- 利用標準分將正態分布轉化為標準正態分布 (還記得 第一部分的標準分嗎?)
step3 ---查表找概率
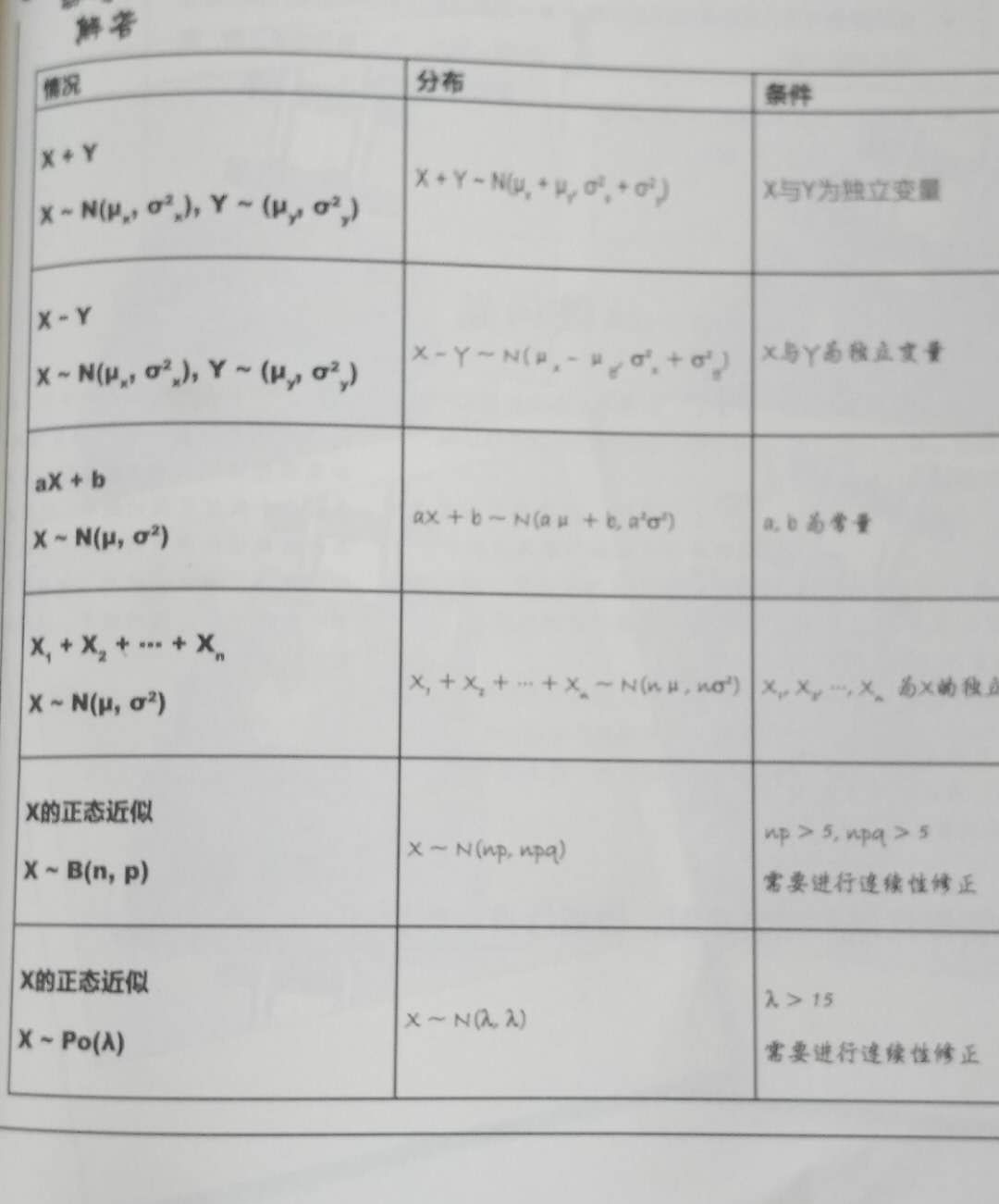
離散型分布 → 正態分布 (離散分布轉化為正態分布)
精彩的地方在這里,筆者已經闡述了連續型數據和離散型數據是一對相對的概念,那么這就意味著在某種“邊界”條件下,離散型分布和連續型分布之間是可以相互轉化的。進而簡化概率分布的計算。這里筆者不在偷懶直接上皂片了(編公式快吐了!!!!)
3. 多個事件的情況:“概率樹”和“貝葉斯定理”
多個事件就要探討事件和事件之間的關系
對立事件:如果一個事件,A’包含所有A不包含的可能性,那么我們稱A’和A是互為對立事件
窮盡事件:如何A和B為窮盡事件,那么A和B的并集為1
互斥事件:如何A和B為互斥事件,那么A和B沒有任何交集
獨立事件:如果A件事的結果不會影響B事件結果的概率分布那么A和B互為獨立事件。
例子:10個球,我隨機抽一個,放回去還是10個球,第二次隨機抽,還是10選1,那么第一次和第二次抽球的事件就是獨立的。
相關事件:如果A件事的結果會影響B事件結果的概率分布那么A和B互為獨立事件。
例子:10個球,我隨機抽一個,不放回去還是10個球,第二次隨機抽是9選1,那么第一次和第二次抽球的事件就是相關的。
條件概率(條件概率,概率樹,貝葉斯公式)
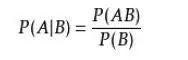
條件概率代表:已知B事件發生的條件下,A事件發生的概率
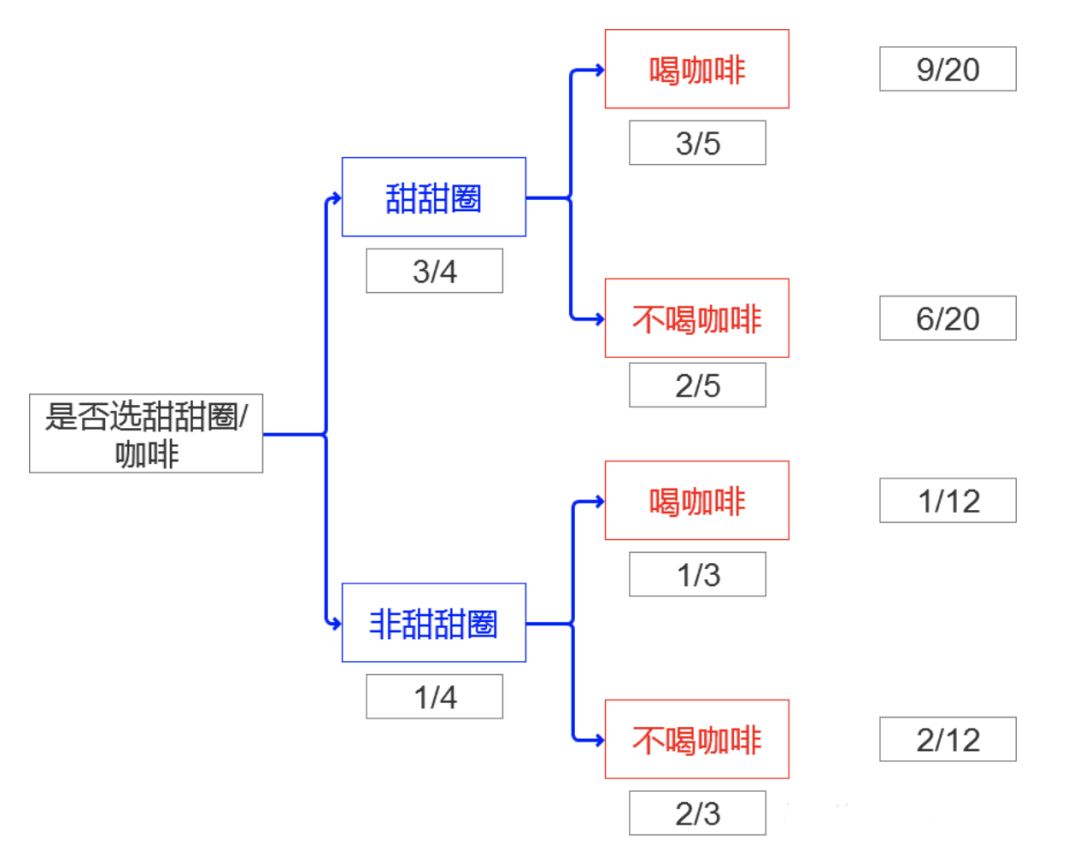
概率樹 --- 一種描述條件概率的圖形工具。
假設有個甜品店,顧客買甜甜圈的概率是3/4 ;不買甜甜圈直接買咖啡的概率是1/3 ;同時買咖啡和甜甜圈概率是9/20。
從圖中我們可以發現以下兩個信息:
1. 顧客買不買甜甜圈可以影響喝不喝咖啡的概率,所以事件甜甜圈與事件咖啡是一組相關事件
2. 概率樹每個層級分支的概率和都是1
貝葉斯公式 ----提供了一種計算逆條件概率的方法
貝葉斯公式用于以下場景,當我們知道A發生的前提下B發生的概率,我們可以用貝葉斯公式來推算出B發生條件下A發生的概率。
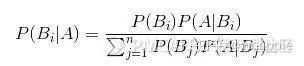
第二部分小結
1. 事件,概率,概率分布之間的關系
2. 期望,方差的意義
3. 連續型數據和離散型數據之間的區別和聯系
4. 幾何分布,二項分布,泊松分布,正態分布,標準正態分布
5. 離散分布和正態分布可以轉化
6. 多個事件之間的關系,相關事件和獨立事件,條件概率和貝葉斯公式
03
關于“小樣本”預測
“大總體”
現實生活中,總體的數量如果過于龐大我們無法獲取總體中每個數據的數值,進行對總體的特征提取進而完成分析工作。那么接下來就用到了本章節的知識。

1. 抽取樣本
總體:你研究的所有事件的集合
樣本:總體中選取相對較小的集合,用于做出關于總體本身的結論
偏倚:樣本不能代表目標總體,說明該樣本存在偏倚
簡單隨機抽樣: 隨機抽取單位形成樣本。
分成抽樣: 總體分成幾組或者幾層,對每一層執行簡單隨機抽樣
系統抽樣:選取一個參數K,每到第K個抽樣單位,抽樣一次。
2. 預測總體(點估計預測,區間估計預測)
點估計量--- 一個總參數的點估計量就是可用于估計總體參數數值的某個函數或算式。
場景1: 樣本無偏的情況下,已知樣本,預測總體的均值,方差。
(1) 樣本的均值 = 總體的估算均值(總體均值的點估計量) ≈ 總體實際均值(誤差是否可接受)

(2)總體方差 估計總體方差
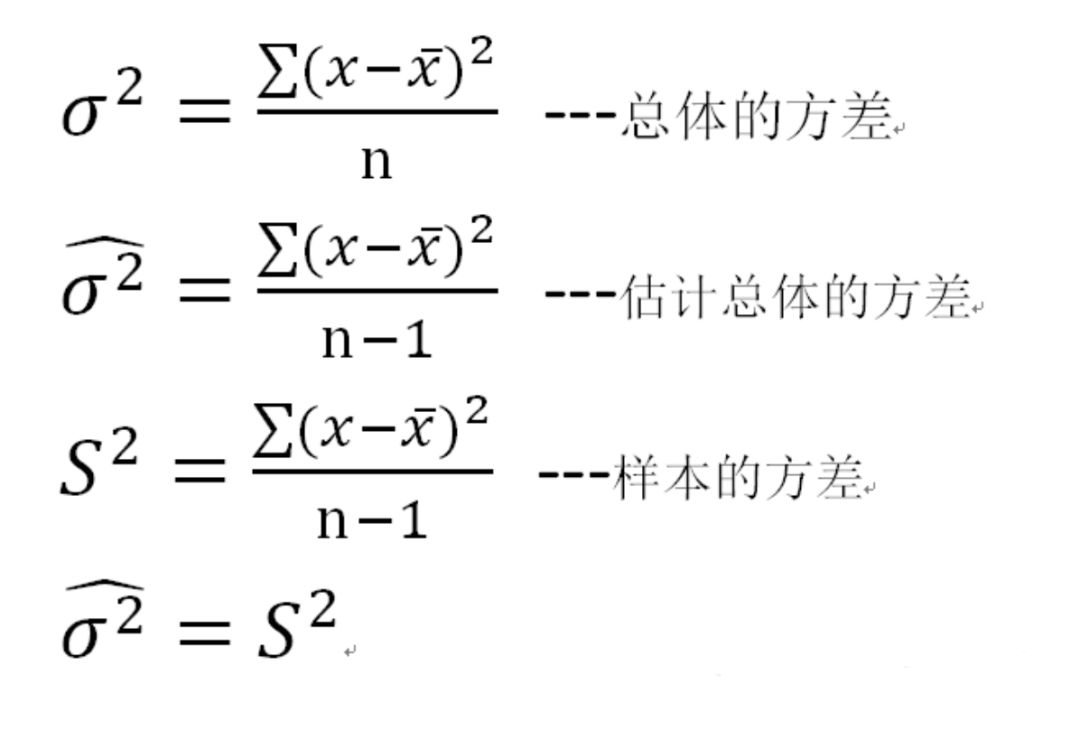
場景2:已知總體,研究抽取樣本的概率分布
比例抽樣分布:考慮從同一個總體中取得所有大小為n的可能樣本,由這些樣本的比例形成一個分布,這就是“比例抽樣分布”。樣本的比例就是隨機變量。
舉個栗子:已知所有的糖球(總體)中紅色糖球比例為0.25。從總體中隨機抽n個糖球,我們可以求用比例抽樣分布求出這n個糖球中對應紅球各種可能比例的概率。

樣本均值分布:考慮同一個總體中所有大小為n的可能樣本,然后用這個樣本的均值形成分布,該分布就是“樣本均值分布” ,樣本的均值就是隨機變量。
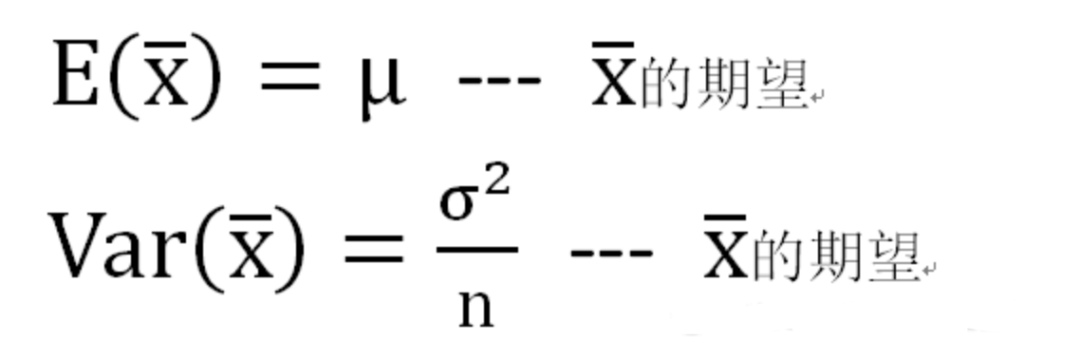
中心極限定理:如果從一個非正態總體X中抽出一個樣本,且樣本極大(至少大于30),則圖片.png的分布近似正態分布。
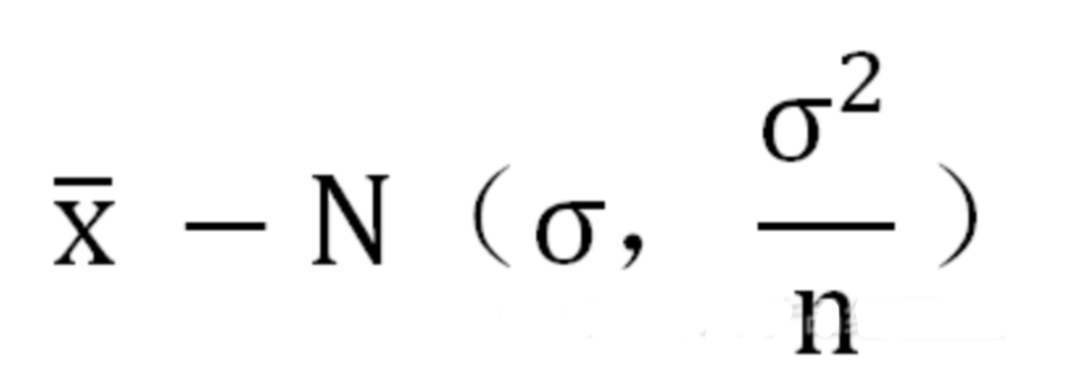
區間估計量--- 點估計量是利用一個樣本對總體進行估計,區間估計是利用樣本組成的一段區間對樣本進行估計。
舉個栗子:今天下午3點下雨;今天下午3點到4點下雨。如果我們的目的是為了盡可能預測正確,你會使用那句話術?
如何求置信區間?(這里筆者講一下思路,不畫圖碼公式了,讀者有興趣可以查閱一下教材)

求置信區間簡便公式(直接上皂片)
關于C值參數:置信水平 90% C=1.64 , 95% C=1.96 , 99% C=2.58

待補充知識一(t分布)
我們之前的區間預測有個前提,就是利用了中心極限定理,當樣本量足夠大的時候(通常大于30),均值抽樣分布近似于正態分布。若樣本量不夠大呢?這是同樣的思路,只是樣本均值分布將近似于另一種分布處理更加準確,那就是t分布。這里筆者直接放張圖,不做拓展了。

待補充知識二(卡方分布)----注意待補充不代表不重要,是筆者水平有限,目前還不能用簡單的語言概述其中的精髓。
卡方分布的定義
若n個相互獨立的隨機變量ξ、ξ、……、ξn ,均服從標準正態分布,則這n個服從標準正態分布的隨機變量的平方和構成一新的隨機變量,其分布規律稱為卡方分布。
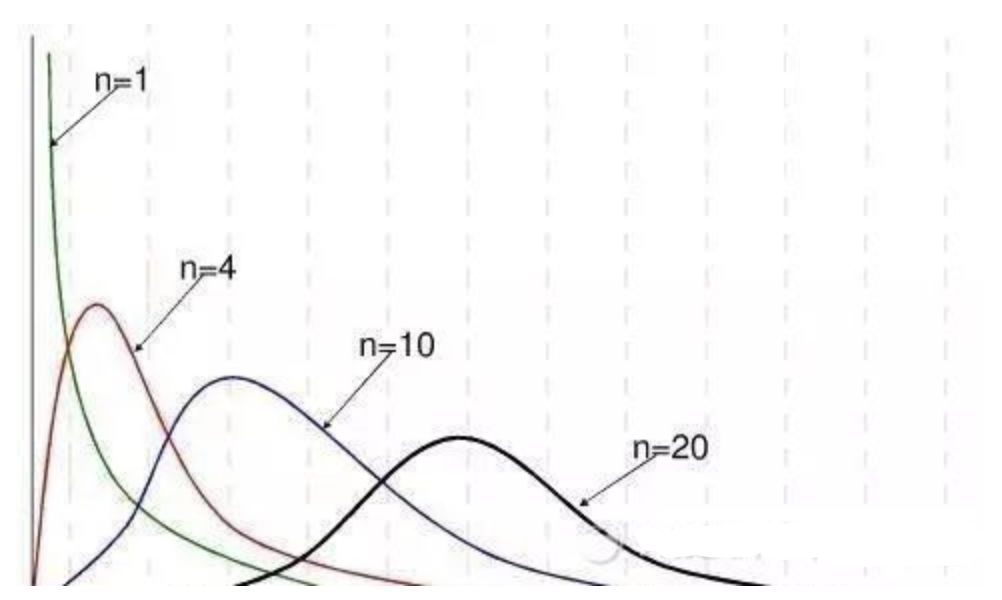
卡方分布的應用場景
用途1:用于檢驗擬合優度。也就是檢驗一組給定的數據與指定分布的吻合程度;
用途2:檢驗兩個變量的獨立性。通過卡方分布可以檢查變量之間是否存在某種關聯:
3. 驗證結果(假設檢驗)
假設檢驗是一種方法用于驗證結果是否真實可靠。具體操作分為六個步驟。

兩類錯誤---即使我們進行了“假設檢驗”依然無法保證決策是百分百正確的,會出現兩類錯誤
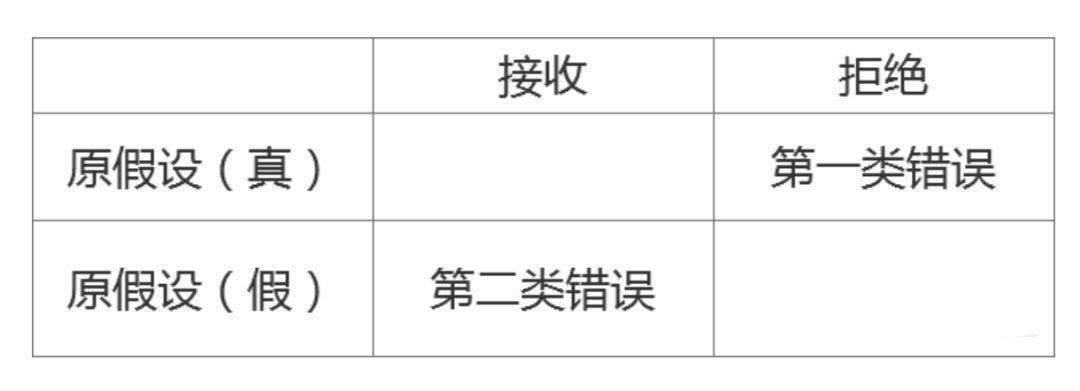
第一類錯誤: 拒絕了一個正確的假設,錯殺了一個好人
第二類錯誤:接收了一個錯誤的假設,放過了一個壞人
第三部分小結:
1. 無偏抽樣
2. 點估計量預測(已知樣本預測總體,已知總體預測樣本)
3. 區間估計量預測(求置信區間)
4. 假設檢驗
04
相關與回歸(y=ax+b)
這里介紹的相關和回歸是關于二維雙變量的最簡單最實用的線性回歸,非線性回歸這里不暫不做拓展。
散點圖:顯示出二變量數據的模式
相關性:變量之間的數學關系。
線性相關性:兩個變量之間呈現的直線相關關系。
最佳擬合直線:與數據點擬合程度最高的線。(即每個因變量的值與實際值的誤差平方和最小)
誤差平方和SSE:
線性回歸法:求最佳擬合直線的方法(y=ax+b),就是求參數a和b
斜率a公式:
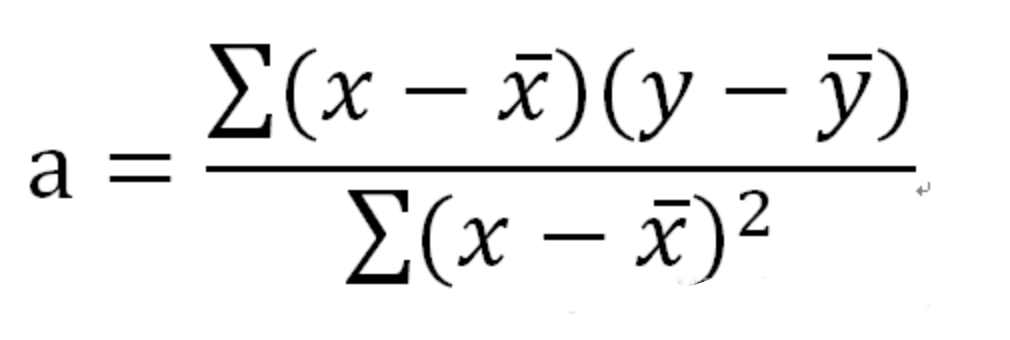
b公式:
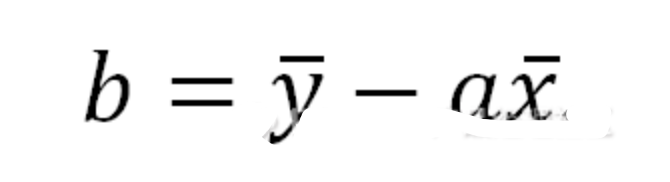
相關系數r:表征描述的數據與最佳擬合線偏離的距離。(r=-1完全負相關,r=1完全正相關,r=0不相關)
r公式:
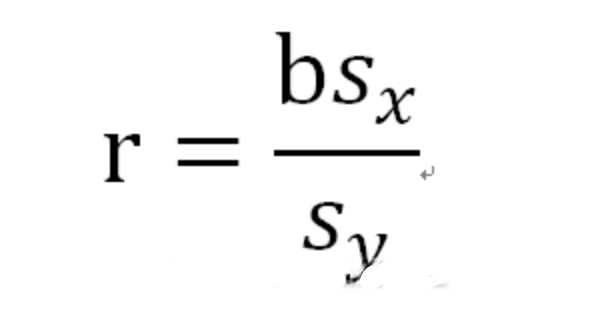
結束語
筆者這里梳理了統計與概率學最基礎的概念知識,盡量闡述清楚這些概念知識之間關聯的關系,以及應用的場景。底層概念是上層應用的基礎,當今浮躁的“機器學習”,“神經網絡”,“AI自適應”這些高大上的關鍵字滿天飛。筆者認為踏踏實實的把“基礎”打扎實,才是向上發展的唯一途徑。
-
統計
+關注
關注
1文章
19瀏覽量
13514 -
數據分析
+關注
關注
2文章
1451瀏覽量
34069
原文標題:統計學知識大梳理
文章出處:【微信號:CloudBrain-TT,微信公眾號:云腦智庫】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
一文解析半導體產業鏈條以及相關知識

一文解析半導體產業鏈條以及相關知識

什么是光子學?
示波器統計曲線和故障分析pass/fail測試
【「時間序列與機器學習」閱讀體驗】時間序列的信息提取
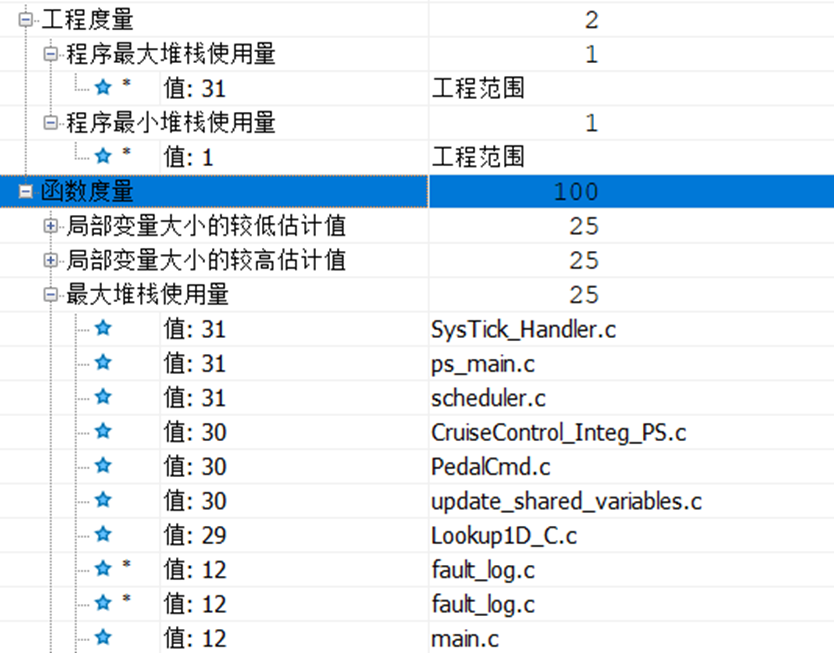
如何使用Polyspace Code Prover來統計堆棧
南京理工大學數學與統計學院師生團隊一行蒞臨中科億海微參觀交流

數據分析除了spss還有什么
自動控制原理需要哪些基礎知識
三坐標測量需要哪些基礎知識?

學鴻蒙的1萬個理由,北京中關村現大幅鴻蒙海報
降噪是什么原理 降噪方法分為哪幾種
計算攝影學基石:相機成像原理





 統計學知識大梳理
統計學知識大梳理











評論