上節(jié)我們從公式角度分析了自由空間和周期排布空間的電子的存在概率問題,那么這節(jié)我將會通過棋盤的例子幫助大家定性理解兩者之間的區(qū)別。
棋盤實驗
想象兩張棋盤,其中一張沒有格線,另一張周期性布滿格線,如下圖所示。

將電子想象為一顆棋子。這顆棋子在沒有格線約束的情況下,可以任意放在棋盤上的任何一個位置,也就是說這顆棋子出現(xiàn)在棋盤上任何位置上的概率相同。
而如果將這顆棋子放入布滿周期性格線的棋盤上,那么 這顆棋子在每個格子出現(xiàn)的概率是周期性重復(fù)的,重復(fù)的周期與格線的周期相同。 如上圖右側(cè)所示,我們假設(shè)將整個棋盤等分為5*5的格子,那么棋子在每個格子出現(xiàn)的概率為1/25,重復(fù)周期是1格。
如果棋盤沒有被等分,如下圖所示,我們假設(shè)棋子在A位置出現(xiàn)的概率為a,B位置的概率為b,那么ABCDE的概率分別為ababa,F(xiàn)之后的第二行的概率為ababa,我們發(fā)現(xiàn) 這顆棋子在每個格子出現(xiàn)的概率是周期性重復(fù)的 ,重復(fù)周期為5格。
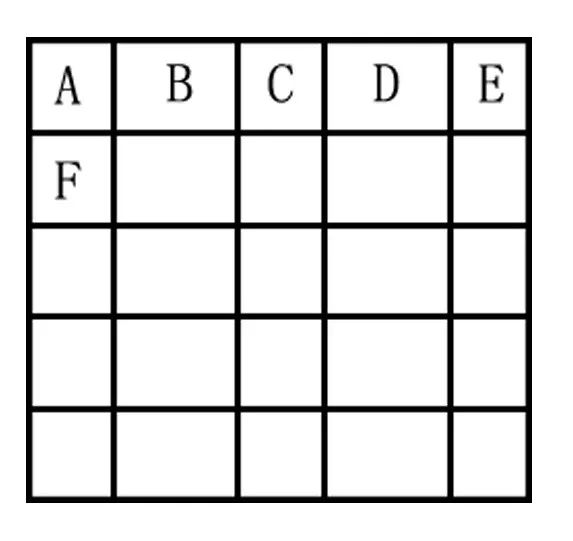
但是若選定某個格子,那么在這個格子內(nèi)部的分布則受格線的邊界條件所限制。
首先格線及附近一定距離是不能擺放棋子的,這就相當(dāng)于禁止電子存在的能級;其次,格子內(nèi)部不同位置的棋子出現(xiàn)概率,又與格子的尺寸等相關(guān),所以在單個格子內(nèi)電子出現(xiàn)概率并非處處相同。
這里描述的每一個格子其實就相當(dāng)于一個能級,而所有格子合起來就組成能帶,所有格線組合起來就組成禁帶。而格子所處的位置不同,棋子放入其中所需的能量也就不同,所以概率相同,但能量不同,即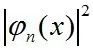 相同,但k
相同,但kn所對應(yīng)的En不同。(注:為更好地解釋自由/周期空間電子出現(xiàn)的概率問題,我們列舉了棋盤實驗,但實際情況下的能量-概率關(guān)系與棋盤實驗所得出的結(jié)論有所不同)
費(fèi)米分布
顯然任何電子的能量都是有限的,因此,有限的能級會被電子所占據(jù),那么電子在不同能級的分布概率如何呢?這里就需要引入半導(dǎo)體中非常重要的一個分布函數(shù)叫做費(fèi)米-狄拉克分布函數(shù),通常簡稱為費(fèi)米分布,即:
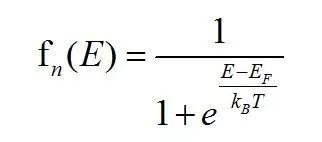

因此, 費(fèi)米能級以下的能級被電子占有的概率遠(yuǎn)遠(yuǎn)大于費(fèi)米能級以上的能級。 (擴(kuò)展:隨著溫度的上升,這個變化趨勢會變緩,也就是電子占有費(fèi)米能級以上能級的概率就會增加。)
電子的自激發(fā)和空穴的產(chǎn)生

根據(jù)泡利不相容原理,對于已經(jīng)被電子占滿的能帶就不能再有其他電子加入,因此不能導(dǎo)電;反之對于沒有被電子占滿的能帶則還可以有其他電子加入,因此可以導(dǎo)電。
半導(dǎo)體中將費(fèi)米能級以下的能帶稱為價帶,費(fèi)米能級以上的能帶稱為導(dǎo)帶。
顯然,雖然概率很低,但導(dǎo)帶底部存在一定被電子占據(jù)的概率,這就是半導(dǎo)體中自發(fā)產(chǎn)生自由電子的機(jī)制,稱為自激發(fā)。
自激發(fā)進(jìn)入導(dǎo)帶的電子,因為能帶中的絕大多數(shù)能級沒有電子,因此電子可以自由移動。而且隨著溫度的升高,自發(fā)產(chǎn)生自由電子的概率也會升高。

此外,根據(jù)電中性原理,價帶和導(dǎo)帶的電子分布具有對稱性,也就是說,導(dǎo)帶中增加多少電子,價帶中就相應(yīng)地應(yīng)該減少多少電子,物理概念上通常將這個過程描述為:由于溫度的原因,價帶的電子自發(fā) “激發(fā)” 到了導(dǎo)帶。
由于價帶中電子數(shù)量遠(yuǎn)遠(yuǎn)大于激發(fā)到導(dǎo)帶中的電子,如果價帶中的電子狀態(tài)也以每個電子為描述對象,那么過程會非常復(fù)雜。
考慮導(dǎo)帶和價帶的對稱性, 把價帶中因為電子激發(fā)而留下的空余能級想象為另一種電荷,取名叫做“空穴”。 因此,電子和空穴總是成對的產(chǎn)生,好比陽光下一個物體和他的影子,不可能獨立產(chǎn)生。
至此,我們介紹完畢電荷自發(fā)產(chǎn)生的過程,下一節(jié)我將為小伙伴們講述自發(fā)產(chǎn)生的電荷濃度問題。
文末總結(jié)
1、通過棋盤實驗理解能級、禁帶、能帶;

3、通過實際來分析費(fèi)米分布,理解價帶和導(dǎo)帶:半導(dǎo)體中將費(fèi)米能級以下的能帶稱為價帶(不能導(dǎo)電),費(fèi)米能級以上的能帶稱為導(dǎo)帶(能導(dǎo)電)。
4、得到電子/空穴產(chǎn)生的原因:由于導(dǎo)帶底部存在一定被電子占據(jù)的概率,半導(dǎo)體中會自發(fā)產(chǎn)生自由電子,該機(jī)制被稱為自激發(fā)。考慮導(dǎo)帶和價帶的對稱性,把價帶中因為電子激發(fā)而留下的空余能級想象為另一種電荷,取名叫做“空穴”。
-
半導(dǎo)體
+關(guān)注
關(guān)注
335文章
28970瀏覽量
239056 -
電荷
+關(guān)注
關(guān)注
1文章
653瀏覽量
36798
發(fā)布評論請先 登錄
TXB0104與TXS0102兩者之間有什么區(qū)別嗎?
請問TMS320F2802PZA和TMS320F2802PZA-60兩者之間的區(qū)別
單片機(jī)和嵌入式兩者有什么區(qū)別和聯(lián)系呢
怎樣去區(qū)分RK3288和RK3288W兩者之間的型號呢
有人可以告訴我keil和stm32cube ide兩者之間有什么區(qū)別嗎
PCB干膜和濕膜具體指什么?兩者之間的區(qū)別在哪里?
自由空間光交換,自由空間光交換是什么意思
建立自由空間光學(xué)系統(tǒng)
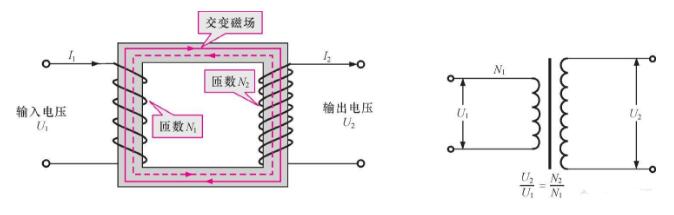
讀懂變壓器空載與負(fù)載及兩者之間的區(qū)別
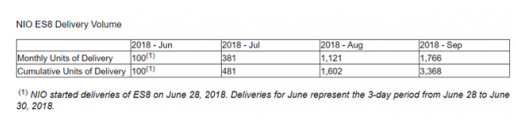
蔚來與特斯拉兩者之間的相同點和不同點淺析
淺析人工智能和機(jī)器學(xué)習(xí)兩者之間的區(qū)別
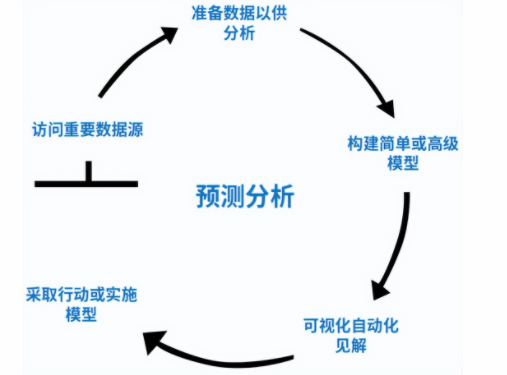
機(jī)器學(xué)習(xí)和預(yù)測分析兩者之間如何相互關(guān)聯(lián)?



















評論