 論文鏈接:https://arxiv.org/abs/2305.10299
論文鏈接:https://arxiv.org/abs/2305.10299代碼鏈接1:
https://github.com/caiyuanhao1998/BiSCI代碼鏈接2:
https://github.com/caiyuanhao1998/MST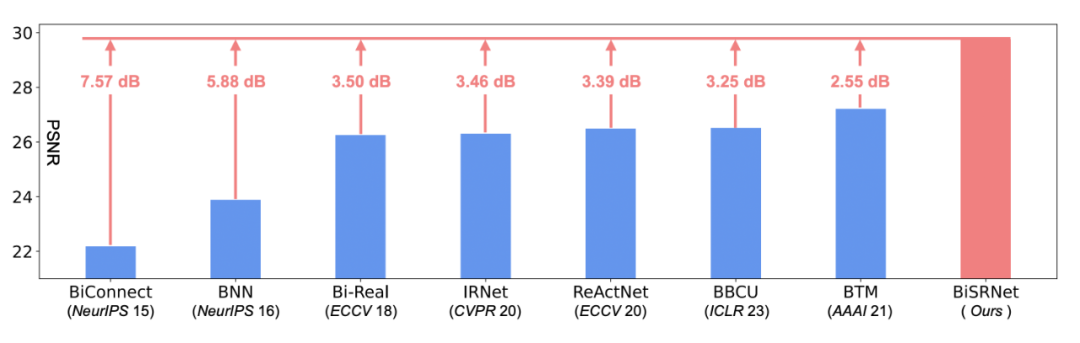
▲ 圖1 BiSRNet 與當前最先進的二值網絡的性能對比
目前所有的代碼,預訓練模型和測試結果均已開源在我們開發的一個二值化光譜壓縮重建工具包 BiSCI 內,該工具包支持八類最主要的二值網絡,歡迎大家來使用。同時,我們還將 BiSRNet 嵌入到了我們之前開發的光譜重建工具箱 MST 當中。目前 MST 工具包已支持超過 12 類深度學習算法,并包含各種配套的可視化函數,歡迎大家來對比。
 光譜壓縮重建任務介紹
光譜壓縮重建任務介紹相比于常規的三通道 RGB 圖像,高光譜圖像包含幾十上百個波段,從而捕獲了關于成像場景更豐富的信息。也正因為這一重要特性,高光譜圖像被廣泛地應用于醫療,地形勘探,農業等領域。如圖 2 所示,在醫院進行檢查時,如果只看常規的 RGB 圖像可能很難診斷病因,但是如果采用高光譜圖像捕獲并在特定波長下渲染的話,就可以看清楚各類血管,骨骼結構等,從而輔助醫生診斷。同樣的原理也可應用在遙感地形勘探和農業病蟲害檢測。
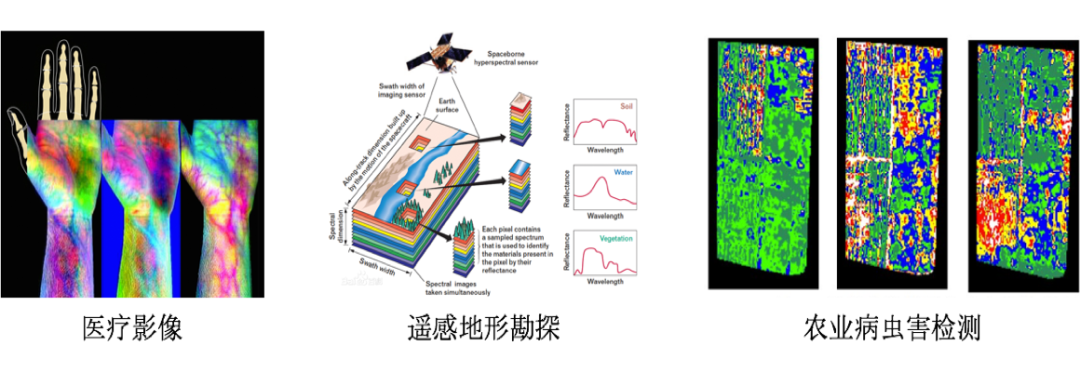
▲圖2 高光譜圖像的應用
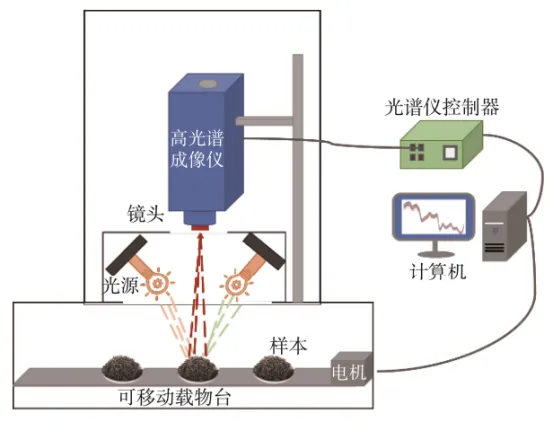
然而高光譜圖像并容易獲取,傳統的成像設備采用光譜儀對成像場景進行逐波段的掃描,費時費力,難以捕捉運動場景。近些年,科學家們專門設計了單曝光壓縮成像(Snapshot Compressive Imaging,SCI)系統來解決這一問題。其光路結構如圖 3 所示。
該系統首先通過一個編碼孔徑掩膜對成像場景的各光譜通道進行調制,然后通過一個三棱鏡進行色散后在相機上捕獲到一個二維的快照估計圖(compressive measurement)。通過這個光路系統,我們便可將三維的光譜立方塊壓縮成一個二維的圖像。而光譜壓縮重建的任務便是從這個二維的壓縮估計圖上恢復出三維的高光譜數據。
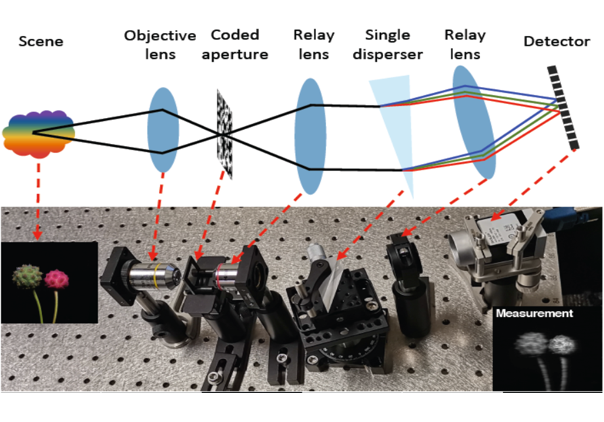
▲圖3 單曝光壓縮成像系統
當前的主流方法是采用的是全精度模型如 CNN 或者 Transformer 來學一個從壓縮估計圖到三維光譜立方塊的映射。幾個比較經典算法有我們之前的工作 MST,MST++,CST,DAUHST,HDNet 等(這些方法全部都開源在我們的工具箱 MST 當中)。
這類方法雖然取得了很好的重建效果,但卻難以部署到移動端設備(如智能手機、相機、無人機等)上,因為移動端設備的內存空間,計算資源和電力均有限,無法運轉全精度模型。另一方面,全精度模型的一些計算單元如深度展開算子和多頭自注意力機制等相對復雜,移動端設備無法支持。為了推動光譜重建算法的實際應用,本文做了如下貢獻:
(1)提出了光譜壓縮重建領域內首個基于二值神經網絡(Binarized Neural Network,BNN)的算法——二值化光譜重分布網絡(Binarized Spectral-Redistribution Network,BiSRNet)。
(2)設計了一個新的二值化卷積單元——二值化光譜重分布卷積(Binarized Spectral-Redistribution Convolution,BiSR-Conv)。該卷積單元可以調整光譜表征的強度和分布,同時在反向傳播中更好地逼近二值化符號(Sign)函數,從而讓求得的梯度更加準確。
(3)制作了四個二值化卷積模塊來解決特征圖形變過程中的維度不匹配問題,從而讓全精度信息能流通整個模型的每一層卷積單元以彌補二值卷積造成的信息損失。
(4)我們的 BiSRNet 顯著地超越了當前最先進的二值化算法,甚至取得了能與全精度 CNN 比肩的效果,然而我們的 BiSRNet 算法卻只需要極低的存儲空間(約 0.06 %)和計算代價(約 1 %)。

本文方法
2.1 基礎模型
一般來說,用于二值化的全精度模型應該是比較輕量的且它的計算單元可以再移動端設備上運行。然而,現存的 CNN 或 Transformer 模型均不滿足這一要求。為此,我們重新設計了一個簡單,輕量,易于部署的基礎模型(Base Model)。
受到之前工作 MST,MST++,CST,DAUHST 的啟發,我們設計的基礎模型也采用一個 U 形結構,如圖 4 所示。
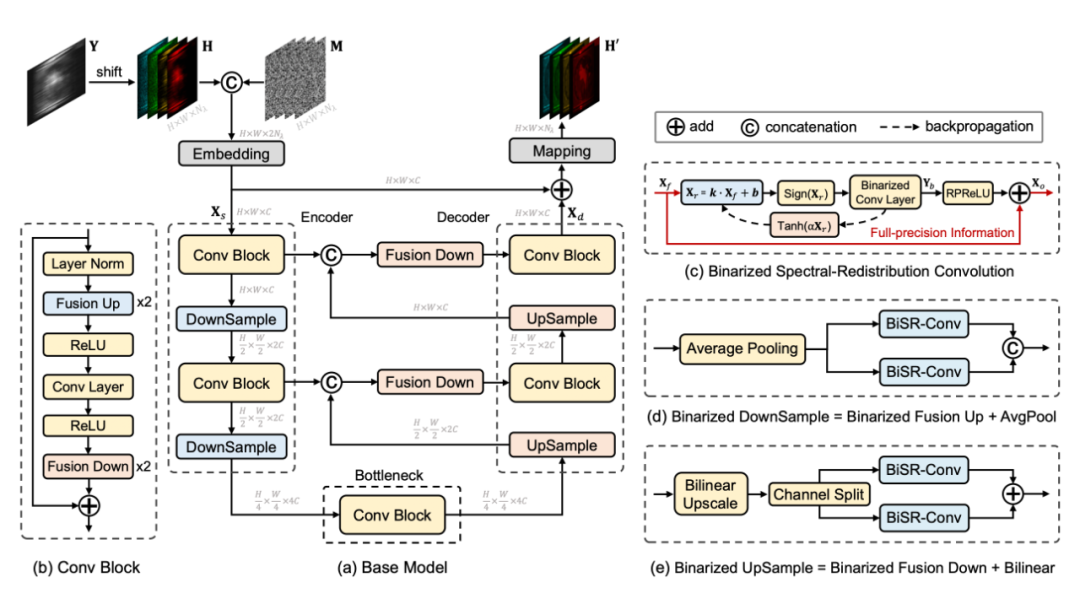
▲圖4 基礎模型的網絡結構
在這個基礎模型中,采用的所有計算單元都可以被移動端設備支持,同時也不涉及計算復雜度高的操作。
2.2 二值化光譜重分布卷積單元
二值化光譜重分布卷積的細節如圖 4(c)所示。將輸入的全精度激活信號記為 。我們注意到,受到特定成像波長的限制,高光譜信號沿著光譜維度有著不同的強度與分布。為了適應光譜圖像的這一特性,我們提議在二值化激活之前,按通道對高光譜圖像表示進行重分布:
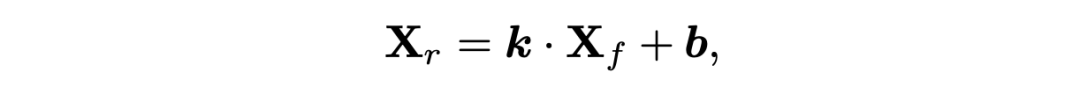
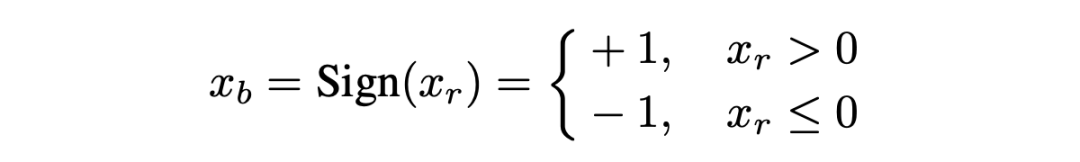
如圖 5(b)和(c)所示,由于符號函數是不可導的,之前的方法大都采用一個分段線性函數 Clip(x)或者二次函數 Quad(x)來在反向傳播中擬合符號函數。
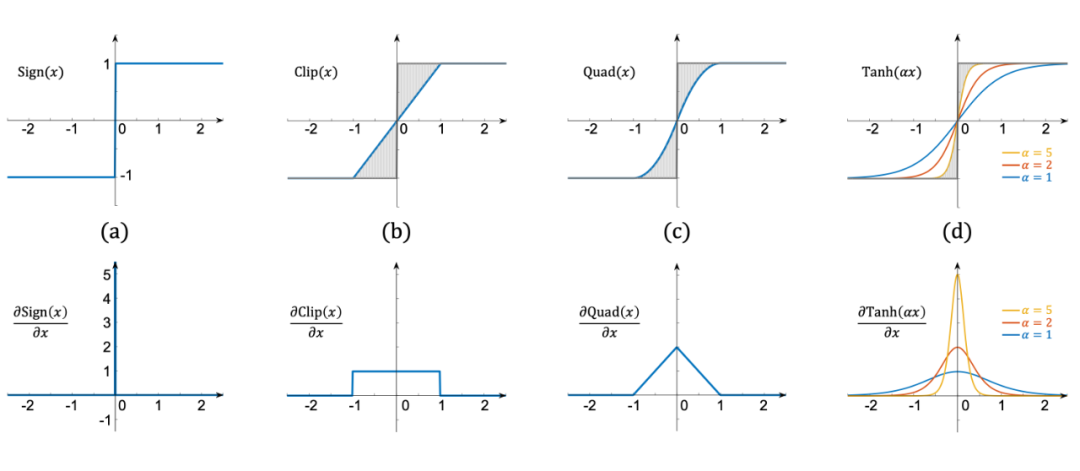
▲圖 5 符號函數與各類逼近函數的對比圖
Clip(x)與 Quad(x)的具體表達式如下:
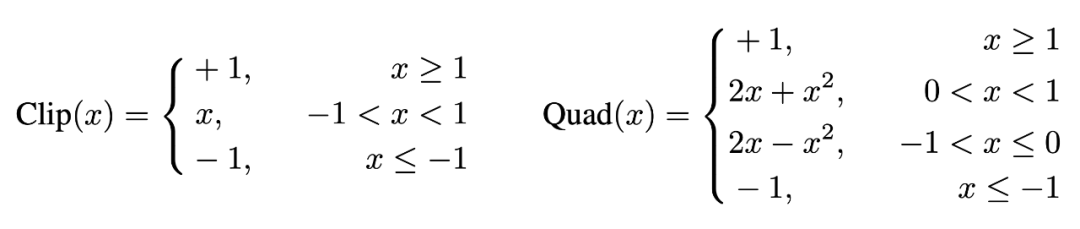
然而分段線性函數知識一個粗略的估計,它與符號函數之間依舊有著很大的誤差。圖 5 中的陰影部分面積就表示這個誤差的大小,Clip(x)的誤差是 1。此外,一旦激活或者權重的值落在了 [-1,1] 之外,他們就不會再被更新。盡管分段二次函數是一個更精確的逼近(誤差為 2/3),上述的兩個問題依舊存在。為此,我們設計了一個可縮放的雙曲正切函數來在反向傳播中擬合符號函數:
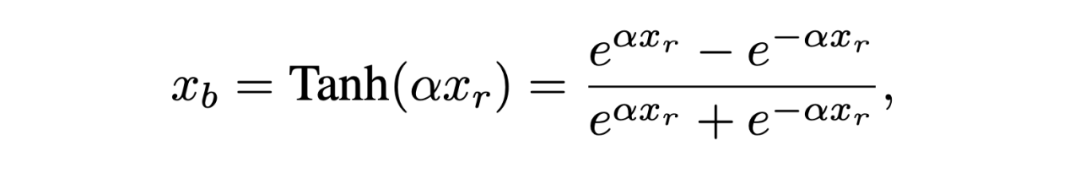
其中 是一個可學習的參數,自適應地調整 Tanh()與 Sign()之間的距離。我們證明當 時,Tanh()→ Sign()如下:
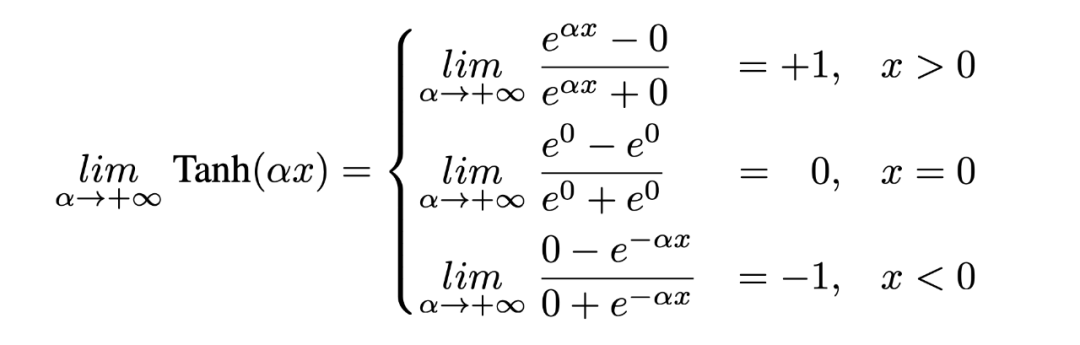
我們仿照之前的二值化算法,定義:。然后我們可以得到:
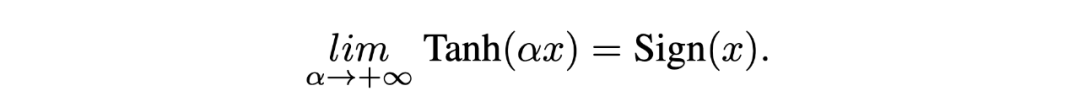
我們計算圖 5(d)中的陰影面積:
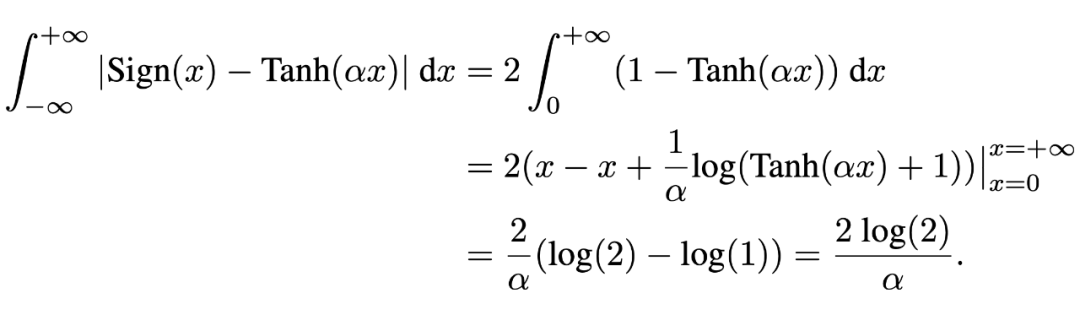
由此可見,當 足夠大時,Tanh()可以任意地逼近 Sign()。同時,我們的 Tanh()既不是分段函數,也不會因為 x 落在 [-1,1] 之外而無法更新。
更進一步,我們比較三個逼近函數的一階導數。如圖 5 下邊一行所示,與的取值范圍均為 ,這與有著本質的區別。而我們的可以通過改變參數 來調整它的取值范圍 和形狀,從而更加靈活地逼近。
在二值化卷積層當中,32 位的權重 也被二值化到一位的權重 :
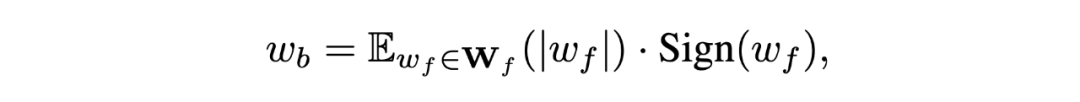
其中的 表示取均值。由此,計算繁重的全精度卷積操作便可由純邏輯異或非運算(XNOR)與位計數(bit-count)操作替換如下:
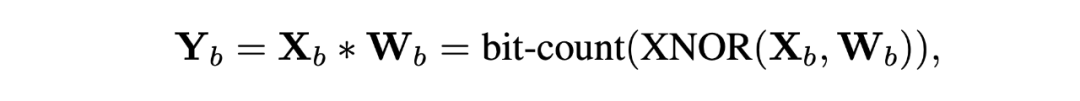
因為全精度信息 的取值范圍與二值卷積的輸出 差別較大,直接引入殘差連接將兩者相加容易導致 的信息被淹沒掉,所以先采用一個 RPReLU 激活函數來重塑 的取值范圍:
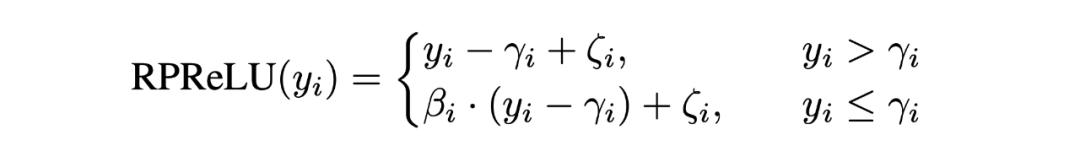
然后再引入殘差鏈接:
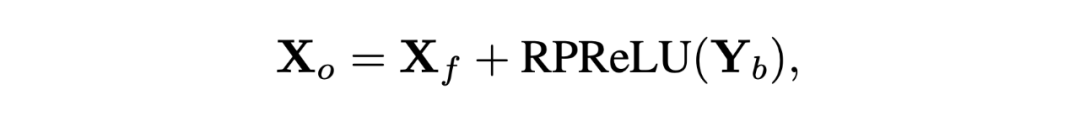
通過我們的設計,全精度信息流就不會被二值卷積給阻斷,從而能夠順暢地流過我們設計的 BiSR-Conv 單元,如圖 4 (c) 中的紅色箭頭所示。
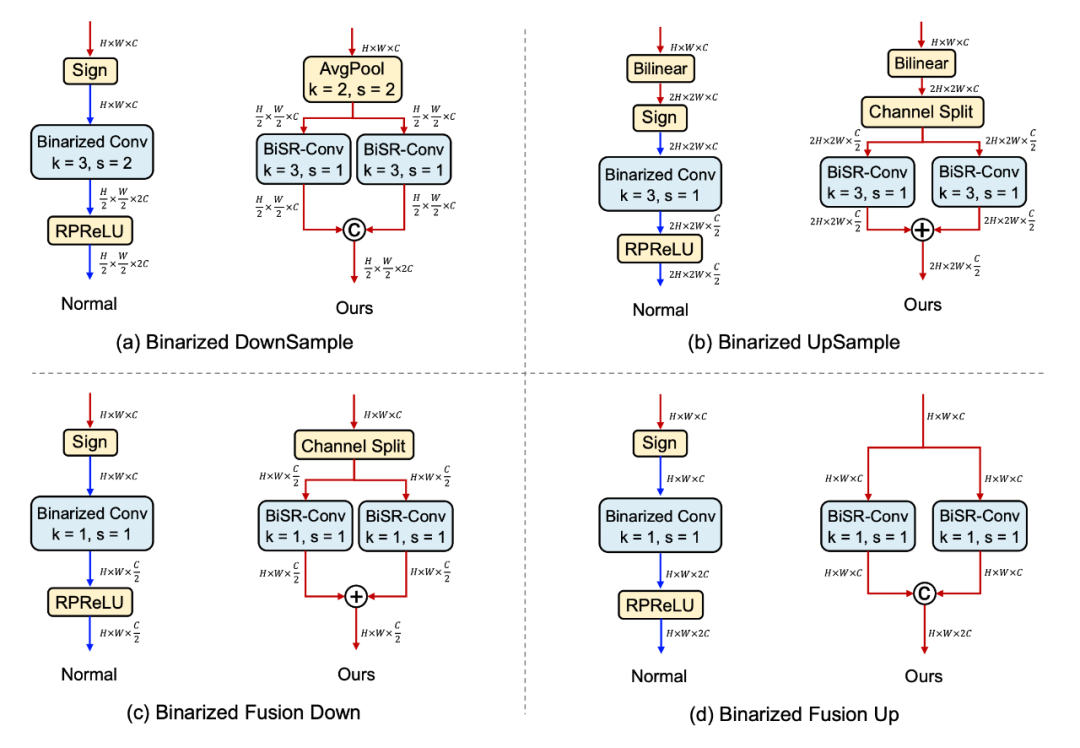
全精度信息流在二值化算法中非常重要,因為它在一定程度上彌補了量化導致的信息損失。然而在特征圖的上下采樣過程中,由于維度發生了變化,難以直接引入殘差鏈接以補充全精度信息,如圖 6 中每個子圖的左半部分所示。藍色箭頭表示二值信號,紅色箭頭表示全精度信息流。普通的二值卷積模塊會在特征度維度改變的同時阻斷全精度信息流的傳遞。然而我們的二值卷積模塊通過采用分割合并的技巧,讓全精度信息流不被阻斷,從而在整個二值模型中流通。

實驗結果
3.1 量化指標
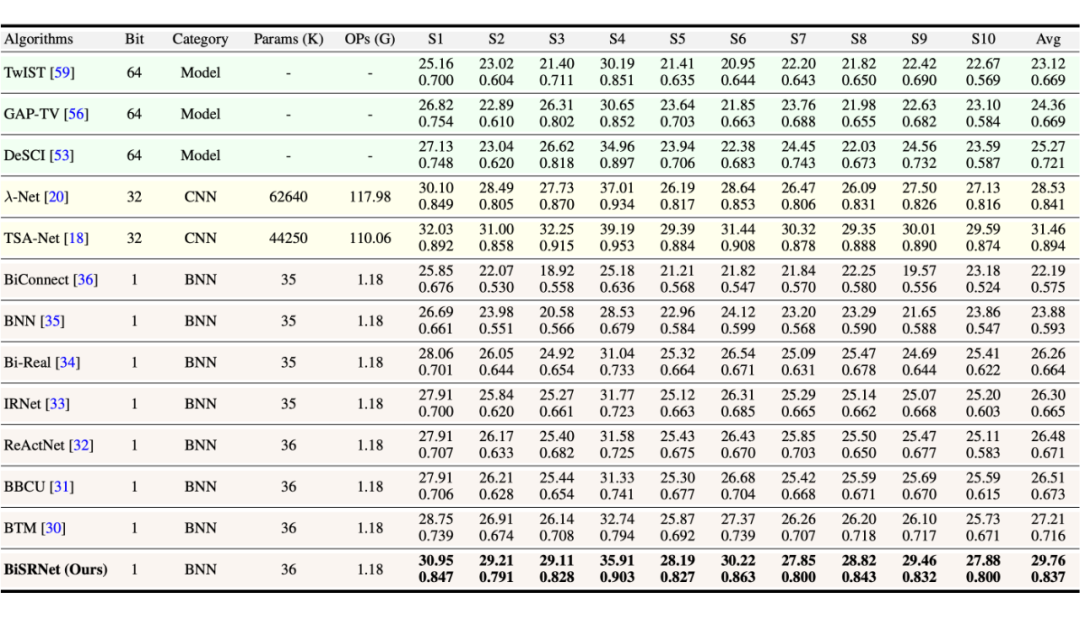
3.2 視覺對比
 ▲圖7 BiSRNet 與其他 BNN 方法在仿真數據及上的視覺對比
▲圖7 BiSRNet 與其他 BNN 方法在仿真數據及上的視覺對比 ▲??圖8 BiSRNet 與其他 BNN 方法在真實數據集上的視覺對比
▲??圖8 BiSRNet 與其他 BNN 方法在真實數據集上的視覺對比
總結
本文首次探索了壓縮量化在光譜壓縮重建領域的應用,提出了該領域首個二值化卷積神經網絡 BiSRNet,在量化指標和視覺結果上都顯著地超越了當前最先進的二值化模型。代碼,預訓練權重,重建結果均開源在:https://github.com/caiyuanhao1998/BiSCI ·
-
物聯網
+關注
關注
2909文章
44736瀏覽量
374484
原文標題:NeurIPS 2023 | 清華ETH提出首個二值化光譜重建算法
文章出處:【微信號:tyutcsplab,微信公眾號:智能感知與物聯網技術研究所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
Teledyne Lecroy示波器插值算法
一種基于深度學習的二維拉曼光譜算法

愛芯元智受邀參加2024清華自動化論壇
基于高光譜成像的法醫痕跡非接觸分析
什么是光纖光譜儀?光纖光譜儀的應用
阿里云推出首個域名AI大模型應用
CO2 AI推出首個大規模產品排放量計算解決方案

康謀分享 | aiSim5仿真場景重建感知置信度評估(三)





 NeurIPS 2023 | 清華ETH提出首個二值化光譜重建算法
NeurIPS 2023 | 清華ETH提出首個二值化光譜重建算法
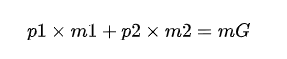










評論