布斯算法介紹
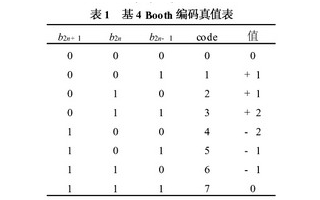
Booth 的算法檢查有符號二的補碼表示中 'N'位乘數 Y 的相鄰位對,包括低于最低有效位 y?1 = 0 的隱式位。對于每個位 yi,對于從 0 到 N ? 1 的 i,考慮位 yi 和 yi?1。當這兩個位相等時,乘積累加器P保持不變。其中 yi = 0 且 yi?1 = 1,乘以 2i 添加到 P;其中 yi = 1 且 yi?1 = 0,則從 P 中減去乘以 2i。P 的最終值為有符號結果。
未指定乘數和乘積的表示形式;通常,這些也都在二的補碼表示中,就像乘數一樣,但是任何支持加法和減法的數字系統也可以工作。如此處所述,步驟的順序尚未確定。通常,它從LSB到MSB,從i = 0開始;然后乘以2i通常被P累加器在步長之間向右的增量移位所取代;低位可以移出,然后可以在P的最高N位上進行后續的加法和減法。
該算法通常被描述為將乘數中 1 的字符串轉換為字符串末端的高階 +1 和低階 ?1。當字符串通過 MSB 運行時,沒有高階 +1,并且凈效應被解釋為相應值的負數。
計算步驟
使用的寄存器:A,M,Q,Qres(Qres是Q右移后的殘余位),n(計數器)
第1步: 加載寄存器的初始值。
A = 0(累加器),Qres = 0,M = 乘法,Q = 乘法器,n是等于乘法器位數的計數值。
第2步: 檢查 {Q0,Qres} 的值。如果為 00 或 11,請轉到步驟 5。如果為01,轉到步驟3。如果為 10,轉到步驟 4。
第3步: 執行 A = A + M,轉到步驟 5。
第4步: 執行 A = A - M。
第5步: 執行 {A,Q,Qres} 的算術位移和遞減計數。
第6步: 檢查計數器值 n 是否為零。如果是,請轉到下一步。否則轉到步驟 2。
第7步: 停止計算,輸出計算結果。
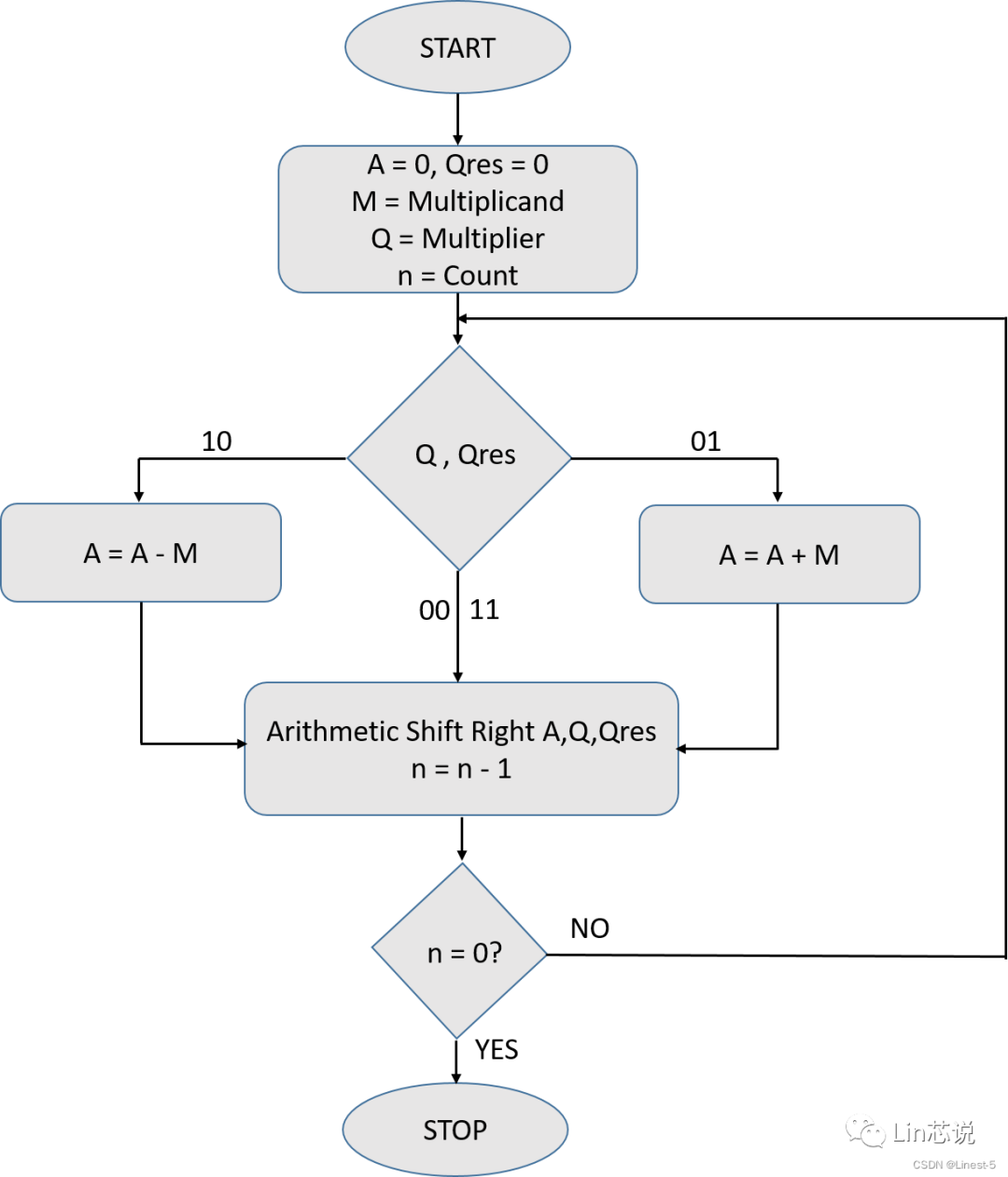
計算流程圖
以下是布斯計算的流程圖,從圖中可以清楚的看出計算的過程,簡單的來說就是判定乘數的最低位和次低位,如果兩位相同則直接執行移位操作,如果兩者不同,如為“10”則將原始值減去被乘數,如為“01”則將原始值加上被乘數。
舉個栗子
下面就以被乘數為6,乘數為-4為例,做一個計算過程的舉例。
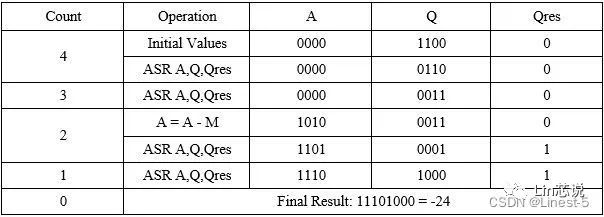
- 將所有寄存器初始化,累加器A初始化為0,乘數加載寄存,最低位移出位設定為0。
- 判定最低位和移出位為“00”,不進行加減操作,將結果結果值右移一位。
- 判定最低位和移出位為“00”,不進行加減操作,將結果結果值右移一位。
- 判定最低位和移出位為“10”,對累加器減去被乘數,并將結果結果值右移一位,注意此時累加器A為負數。
- 判定最低位和移出位為“10”,不進行加減操作,將結果結果值右移一位,此時累加器為負數,因此右移最高位補1。
- 判定最低位和移出位為“10”,不進行加減操作,將結果結果值右移一位,此時累加器為負數,因此右移最高位補1。
- 計數器為0表示計算完成,停止計算并輸出計算結果值。
Verilog 實現
設計思想
總的來說和上面提到的計算步驟是一致的,利用三段狀態機實現,分別為空閑狀態、計算狀態和完成狀態,其中空閑狀態等待開始計算信號的到來,計算狀態完成布斯計算步驟,完成狀態輸出結果數據以及同步的有效標志信號。
Verilog 代碼
/*~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~*/
/*~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~*/
/*Engineer : Linest-5
/*File : booth_multiple.v
/*Create : 2022-08-27 16:40:34
/*Revise : 2022-08-27 16:40:34
/*Module Name : booth_multiple
/*Description : 基于布斯算法的乘法器設計
/*Editor : sublime text3, tab size (4)
/*~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~*/
/*~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~*/
modulebooth_multiple(
inputclk,
inputrst,
inputstart,
inputsigned [3:0] X,
inputsigned [3:0] Y,
outputreg signed [7:0] Z,
outputvalid
);
/*~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~*/
/*參數和信號申明 */
/*~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~*/
parameterIDLE = 3'b001;
parameterCACULATE = 3'b010;
parameterFINISH = 3'b100;
reg[2:0] state;
reg[2:0] next_state;
reg[1:0] q_reg; //右移最后兩位寄存
reg[2:0] cnt; //右移次數計數信號
/*~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~*/
/*三段狀態機 */
/*~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~*/
//狀態機第一段,狀態初始化,時序邏輯非阻塞賦值
always @(posedge clk or posedge rst) begin
if (rst) begin
state <= IDLE;
end
else begin
state <= next_state;
end
end
//狀態機第二段,狀態跳轉,組合邏輯阻塞賦值
always @(*) begin
next_state = state;
case(state)
IDLE: begin
if (start) begin
next_state = CACULATE;
end
else begin
next_state = IDLE;
end
end
CACULATE: begin
if (cnt == 'd3) begin
next_state = FINISH;
end
else begin
next_state = CACULATE;
end
end
FINISH: begin
next_state = IDLE;
end
endcase
end
//狀態機第三段,結果輸出,時序邏輯非阻塞賦值
always @(posedge clk or posedge rst) begin
if (rst) begin
cnt <= 'd0;
q_reg <= 'd0;
Z <= 'd0;
end
else begin
case(state)
IDLE: begin
cnt <= 'd0;
q_reg <= {Y[cnt],1'b0};
Z <= {4'b0000,Y};
end
CACULATE: begin
cnt <= cnt + 'd1;
q_reg <= {Y[cnt+1],Y[cnt]};
case(q_reg)
2'b00,2'b11: begin
Z <= $signed(Z) >> >1;
end
2'b10: begin
Z <= $signed({Z[7:4]-X,Z[3:0]}) >> >1;
end
2'b01: begin
Z <= $signed({Z[7:4]+X,Z[3:0]}) >> >1;
end
endcase
end
FINISH: begin
cnt <= 'd0;
q_reg <= 'd0;
Z <= Z;
end
endcase
end
end
assign valid = (state==FINISH);
endmodule
TestBench 代碼
/*~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~*/
/*~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~*/
/* Engineer : Linest-5
/* File : tb_booth_multiple.v
/* Create : 2022-08-27 19:22:46
/* Revise : 2022-08-27 20:21:49
/* Module Name : tb_booth_multiple
/* Description : 基于布斯算法的乘法器仿真模塊
/* Editor : sublime text3, tab size (4)
/*~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~*/
/*~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~*/
`timescale 1ns/1ns
module tb_booth_multiple();
reg clk;
reg rst;
reg start;
reg signed [3:0] X;
reg signed [3:0] Y;
wire signed [7:0] Z;
wire valid;
initial begin
clk = 'd0;
rst = 'd1;
#20
rst = 'd0;
end
always #10 clk = ~clk;
initial begin
#20
X = 6;
Y = -4;
start = 'd0;
#50
start = 'd1;
#20
start = 'd0;
#200
X = 7;
Y = -5;
start = 'd1;
#20
start = 'd0;
#200
X = 7;
Y = 5;
start = 'd1;
#20
start = 'd0;
end
booth_multiple inst_booth_multiple (
.clk (clk),
.rst (rst),
.start (start),
.X (X),
.Y (Y),
.Z (Z),
.valid (valid)
);
endmodule
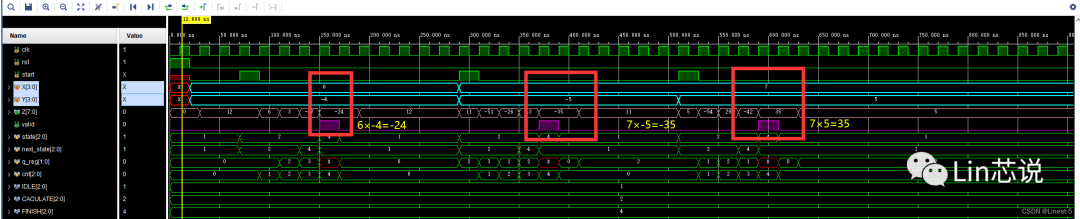
仿真波形
分別進行有符號的乘法,6和-4、7和-5、7和5,可以看到仿真波形中,正確的得到了計算結果,并且有效標志信號也同步輸出。
驗證成功!
-
寄存器
+關注
關注
31文章
5336瀏覽量
120235 -
Verilog
+關注
關注
28文章
1351瀏覽量
110077 -
乘法器
+關注
關注
8文章
205瀏覽量
37043 -
累加器
+關注
關注
0文章
50瀏覽量
9450 -
MSB
+關注
關注
0文章
13瀏覽量
8258
發布評論請先 登錄
相關推薦
基于EPF10K100EQ 240-132和Booth編碼實現位浮點陣列乘法器的設計
fpga中定點乘法器設計(中文)
怎么實現32位浮點陣列乘法器的設計?
基于跳躍式Wallace樹的低功耗32位乘法器
基于Verilog HDL設計實現的乘法器性能研究
一種用于SOC中快速乘法器的設計
數字陣列乘法器的算法及結構分析
基于FPGA 的單精度浮點數乘法器設計
基于FPGA的高速流水線浮點乘法器設計與實現
一種高速流水線乘法器結構
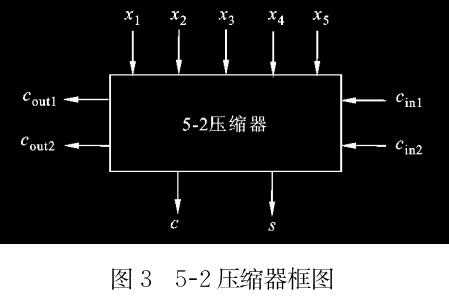
使用verilogHDL實現乘法器
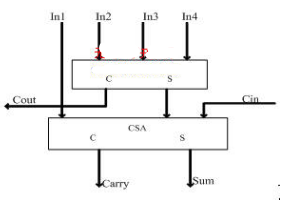
乘法器原理_乘法器的作用





 布斯算法(Booth Algorithm)乘法器的Verilog實現
布斯算法(Booth Algorithm)乘法器的Verilog實現











評論