前兩篇中，我們介紹了諧振電路系統(tǒng)的時(shí)域分析方法和頻域分析方法，并結(jié)合了不同的電路實(shí)例，總結(jié)了軟開(kāi)關(guān)ZVS的實(shí)現(xiàn)條件。我們的思路是從最基本的電力電子電路出發(fā)，逐步將諧振和軟開(kāi)關(guān)的概念引入到PWM電力電子電路中，所以我們重點(diǎn)關(guān)心了電路的模態(tài)和波形等時(shí)域表現(xiàn)。我們從直觀上對(duì)時(shí)域的模型更熟悉，但從電路分析的角度，模態(tài)和波形分析只是在某一個(gè)具體的頻率條件下進(jìn)行的。

對(duì)于諧振電路而言，如果只了解電路的時(shí)域表現(xiàn)，就仿佛是只看到了冰山一角 ，和頻率相關(guān)的大部分知識(shí)都藏在海底。而今天我們需要做的，就是要讓剩下的冰山，全部浮出水面。

一.再論歐姆定律

大家可能覺(jué)得很奇怪，歐姆定律這種初中生就知道的常識(shí)，為什么還要拿來(lái)這里說(shuō)。這里，我們討論的歐姆定律，不再?gòu)臅r(shí)間的角度考慮，而是從頻率的角度考慮，它描述的是電壓和電流的一種線性關(guān)系。比如，在直流穩(wěn)態(tài)電路中，我們知道，要計(jì)算某段導(dǎo)體的電阻，只需要用這段導(dǎo)體兩端的電壓除以流經(jīng)導(dǎo)體的電流即可得到。

那么，當(dāng)我們?cè)谶@段導(dǎo)體上施加的電壓是交流電壓，而且電壓是以正弦波的形式交變，我們還能得到相同的結(jié)論的嗎？如果把這段導(dǎo)體認(rèn)為是理想的純電阻，答案是肯定的。施加頻率為f1的正弦波電壓，就得到頻率為f1的正弦波電流；施加頻率為f2的余弦波電壓，就得到頻率為f2的余弦波電壓。在任何頻率下，電阻兩端的電壓都與流經(jīng)電阻的電流成正比，這個(gè)比例系數(shù)，就是電阻值。

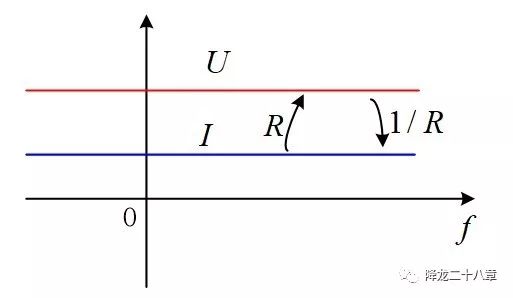
這樣，在整個(gè)頻域，電壓和電流形成了一種映射，而且是一種線性映射，這就是歐姆定律在頻域的本質(zhì)。

但是實(shí)際上，任何導(dǎo)體都不可能是理想的純電阻。

當(dāng)我們把兩端正弦波電壓頻率增高（比如到了100MHz），我們會(huì)發(fā)現(xiàn)流經(jīng)導(dǎo)體的電流的相位和施加的電壓相位有些偏差，學(xué)過(guò)電路理論的人應(yīng)該都知道這是由于導(dǎo)體的高頻感抗造成的。

在一些電工學(xué)的教材中，正弦穩(wěn)態(tài)分析和阻抗的概念被引入。把電壓和電流當(dāng)做旋轉(zhuǎn)矢量這種方法，與我們第一篇提到的簡(jiǎn)諧振動(dòng)旋轉(zhuǎn)矢量類似。

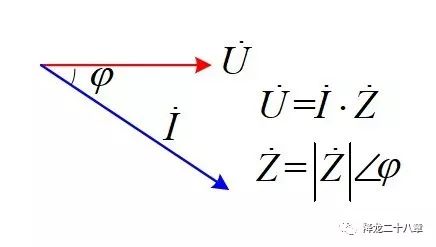
但穩(wěn)態(tài)意味著只在某個(gè)頻率點(diǎn)，我們之前提到，電力電子電路中存在大量的開(kāi)關(guān)動(dòng)態(tài)，一個(gè)開(kāi)關(guān)（階躍）動(dòng)作，就意味著無(wú)數(shù)多個(gè)高頻激勵(lì)分量。這樣，正弦穩(wěn)態(tài)分析的方法不再適用，我們需要找到更廣義的解法--頻域阻抗。

在頻域中，我們假定存在這樣一個(gè)激勵(lì)：激勵(lì)電流Iin(f)=1，即激勵(lì)電流由無(wú)窮多個(gè)頻率下的單位激勵(lì)合成，如果我們想要關(guān)心電路系統(tǒng)在任何頻率下的電壓響應(yīng)，那我們就需要一個(gè)關(guān)于頻率f的阻抗函數(shù)，這個(gè)阻抗函數(shù)不僅要包含在各個(gè)激勵(lì)頻率下的電壓電流幅值的比例系數(shù)信息，還要包含了各個(gè)頻率下電壓電流的相位差信息。

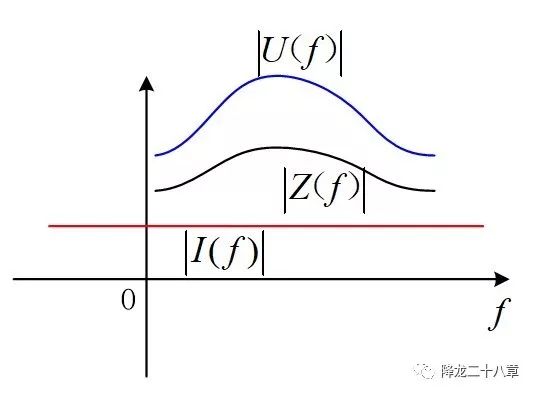
因此，我們需要引入頻域阻抗（或者復(fù)阻抗）的概念。如果說(shuō)正弦穩(wěn)態(tài)分析中的阻抗是海面上我們看得到的冰山，那整個(gè)頻域的頻域阻抗就是包含了海底部分的整個(gè)冰山。

頻域中，電感的阻抗和頻率成正比，這是由電感的充放電關(guān)系決定的

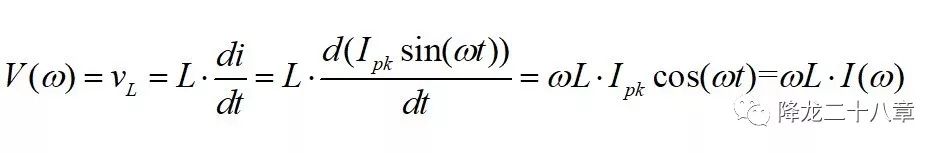
電容的阻抗和頻率成反比，這是由電容的充放電關(guān)系決定的。

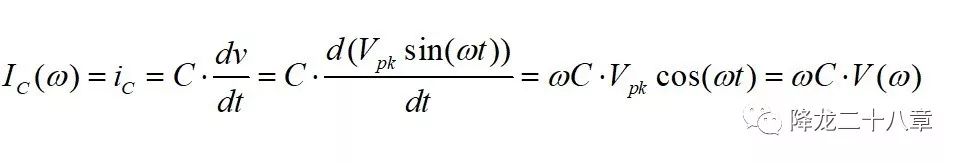
我們知道，諧振網(wǎng)絡(luò)主要是由電感、電容和電阻三種元器件組成，這樣我們可以把諧振網(wǎng)絡(luò)等效成一個(gè)線性二端口網(wǎng)絡(luò)。

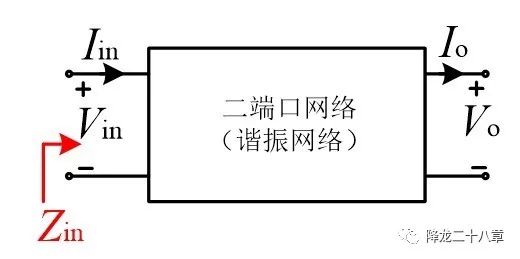
二端口網(wǎng)絡(luò)的左側(cè)認(rèn)為是輸入側(cè)，一般接能量供給單元，例如電壓源，電流源等，右側(cè)認(rèn)為是輸出側(cè)，一般接能量消耗單元，例如電阻（或者等效的電壓源，電流源）。當(dāng)負(fù)載接入后，從左側(cè)看過(guò)去，可以認(rèn)為輸入電流和輸入電壓滿足一定的函數(shù)關(guān)系：

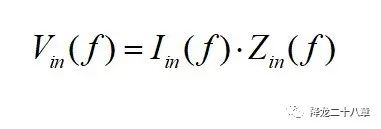
這里的Zin(f)即為這個(gè)二端口網(wǎng)絡(luò)等效的輸入阻抗。它反映了特定負(fù)載條件下，施加不同頻率的激勵(lì)（可以是電壓，也可以是電流），二端口網(wǎng)絡(luò)從輸入端表現(xiàn)出來(lái)的外特性。

怎樣量化這個(gè)阻抗呢？

從電路的頻域模型入手。

比如一個(gè)簡(jiǎn)單的LCR網(wǎng)絡(luò)，容易得到其頻域模型，令初始狀態(tài)為零，可以得到從輸入電流到輸入電壓的傳遞函數(shù)。只需要將傳遞函數(shù)中的s，代換成2πjf,這里的f是頻率，j是單位虛數(shù)。

這樣根據(jù)頻域模型得到的傳遞函數(shù)便有了物理意義，它表示系統(tǒng)在各個(gè)頻率點(diǎn)的輸入阻抗Zin(f）。各個(gè)頻率的輸入阻抗Zin(f)都是復(fù)數(shù)，它的幅值規(guī)定了輸入電壓幅值和輸入電流幅值的比例，幅角定義了該頻率下輸入電壓超前于電流的相位角。

二.正弦波等效分析

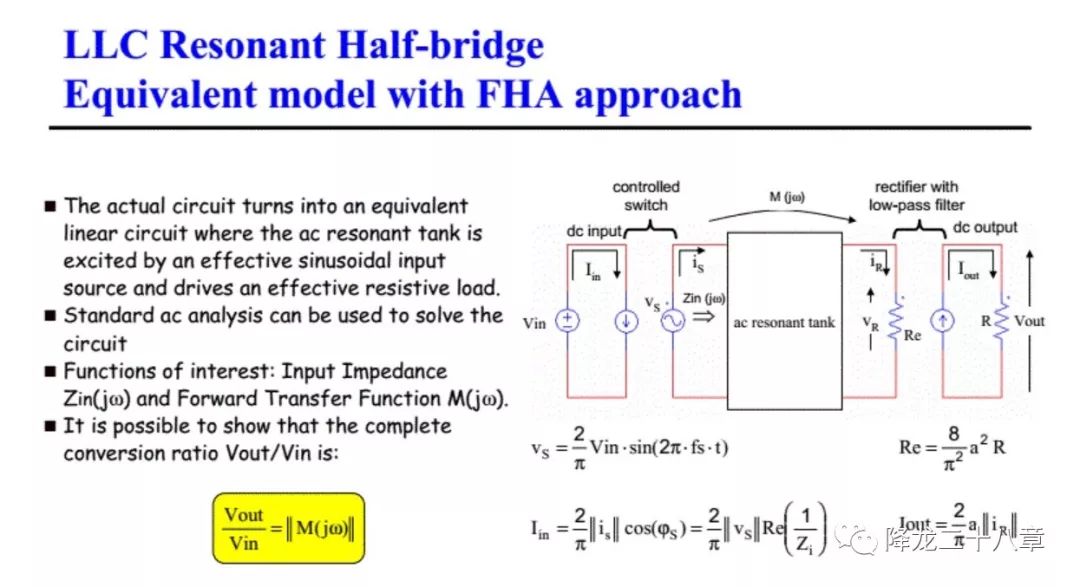
前文中我們講到了諧振網(wǎng)絡(luò)的輸入阻抗概念，接下來(lái)我們便要將這個(gè)概念應(yīng)用到諧振變換器中。以串聯(lián)諧振DC/DC變換器為例，下圖是該變換器的電路拓?fù)洹?/p>

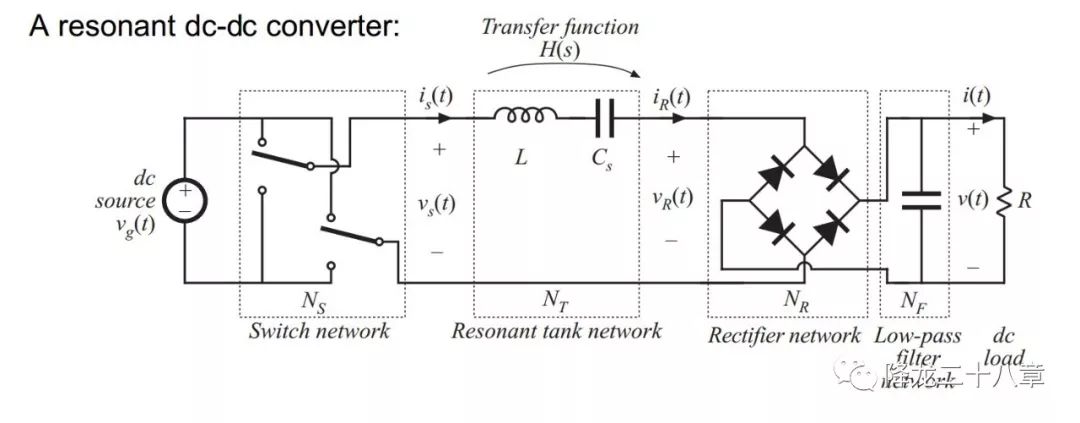
這是一種典型的諧振變換器電路，電路由四個(gè)二端口網(wǎng)絡(luò)構(gòu)成，開(kāi)關(guān)網(wǎng)絡(luò)，諧振網(wǎng)絡(luò)（或者稱諧振腔），整流網(wǎng)絡(luò)，濾波網(wǎng)絡(luò)。

從傳遞函數(shù)的角度來(lái)看，開(kāi)關(guān)網(wǎng)絡(luò)和整流網(wǎng)絡(luò)都是含有開(kāi)關(guān)器件的非線性網(wǎng)絡(luò)，而諧振網(wǎng)絡(luò)和濾波網(wǎng)絡(luò)則是線性網(wǎng)絡(luò)。我們的目的是要從頻域分析整個(gè)電路的特性，所以對(duì)各個(gè)網(wǎng)絡(luò)做單獨(dú)的等效處理，將所有的非線性網(wǎng)絡(luò)等效成線性網(wǎng)絡(luò)。

首先關(guān)注開(kāi)關(guān)網(wǎng)絡(luò)。由于輸入電壓源的存在，開(kāi)關(guān)網(wǎng)絡(luò)的輸出電壓為方波電壓。同時(shí)諧振系統(tǒng)具有選頻特性，可認(rèn)為諧振腔只對(duì)諧振頻率的激勵(lì)進(jìn)行響應(yīng)。 所以我們不妨假設(shè)開(kāi)關(guān)網(wǎng)絡(luò)的開(kāi)關(guān)頻率接近諧振頻率 ，這樣開(kāi)關(guān)網(wǎng)絡(luò)的方波輸出電壓中只有其基波分量被響應(yīng)，其他頻次分量都可忽略。

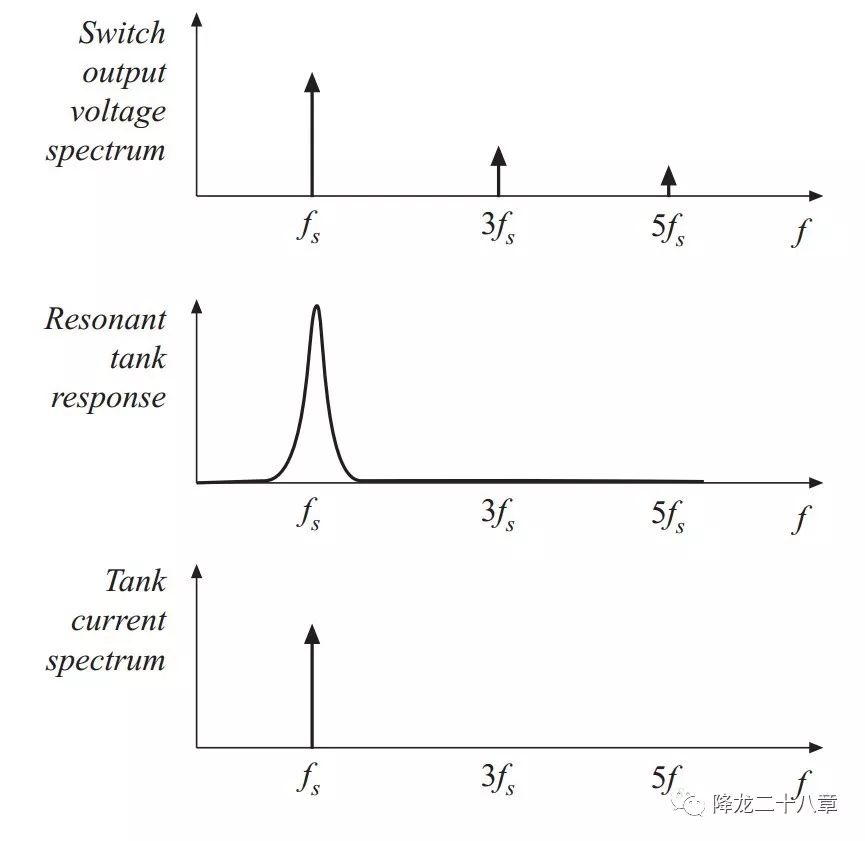
開(kāi)關(guān)網(wǎng)絡(luò)的輸出方波電壓做傅里葉分解后的基波電壓如下

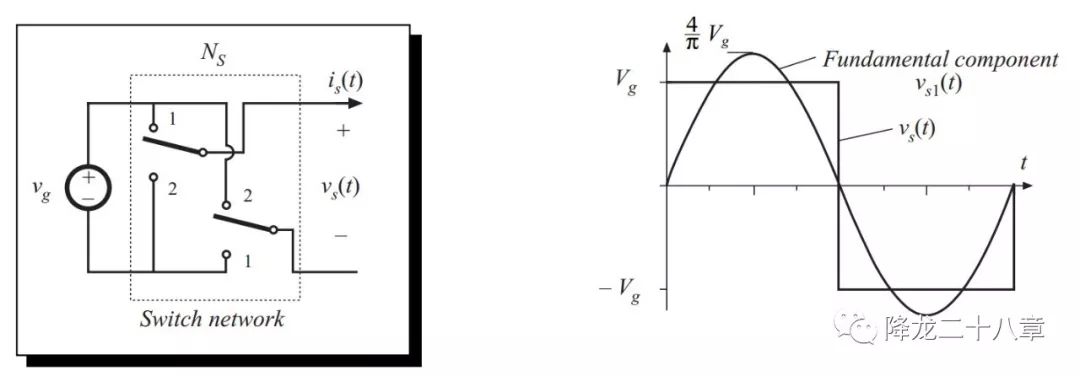
開(kāi)關(guān)網(wǎng)絡(luò)的輸入電流波形如下

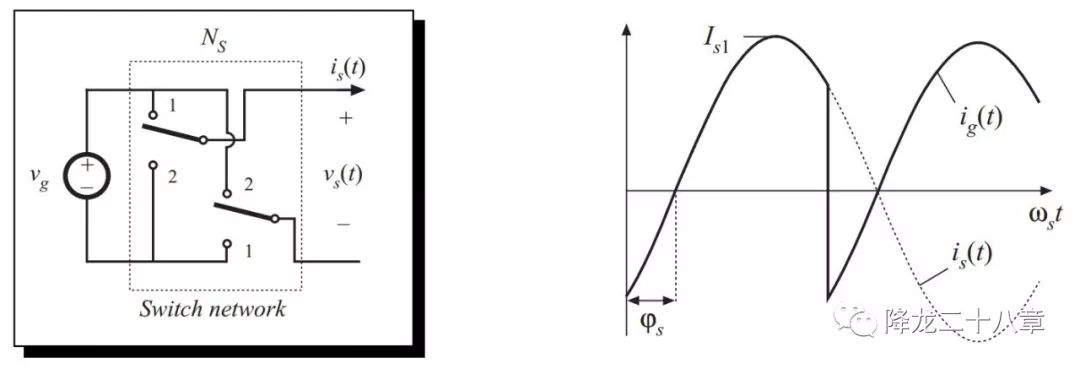
其中，ψs為諧振腔的響應(yīng)電流（同時(shí)也是開(kāi)關(guān)網(wǎng)絡(luò)的輸出電流）滯后于開(kāi)關(guān)網(wǎng)絡(luò)輸出電壓基波的相角，Is1為響應(yīng)電流的幅值。

可以對(duì)開(kāi)關(guān)網(wǎng)絡(luò)輸入電流求取一個(gè)周期內(nèi)的直流分量

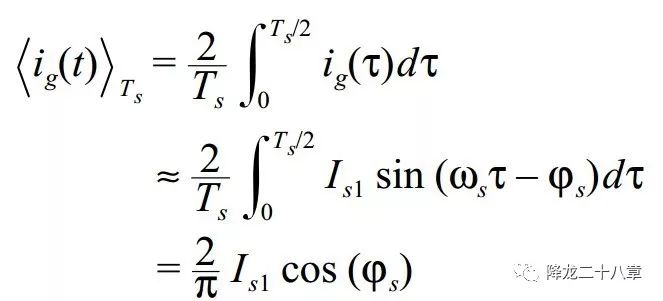
這樣，我們可以把電源及開(kāi)關(guān)網(wǎng)絡(luò)等效成如下形式

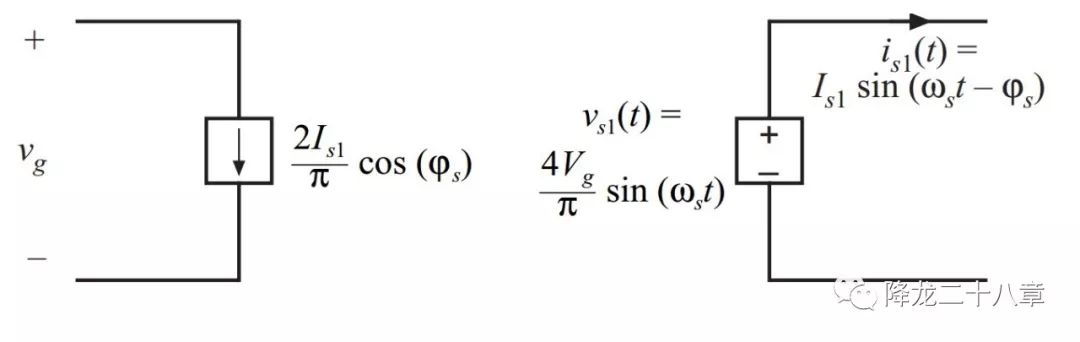
左邊代表直流電源輸出直流電，直流電負(fù)載即為開(kāi)關(guān)網(wǎng)絡(luò)輸入電流的平均值。右邊代表交流電壓源給諧振網(wǎng)絡(luò)輸出交流電，交流電壓源的幅值為開(kāi)關(guān)網(wǎng)絡(luò)輸出方波電壓的基波幅值，交流電頻率為開(kāi)關(guān)頻率。

同樣的方法，我們可以對(duì)整流網(wǎng)絡(luò)和濾波網(wǎng)絡(luò)等效，由于容性負(fù)載的存在，整流網(wǎng)絡(luò)的輸入電壓為方波電壓（V為輸出直流電壓）

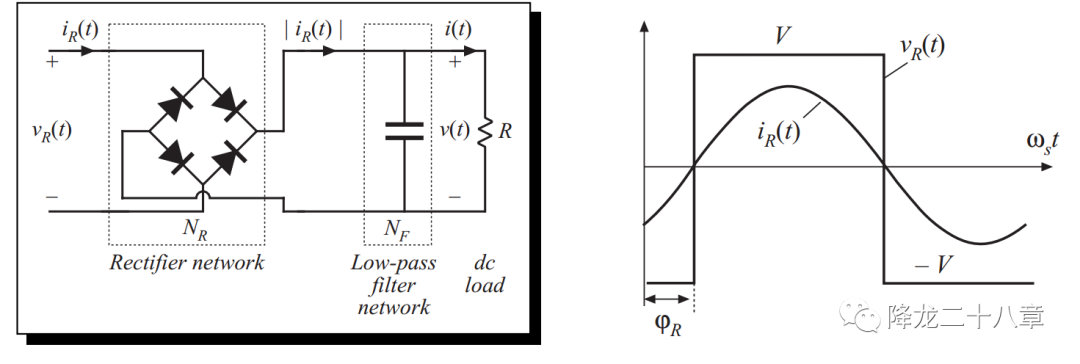
對(duì)整流網(wǎng)絡(luò)的輸出方波進(jìn)行傅里葉分解，

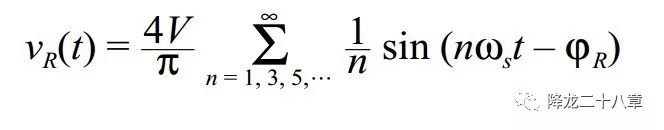
整流網(wǎng)絡(luò)的輸入電流為諧振網(wǎng)絡(luò)的輸出電流，（這里我們考慮的是LC串聯(lián)諧振網(wǎng)絡(luò)，諧振網(wǎng)絡(luò)的輸出電流與輸入電流相等,is1=ir1,ψs=ψr,，如果是其他形式的諧振網(wǎng)絡(luò)，則輸入輸出電流未必相等）：

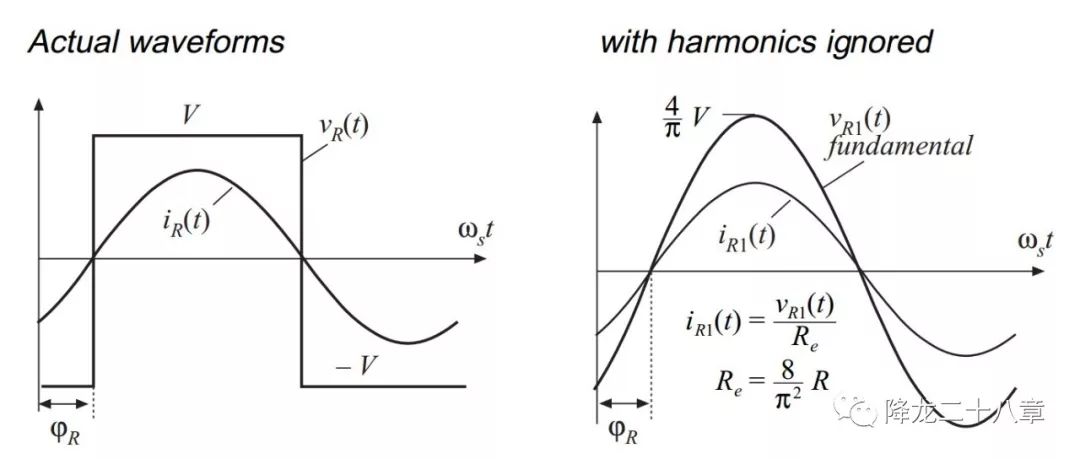
考慮整流網(wǎng)絡(luò)的輸入電壓基波幅值與輸入電流的幅值比例及相位關(guān)系，可以得到的整流網(wǎng)絡(luò)及濾波網(wǎng)絡(luò)（負(fù)載電阻為R）的等效輸入阻抗，這個(gè)阻抗是一個(gè)純電阻，可以表示為Re。

這樣就可以得到由整流網(wǎng)絡(luò)，濾波網(wǎng)絡(luò)及負(fù)載電阻構(gòu)成的等效電路如下圖

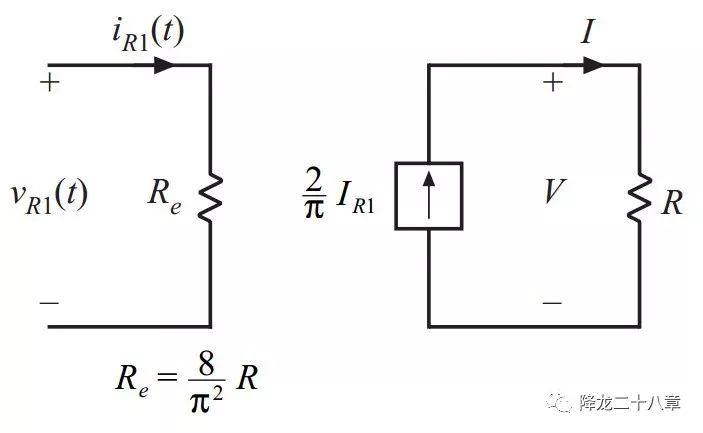
接下來(lái)，我們便可以對(duì)整個(gè)諧振變換器電路進(jìn)行等效，非線性網(wǎng)絡(luò)被等效成了線性網(wǎng)絡(luò)。

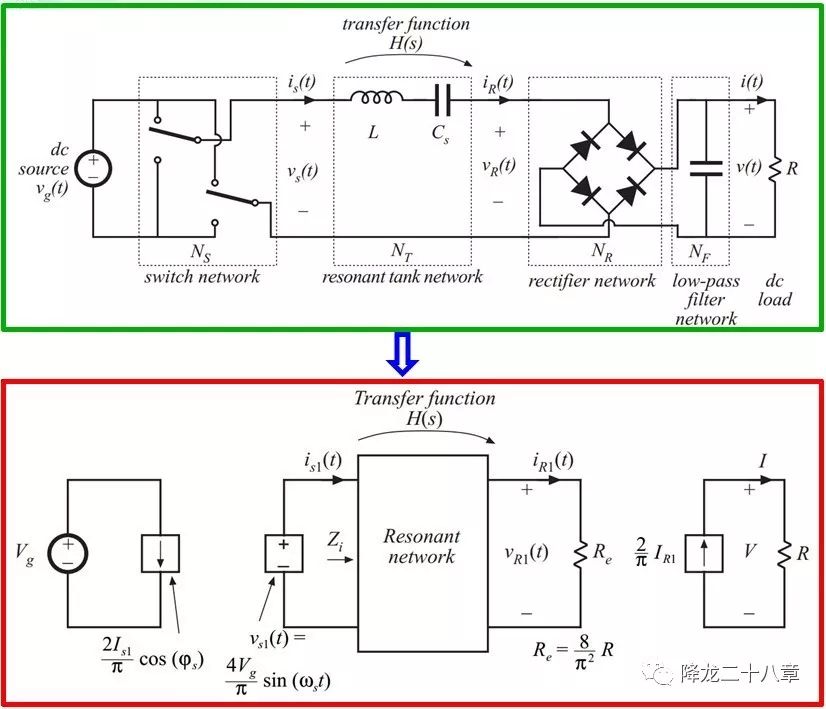
我們只需要關(guān)心等效后的諧振網(wǎng)絡(luò)部分的頻域特性，問(wèn)題被大大簡(jiǎn)化。 這樣的分析方法，被稱為基波等效分析法 。這樣，所有針對(duì)諧振變換器的分析工作，都可以圍繞諧振網(wǎng)絡(luò)的特性展開(kāi)。

那么我們需要關(guān)心諧振網(wǎng)絡(luò)的哪些特性呢？

1. 阻抗特性。分為輸入阻抗和輸出阻抗，輸入阻抗的幅值決定了輸入電流對(duì)輸入電壓的響應(yīng)比例，這對(duì)于開(kāi)關(guān)管的電流應(yīng)力是決定性因素；輸入阻抗的相角是實(shí)現(xiàn)開(kāi)關(guān)管軟開(kāi)關(guān)的關(guān)鍵因素；對(duì)于輸出阻抗，則決定了系統(tǒng)的阻抗匹配，當(dāng)系統(tǒng)輸出阻抗成純阻性時(shí)，這時(shí)調(diào)節(jié)負(fù)載等效電阻Re，使其等于輸出阻抗，Re變能獲得最大的輸出功率。
2. 增益特性。這個(gè)諧振變換器例子中的輸出為電壓源型負(fù)載，穩(wěn)態(tài)的輸出電壓V與輸入電壓Vg的比例是這個(gè)電路的增益M，這個(gè)增益顯然和諧振網(wǎng)絡(luò)的輸入輸出電壓傳遞函數(shù)H(s)有關(guān)。

以串聯(lián)諧振變換器為例，輸入輸出電壓增益M等于諧振網(wǎng)絡(luò)輸入輸出電壓傳遞函數(shù)H(s)的幅值（證明如下圖），

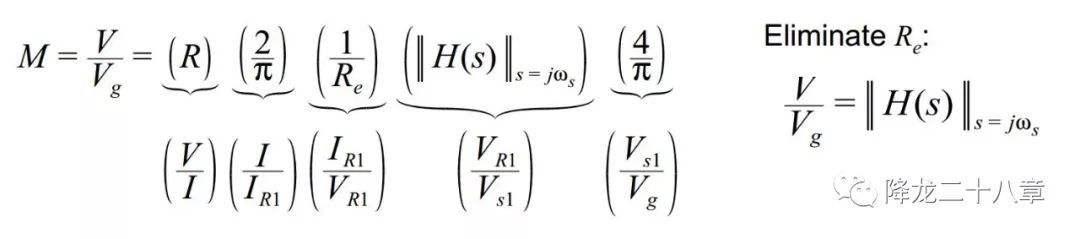
下圖為串聯(lián)諧振變換器的諧振網(wǎng)絡(luò)輸入輸出電壓傳遞函數(shù)。

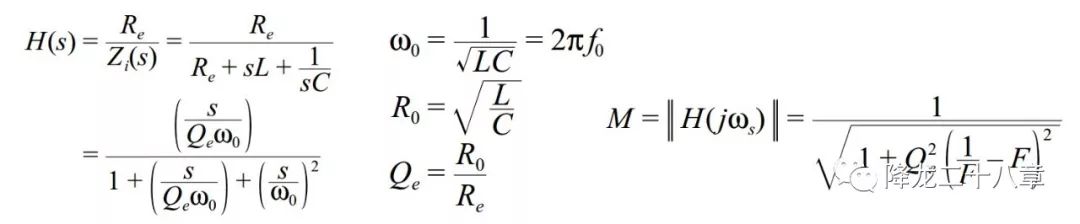
除了公式表示以外，還可以通過(guò)曲線圖表示增益特性和阻抗特性

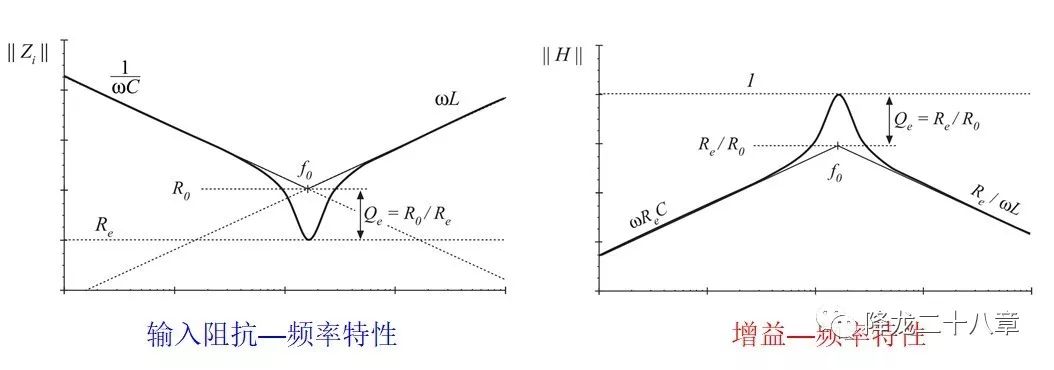
以上兩點(diǎn)就是阻抗特性和增益特性分析諧振變換器的 兩大利器 。可以看到，這兩個(gè)特性都是和開(kāi)關(guān)頻率相關(guān)的，可以寫成開(kāi)關(guān)頻率的函數(shù)，這就是典型的頻域分析。

值得注意的是，傳遞函數(shù)這種頻域函數(shù)只有在把自變量s換成了2πjf時(shí)才具有明確的物理意義。并且，傳遞函數(shù)是基于零初始狀態(tài)的條件得到的，當(dāng)系統(tǒng)的初始條件不可忽略時(shí)，傳遞函數(shù)的方法便不再適用，這時(shí)再采用時(shí)域微分方程結(jié)合電路模態(tài)分析是一種解法，但更多的時(shí)候，使用狀態(tài)空間的方法會(huì)更簡(jiǎn)潔，有興趣的讀者可以參考現(xiàn)代控制理論的相關(guān)內(nèi)容，這里不再贅述。

三.LLC電路實(shí)例

前文中，我們以串聯(lián)諧振變換器為例，給出了諧振變換器的頻域分析方法--基波等效分析法。這部分內(nèi)容都是在從數(shù)學(xué)的角度建立模型，說(shuō)白了就是空洞洞的理論。現(xiàn)在，我們便將這一理論應(yīng)用到一個(gè)非常典型的實(shí)際變換器中，畢竟，實(shí)踐是檢驗(yàn)理論的唯一標(biāo)準(zhǔn)嘛。

提起LLC諧振變換器，相信大家都有所了解。業(yè)內(nèi)有非常多的產(chǎn)品和研究工作就是基于LLC諧振變換器的，所以今天我們不再對(duì)它的電路模態(tài)這些細(xì)節(jié)做詳細(xì)的介紹了。

我們把前文提到的兩大利器應(yīng)用到這個(gè)電路里面，讓大家理解這個(gè)變換器最基本的道理就Ok。

如果看官們對(duì)LLC變換器的相關(guān)知識(shí)感興趣，我給各位推薦兩份資料，第一份是意法半導(dǎo)體（ST）制作的LLC分析文檔，在百度文庫(kù)上可以查到；第二份是一篇博士論文，題為Investigation of High-density Integrated Solution for AC/DC Conversion of a Distributed Power System。

首先，我們來(lái)看全橋LLC諧振DC/DC變換器的電路拓?fù)浣Y(jié)構(gòu)

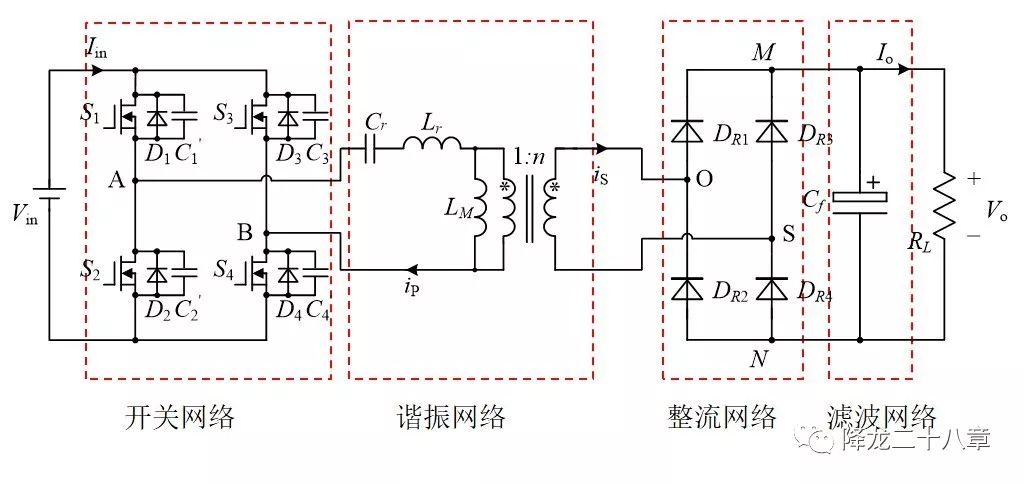
可以看到，這個(gè)變換器的結(jié)構(gòu)與前文中的串聯(lián)諧振變換器一樣，可以分為開(kāi)關(guān)網(wǎng)絡(luò)，諧振網(wǎng)絡(luò)，整流網(wǎng)絡(luò)和濾波網(wǎng)絡(luò)四個(gè)二端口網(wǎng)絡(luò)。不同的是，這個(gè)電路拓?fù)涞闹C振網(wǎng)絡(luò)是一個(gè)帶變壓器的二端口網(wǎng)絡(luò)，并且有三個(gè)諧振元件，諧振電感，諧振電容，變壓器勵(lì)磁電感。

由于結(jié)構(gòu)與上文分析的一致性，我們可以把上文中的分析方法應(yīng)用到這個(gè)LLC拓?fù)渲校瑯雨P(guān)注諧振網(wǎng)絡(luò)的頻域特性。

和上一篇一樣，我們?cè)倏纯碙LC諧振變換器的ZVS條件。

我們知道，諧振網(wǎng)絡(luò)的輸入電壓基波與輸入電流存在相位角，這個(gè)相位角就是輸入阻抗在基波頻率點(diǎn)的相位角。

那么這個(gè)相位角對(duì)于開(kāi)關(guān)網(wǎng)絡(luò)意味著什么呢？

如下圖，紅色為方波輸入電壓，藍(lán)色為原邊的諧振電流，圖中表現(xiàn)的是電流相位滯后于電壓相位的情形。當(dāng)VAB為負(fù)向輸入電壓時(shí)，表示2，3管導(dǎo)通，要么是2，3管的溝道導(dǎo)通電流，要么是2，3管的寄生二極管導(dǎo)通，可根據(jù)電流方向區(qū)分。當(dāng)2,3管同時(shí)關(guān)斷后，考慮死區(qū)時(shí)間，1，2，3，4管都是處于關(guān)斷狀態(tài)。如果此時(shí)的諧振電流為負(fù)值，便會(huì)給2，3管結(jié)電容充電，給1，4管結(jié)電容放電，如果能量足以將1，4管結(jié)電容電壓降至零，再經(jīng)1，4管的寄生二極管續(xù)流，便具備了實(shí)現(xiàn)軟開(kāi)關(guān)ZVS的條件。

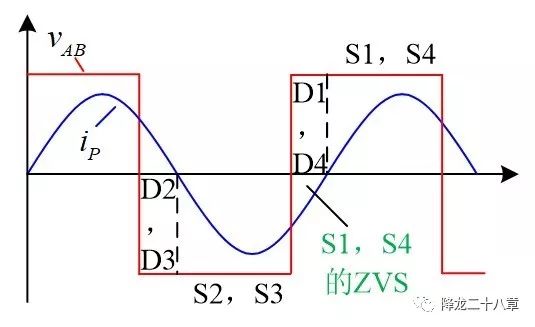
接下來(lái)是電流超前于電壓的情況。如下圖，在VAB為負(fù)輸入電壓時(shí)，2，3管先由溝道導(dǎo)通負(fù)向電流，再由寄生二極管導(dǎo)通正向電流。電流從溝道換向二極管的過(guò)程，電流從峰值降到零，再變?yōu)樨?fù)向，是一個(gè)自然換流的過(guò)程，此時(shí)即使S2,S3的驅(qū)動(dòng)為高，電流也不再通過(guò)溝道流通。二極管續(xù)流一段時(shí)間后，S2，S3驅(qū)動(dòng)變低，關(guān)斷S2,S3，這就實(shí)現(xiàn)了S2,S3管的ZCS。關(guān)斷S2,S3后，經(jīng)過(guò)短暫的死區(qū)時(shí)間后再開(kāi)通S1,S4。S1,S4開(kāi)通時(shí)，二極管S2,S3還流通正向電流，但其電壓迅速上升至輸入電壓，強(qiáng)制S2,S3關(guān)斷，這時(shí)D2,D3會(huì)產(chǎn)生嚴(yán)重的二極管反向恢復(fù)問(wèn)題，而此時(shí)S1,S4已開(kāi)通，相當(dāng)于橋臂形成直通，如果能量足夠大，就有損壞器件的風(fēng)險(xiǎn)。另外，反向恢復(fù)過(guò)程還伴隨較嚴(yán)重的電壓震蕩問(wèn)題，不僅增加了損耗，而且可能超過(guò)器件的安全工作區(qū)導(dǎo)致失效。 所以ZCS的情況需要盡量避免。 這部分內(nèi)容在我推薦的第一份資料里有詳細(xì)的介紹，大家可以參考。

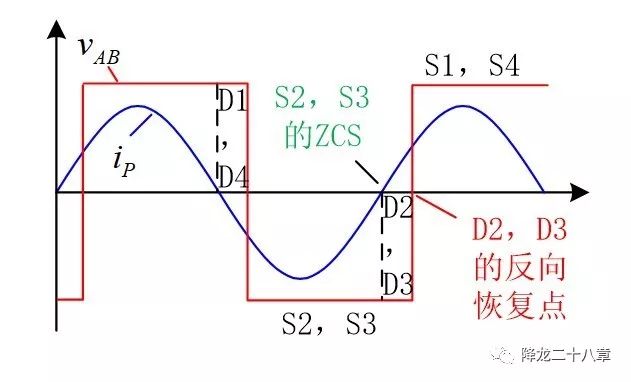
一般的LLC諧振變換器設(shè)計(jì)，會(huì)規(guī)定感性區(qū)和容性區(qū)，就是從輸入阻抗的角度考慮的，因?yàn)楦行詤^(qū)意味著電流相位滯后于電壓相位，可以實(shí)現(xiàn)ZVS。而容性區(qū)則意味著電流相位超前于電壓相位，是ZCS區(qū)，需要避免。

上文中我們討論了輸入阻抗特性對(duì)于開(kāi)關(guān)網(wǎng)絡(luò)ZVS的實(shí)現(xiàn)的作用，下面我們討論增益特性對(duì)系統(tǒng)的影響。

下圖是LLC變換器的歸一化增益曲線，所謂歸一化，就是將橫坐標(biāo)的開(kāi)關(guān)頻率fs換成了開(kāi)關(guān)頻率與諧振頻率的比值fn。另外，我們把勵(lì)磁電感Lm與諧振電感Lr的比例記為k，諧振網(wǎng)絡(luò)特征阻抗與等效電阻Re的比值記為Q，可以得到增益函數(shù)是關(guān)于fn,k,Q的函數(shù)M（fn,k,Q)

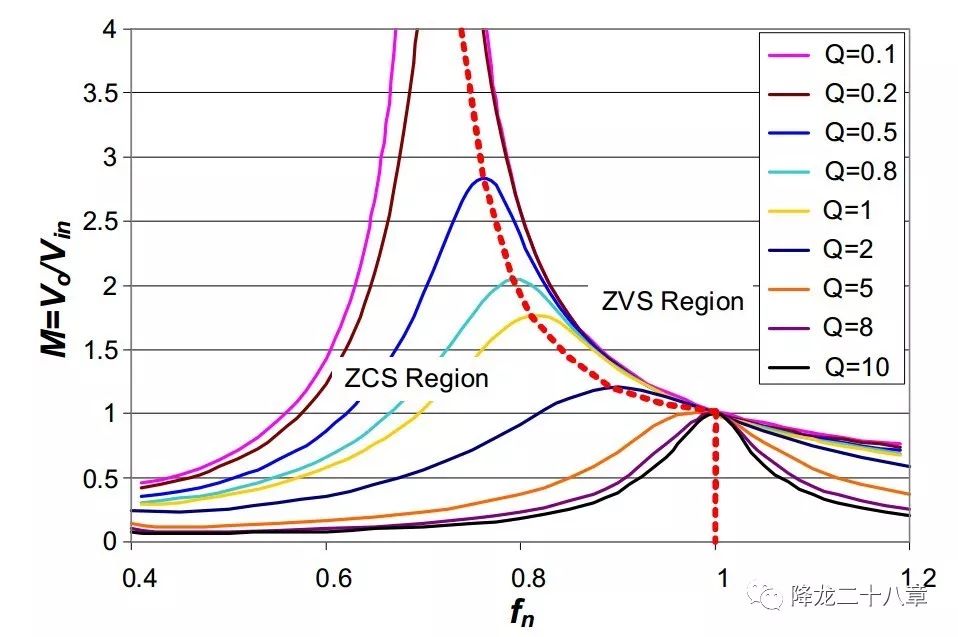
圖中紅色虛線為輸入阻抗的純阻性曲線，曲線的右邊意味著感性區(qū)和ZVS，右邊意味著容性區(qū)和ZCS。

值得注意的是，這個(gè)曲線是在某個(gè)特定的k下得到的，也就是說(shuō)，改變勵(lì)磁電感與諧振電感的比例，增益曲線的形狀也會(huì)變化。

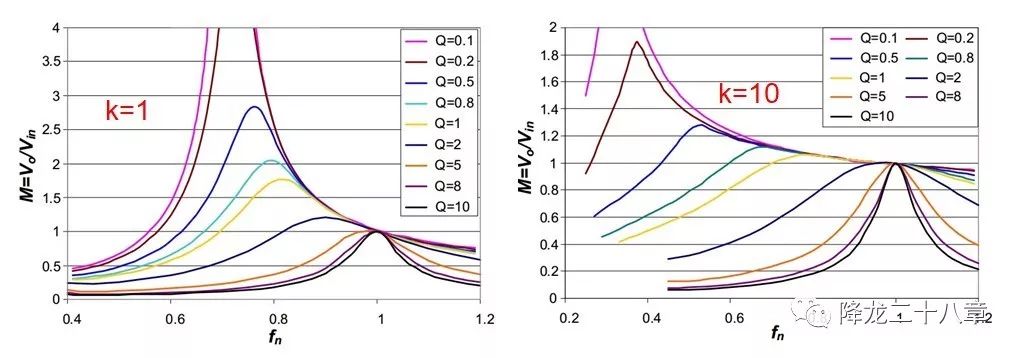
從圖中可以看到，當(dāng)k值變大后，增益曲線變“平坦”，這意味著要獲得相同的增益變化范圍，k值大的諧振網(wǎng)絡(luò)需要的頻率變化范圍比k值小的諧振網(wǎng)絡(luò)需要的頻率變化范圍更大。這即是我們所說(shuō)到的敏感性，LLC諧振變換器的增益對(duì)開(kāi)關(guān)頻率的敏感性是和k值相關(guān)的。

在一些恒流輸出場(chǎng)合，比如3.3kW的恒流輸出的車載充電器，經(jīng)過(guò)PFC整流后的母線電壓是380V-420V直流，要通過(guò)LLC諧振變換器轉(zhuǎn)化成70V-120V/30A的直流電壓電流給電池供電，再比如中大功率恒流型LED驅(qū)動(dòng)電源，同樣PFC后的直流母線電壓需要轉(zhuǎn)化成20-48V的直流電壓。這些場(chǎng)合輸出電壓變化范圍寬，需要的電路增益變化范圍較大，而控制器的開(kāi)關(guān)頻率變化范圍是有限的。這時(shí)可以使用k值較低的諧振網(wǎng)絡(luò)，使得開(kāi)關(guān)頻率的變化范圍在控制器的輸出能力之內(nèi)。

但如果k值過(guò)小，會(huì)有什么問(wèn)題？

k值較小，意味著勵(lì)磁電感相對(duì)于諧振電感較小，勵(lì)磁電流相對(duì)于諧振電流不可忽略。變換器進(jìn)入輕載時(shí)，勵(lì)磁電流帶來(lái)的磁芯損耗較大。另外，原邊電流中激磁電流的成分多，同時(shí)也增加了高頻線損。下圖為勵(lì)磁電感較小（k=2)的一個(gè)例子，紅色為橋臂中點(diǎn)電壓VAB，黃色為原邊電流ip。

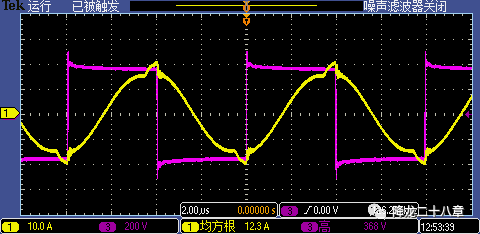
事實(shí)上，當(dāng)我們規(guī)定了電路需要的最低增益，諧振頻率和允許的最高開(kāi)關(guān)頻率后，我們可以定量地計(jì)算得到k值，具體參考ST的LLC文檔。但在電路調(diào)試的過(guò)程中也會(huì)看到k值的影響，不止是在損耗和效率方面，k值對(duì)控制電路，電壓應(yīng)力等都是非常重要的。我們往往會(huì)對(duì)k值有一個(gè)預(yù)期，根據(jù)工程師經(jīng)驗(yàn)，可以大概給出一個(gè)特定場(chǎng)合應(yīng)用的k值范圍。至于合不合理，就要看工程師的道行了。感興趣的讀者可以繼續(xù)深入地分析k值對(duì)電路方方面面的影響。

對(duì)于LLC的具體設(shè)計(jì)，我提到的兩篇文檔中都有足夠詳細(xì)的內(nèi)容，所以我不再多說(shuō)。文檔中提到的都是恒壓輸出的應(yīng)用場(chǎng)合，感興趣的讀者可以思考恒流輸出應(yīng)用場(chǎng)合的設(shè)計(jì)有何異同。我們只提示大家一個(gè)方法，就是 尋找設(shè)計(jì)的邊界條件 ，比如增益邊界，最高開(kāi)關(guān)頻率，最大功率范圍（空載到滿載），ZVS實(shí)現(xiàn)條件。 如果弄清楚了各個(gè)邊界與我們提到的Q值，k值等頻域參數(shù)的關(guān)系，設(shè)計(jì)就迎刃而解了 。

總結(jié)

以上，我們把頻域的分析方法應(yīng)用到了串聯(lián)諧振拓?fù)浜统Ｓ玫腖LC拓?fù)渲校攸c(diǎn)關(guān)注了基波分析法的由來(lái)和阻抗特性，增益特性在變換器中的體現(xiàn)，希望大家看了之后看清諧振變換器的本質(zhì)，不再被這些復(fù)雜的公式和流程嚇倒。