穩定的概念廣泛存在于各個領域，大到飛機火箭橋梁建筑，小到生活中常見的各類電子產品生活用品，只要涉及到“可控”的要求，一定會談到穩定性（Stability）。科學上，穩定性這種說法被歸到了自動控制原理的范疇。

今天我們就帶大家一起看看，控制上是怎么描述穩定性這件事情，希望能為大家的工作提供一些參考。

穩定性的概念涉及到很多理論知識，但太多的公式會把人繞暈，所以我們接下來多放圖，只在必要的地方放入公式。如果大家很感興趣，后面我們再從理論給出嚴格的推導。

首先，我們看下圖，哪種顏色的球的狀態當前是穩定的呢？

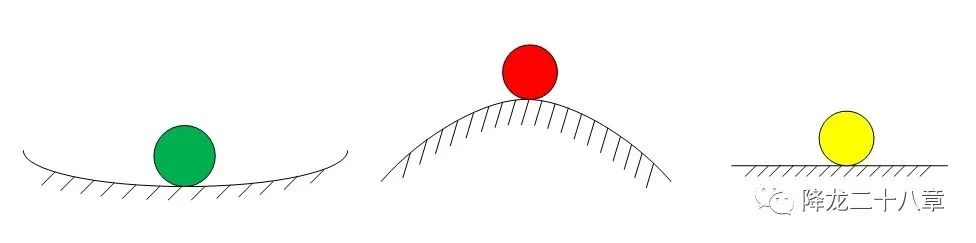
憑直覺，我相信大家都能猜到答案是綠球。

那么為什么認為綠球是穩定的呢，因為支撐它的地面是凹陷的。你給他一個小擾動，他最終還能回到原來的位置。不難發現，小球的穩定狀態是由底面的結構決定的，與施加給小球的擾動無關。

穩定性是系統自身的性質，與系統的輸入輸出無關。

如何判斷一個系統是否穩定呢？

時域到頻域的映射，是通過拉普拉斯變換完成的。這樣的拉式算子模型不僅可以存在于電路系統中，實際上，拉氏算子對任何經典線性控制領域的系統都是適用的。

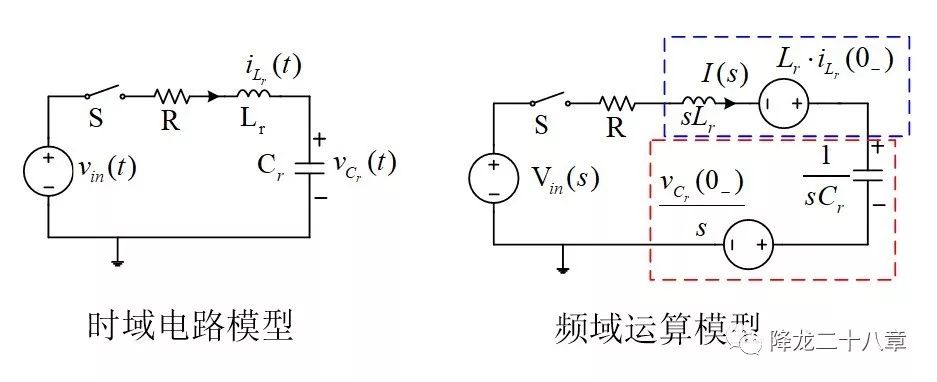
經典控制理論給出的方法是從系統的特征方程入手。這樣的方法是基于：任何含有n個獨立的一階常系數微分方程的方程組，最后都可以將其轉化成一個n階微分方程 。特征方程就是這個方程。拉氏算子，只是一個微分符號。

例如，一個二階LCR系統，其電容充放電關系和電感充放電關系構成的微分方程組就能構成一個二階微分方程。

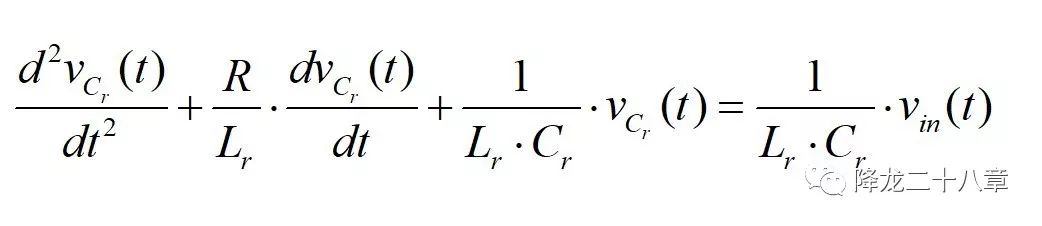
經典控制的所有理論，都是基于常系數線性微分方程的理論。但是單純的微分方程，不具備任何物理意義。

因此控制理論中引入了極點的概念。

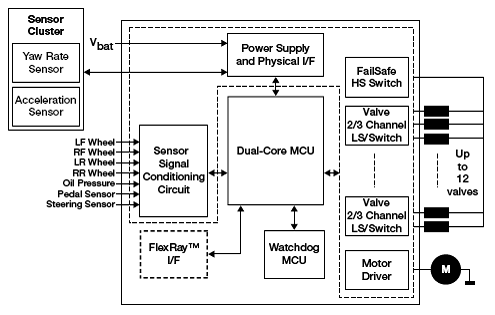
最簡單的極點，就是一階慣性環節的極點。在電路中，一階慣性環節一般是由電阻和電容組成或者由電阻和電感組成。考慮下面這樣一個電路：

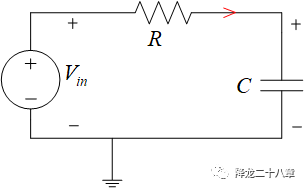
假設初始狀態電壓源輸入為5V，且電路達到穩定，電容C的電壓為5V，電阻電流為零。這時，我們給輸入電壓一個幅值為1V，脈寬為1ms的脈沖擾動。考慮上升沿的過程，由于電容電壓不能突變，故電阻R兩端形成5V的電壓差，產生了電流，流進電容C（給電容充電）。

由于電容C的電荷量增加后其兩端電壓也增加，這樣左邊的電壓源電壓與右邊的電容電壓越來越小，充電電流越來越小，不久后就會形成一個新的穩態，即輸入和電容電壓均為6V，電流為零。下降沿亦是同理，電壓最終回到5V。

我們對這種簡單的一階RC環節的系統方程可以說非常熟悉了，完全可以根據RC參數直接寫出電容電壓的表達式。從系統的特征方程出發，我們可以看到，這個系統僅存在一個極點，并且這個極點是在復平面（s平面）的負實軸上的。這個極點和RC常數相關。但這里我們不關心解析的結果，只關心這個過程對應的物理概念。

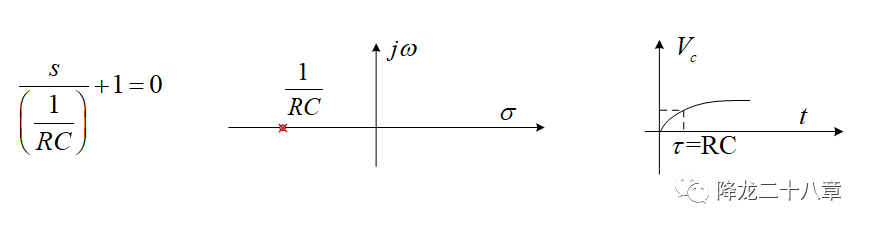
現在的問題是，這個RC系統中輸出能夠跟蹤輸入的最重要條件是什么？

--是電容的充放電特性。

怎樣理解？因為給電容通正電流時，電容兩端電荷積累，其電壓升高，反過來再減小了電阻上的壓差，從而減小電流，這本質上是一種負反饋。

倘若上圖右邊的元件不是電容元件，而是一種通入電荷，電壓變低的特殊元件，那么這個負反饋就成了正反饋，不再具有收斂特性。

所以，一階RC系統的負半平面的單極點至少具備這兩個物理意義：

1）具有收斂特性，對應的是能量的損耗。

2）極點離虛軸越遠，延時效果越差，離虛軸越近，延時效果越好。

經典控制系統一般考慮單輸入單輸出情況，因此可以認為一個復雜系統由多個子系統級聯而成，系統的傳遞函數的分母都可以化成單個極點的乘積。因此，經典控制給出結論：系統穩定的充要條件是所有極點都在s平面的負半平面。

線性系統如果產生了正半平面極點，必定是不穩定和發散的。前文中的特殊元件是一個例子，還有其他一些反饋機制，也能形成不穩定和發散，這里不再舉例。

"所有極點位于負半s平面"這樣的穩定性判據雖然直觀，但是涉及的計算量卻是極大的，特別是當系統階數比較高的時候，求取極點談何容易！