IEEE 1241-2000標準給出的相干采樣定義如下:

下面使用以上符號從原理上對相干采樣進行解釋,需要注意fr定義為波形周期的倒數,若輸入信號為連續的正弦波,fr就是其頻率。
首先介紹應用背景,在測試ADC的動態參數時,一般使用大幅度的正弦波作為輸入信號,該信號的頻率不能任意取,需要滿足相干采樣的要求。連續的正弦波輸入ADC后量化得到一個離散時間信號,之后通過DFT得到信號的頻譜從而進行參數的分析計算。
下面對DFT作一簡要說明,DFT的處理對象為有限長的離散時間信號,若待處理信號是一個非周期信號,那么其頻譜理論上是連續周期的,然而DFT只能得到在i*fs/M(i=0,1…,M-1)這些頻點處的值,但若待處理信號是一個周期信號的單周期的加窗截取,那么其頻譜就是離散周期的,此時DFT在本質上與DFS并無區別,換句話說,DFT得到的結果就是該周期離散時間信號的準確無誤的頻譜。
由于測試的輸入就是一個周期信號,那么根據上述理論,只需要采樣整數個周期,就可以保證得到準確無誤的頻譜。若不是整數個周期,那么就會產生比較嚴重的頻譜泄露現象,實際上DFT將這非整數個周期的信號看作一個周期進行了DFS,顯然,這樣不可能得到正確的頻譜。
那么就可以得到上述公式,總的采樣時間M/fs等于整數個信號周期J/fr。需要注意,該公式也表明頻譜中第J-1(0開始)根譜線正好為輸入信號的頻率。
從另一個角度來說,正弦信號只存在一個固定頻率分量fr,而DFT受限于柵欄效應看不到所有的頻率處的譜線,因此為了能夠看到這個正弦信號的譜線,就需要保證正好有一個點采在fr處,也即fr/(fs/M)=J為一個整數。
另外,一般要求J和M互質,否則會導致某幾個周期采到一樣的點,從而進行無意義的計算,降低效率(e.g.對一周期信號采1個周期4個點和采兩個周期8個點進行FFT,二者頻譜形狀并無區別,后者僅僅是幅度加倍,多的點幅值為0)。
審核編輯:黃飛
-
正弦波
+關注
關注
11文章
650瀏覽量
56195 -
adc
+關注
關注
99文章
6616瀏覽量
547896 -
頻譜
+關注
關注
7文章
893瀏覽量
46251
發布評論請先 登錄
VirtualLab Fusion應用:相干時間和相干長度計算器
VirtualLab Fusion應用:相干時間和相干長度計算器
什么是數字相干檢波?
數字方法中頻信號相干檢波實現
多相濾波技術在數字相干檢波中的應用及FPGA實現
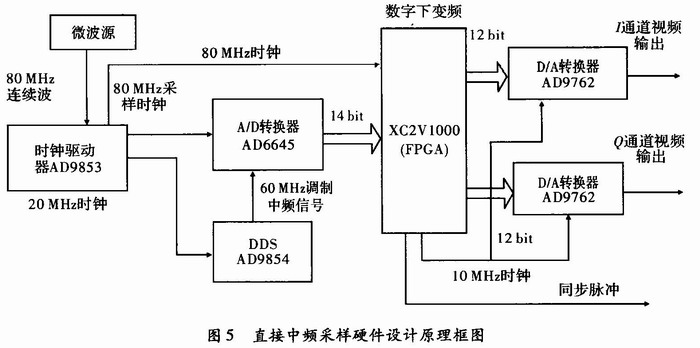
接收相參雷達相干檢波改進設計
相干光通信原理

AN-1388: 使用AD7779 24位同步采樣Σ-型ADC實現電能質量測量的相干采樣








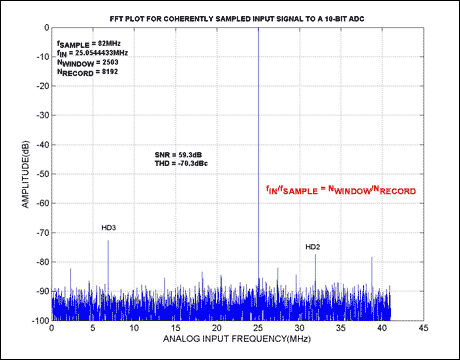











評論