1、前言

在工業應用中，低速率，大規模和長距離的無線自組織網絡一直沒有得到廣泛的部署，根本原因在于其穩定性，可靠性和實時性一直無法得到良好的保證。在這種自組織網絡中，節點之間的跳轉關系大多是根據其相對位置和信號強度來決定的；由于安裝位置，部署密度，啟動時間等差異，其網絡拓撲往往會有比較明顯的不同，在網絡的某些分支，其跳數可能會比較淺，比如1-2跳，而有些分支則比較深，比如6-8跳。在這些網絡跳數比較淺的區域，其丟包率比較小，通訊延遲比較小，可靠性和實時性也比較好；而在那些網絡跳數比較深的區域，其丟包率也比較高，通訊延遲比較大，可靠性和實時性自然也就比較差。

2、業內問題

作為一個上層的應用系統，用戶在設定數據傳輸頻率（是每秒給目標節點發出去多少個應用層的數據包，不是網絡本身的無線通訊速率）的時候，往往是不太關心網絡的拓撲結構的；實際上這個也沒辦法關心，因為它本身就不太固定，因此在設定重傳的時間門限的時候，往往不能充分地考慮到不同的網絡跳數所導致的通訊延遲和丟包率。一旦設置不合理，就會形成嚴重的應答超時和通訊失敗；即便設置了正確的時間參數，由于開放的無線信道經常會受到外界的擾動，這個網絡拓撲可能還會發生變動，更別說因為用戶后期追加設備或者臨時對某些設備二次上電所導致的拓撲結構發生改變了。

從自組織網絡的基本工作原理，我們可以看出，網絡跳數的深淺是由部署環境和一些其他因素綜合決定的，存在較大的偶然性和不確定性。在網絡的某些物理分支，其網絡跳數必定比其他區域更深，這個區域的丟包率，通訊延遲也必然比其他的區域更大，帶來的可靠性和實時性也自然更差。這一點我們可以通過數學上的概率論予以解釋。

3、概率分析

在特定的電磁環境中，每種配置參數的無線通訊系統有一個大致確定的比特誤碼率 BER（Bit Error Rate） 和包誤碼率PER（Packet Error Rate），二者之間有下述關系：

PER=1 - ( 1 – BER )?

其中n是這個數據包的長度，也就是總的比特數量。

考慮到無線自組網系統都是基于數據包作為基本的收發單元，因此本文選定 PER作為分析的依據。為了敘述方便，我們假定丟包率PER為p，那么通訊成功的概率P1，也就是不丟包概率為100% - p，也就是 1-p；對于一個兩跳的無線網絡，要想實現端到端的成功傳輸，那么這連續兩跳都必須傳輸成功，依據概率論的知識，其成功的概率P2應該等于兩跳成功概率的乘積，也就是

P? = P? * P? = P?2 = ( 1 – p )?

同理，對于一個由n+1個節點組成 n跳的多跳無線鏈路，最終的目標節點要想正確地接收到源節點發出來的數據，要求從2號節點到n+1號節點的每一個中間節點都必須正確地收到上一跳發過來的數據，只要有一個環節失敗了，最終的目標節點就無法正確地收到源節點發出來的數據，因此其總的通訊成功率Pn，按照概率論的知識應該有下述關系：

Pn= ( P? * P? …. * P?) = P?? = ( 1 – p )?

為了更加直觀的說明真實的通訊效果，我們以包誤碼率 PER為10%，也就是 p=0.1的電磁環境為例，計算出不同網絡跳數下的鏈路通訊成功率，具體如下表所示：

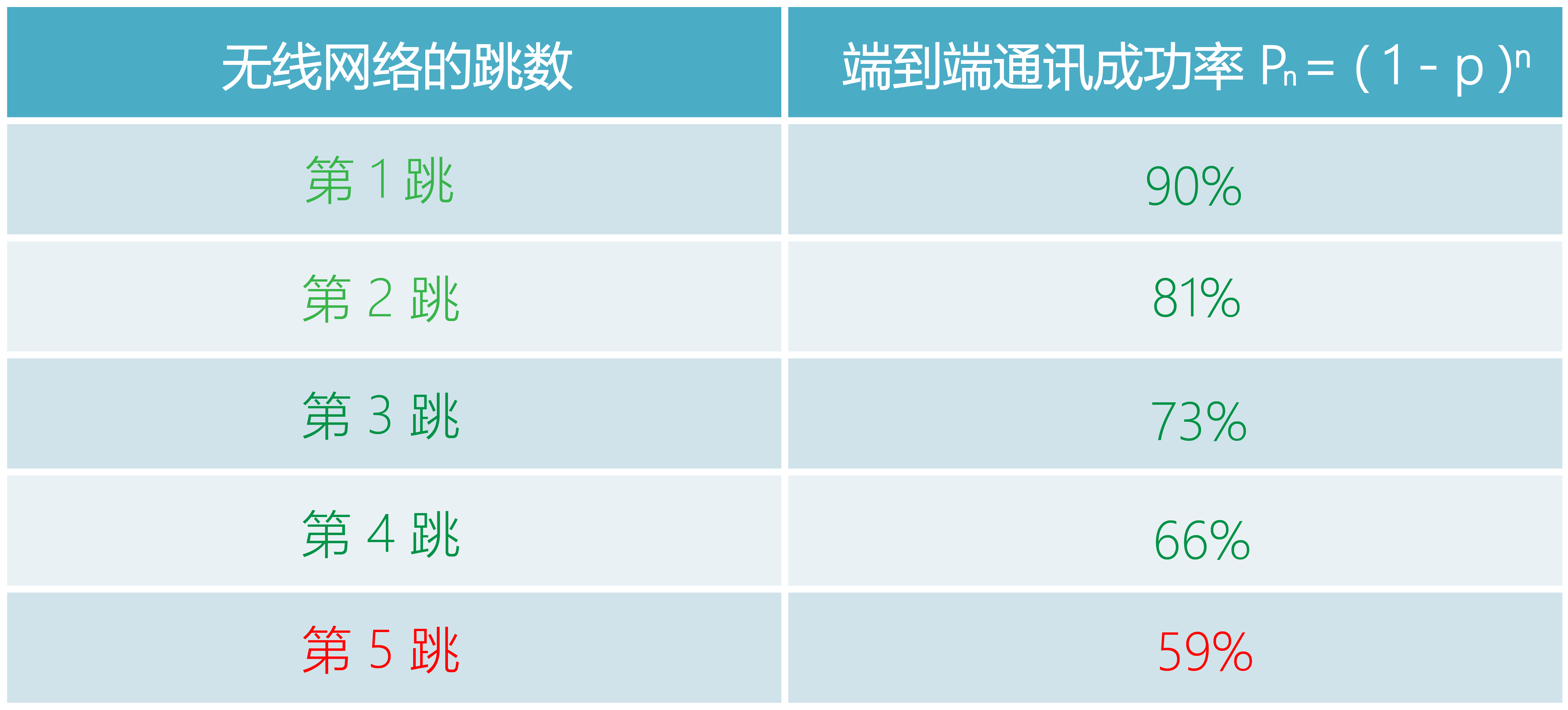
從上表我們看出，隨著網絡的跳數逐步增加，通訊成功率是明顯逐步降低的，到了第五跳 n=5，也就是第六個鏈路節點的時候，其成功率已經低于人們的心理“及格線”60%了。很多人在這種情況已經判定鏈路不穩定了。事實上有不少的工程師朋友在現場調試ZigBee網絡的時候，就發現了這個現象，但很少有人思考其背后的數學原理。

4、總結

通過上文的分析，我們可以看出，在室外長距離的無線自組織網絡中，由于節點之間的鏈路損耗較大，其鏈路預算相對不足，因此其包誤碼率PER會相應升高，也就是丟包概率 p會比較大；而在一個大規模網絡中，某些分支節點的通訊鏈路又會比較深，也就是網絡跳數 n比較大，在這種情況下其通訊成功率Pn自然也就顯著下降了，人們的切身感受就是這個鏈路不太穩定。

說到這里，有的讀者朋友心里可能會想，這還不簡單，給我上 TCP算法！加入端到端的數據重傳機制，那問題還不是立馬搞定？

效果果真如此么？請看后續文章分解！