前面講了整數槽繞組的磁勢,本期繼續講分數槽繞組的磁勢。
1. 分數槽繞組磁勢的特點
在介紹分數槽繞組磁勢之前,我們先復習一些數學基礎知識。
①關于傅立葉分解。根據傅立葉極數有關知識,一個滿足一定條件的周期函數可以分解為一個常數項和一系列不同周期(頻率)的三角函數(正弦、余弦函數)項之和,其中周期最長(頻率最低)的三角函數項的周期與被分解的函數周期相等,數學上常把這個周期最長(頻率最低)的三角函數項稱為基波;其余三角函數項的頻率都是基波頻率的整數倍,稱其為諧波。諧波頻率與基波頻率之比稱為諧波的次數,例如:諧波頻率與基波頻率之比為2的諧波稱為二次諧波;諧波頻率與基波頻率之比為3的諧波稱為三次諧波…。按照上述定義,諧波的次數均為整數。但是,在許多應用場合下,為了分析方便,而不將最低頻率項作為基波,而是將需要重點分析的頻率項作為基波,其余各項都作為諧波,這樣就會出現低于基波頻率的項,我們稱之為次諧波,而且還會出現諧波的次數不是整數的情況,即出現分數次諧波。實際應用中,用哪一個頻率作為基波頻率,取決于分析時關注的重點和分析的簡便性。由于電機主要依靠極對數為p的磁場實現機電能量轉換,因此將極對數為p的磁場波稱為工作波或稱主波,主波的波長為2τ。在分析電機的電磁性能時,常用主波作為基波,分析起來比較方便;而在分析振動噪聲時,常用一對極作為基波;在分析分數槽繞組的磁勢時,還常用一個單元電機的弧長作為基波的周期。這樣諧波的次數就不會出現次諧波和分數次諧波,使得計算更加簡便。
②關于諧波次數問題。我們曾在第一三一期——《電機繞組(8)》中講到,如果周期函數滿足f(x)=-f(x+T/2),即稱之為奇諧函數,奇諧函數做傅立葉分解時,只含有奇次諧波,而無偶次諧波;如果周期函數滿足f(x)=f(x+T/2),則稱之為偶諧函數,偶諧函數做傅立葉分解時,只含有偶次諧波,而無奇次諧波;如果周期函數不滿足以上兩種情況,則這種函數即不是奇諧函數,也不是偶諧函數,其做傅立葉分解時,就即含有奇次諧波,又含有偶次諧波。
了解了上述數學基礎知識,接下來我們就分析整數槽繞組與分數槽繞組磁勢的特點。
對于整數槽繞組,每極每相槽數q=整數,每對極下各相載流導體的安導波分布情況都是重復的,因而每對極下多相合成磁勢的波形也是重復的,且N極與S極下的磁勢大小相等、方向相反。也就是說,整數槽繞組的磁勢,在空間分布上是一個以2τ為波長(周期),極對數(頻率)為p的奇諧函數,將這樣一個周期函數作傅立葉分解,得到的最小頻率為p,如果將其定義為基波,即基波磁勢的波長為2τ,其他各項為諧波,則各諧波的次數均為整數,且諧波的次數僅存在奇次的高次諧波,而無偶次諧波。另外對于三相對稱繞組,其磁勢中也不包括三及三的整數次諧波。
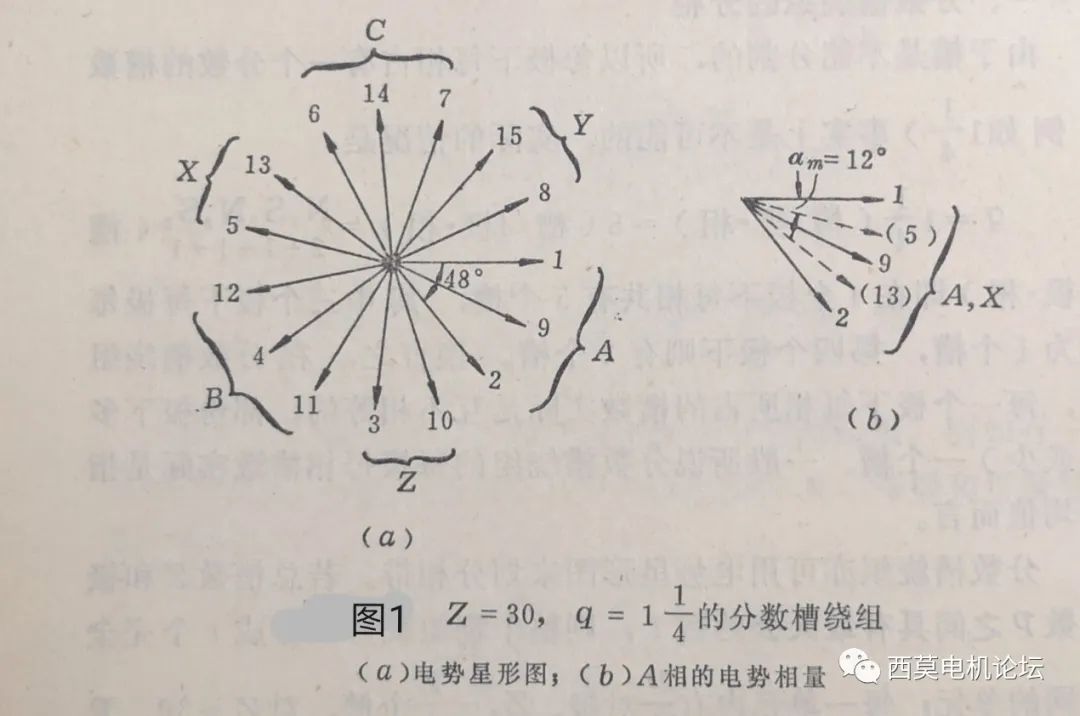
對于分數槽繞組,每極每相槽數q=b+c/d=N/d,為一不可約的分數,其中:N=b?d+c,稱其為分數槽繞組的每極每相等效槽數,N與d不可約。這就意味著每個極下分配給每相的槽數不是整數,而是d個極下每相才能得到整數N個槽,因此各個相帶內的極相組有大有小,相鄰兩對極下的安導波分布不相重復,只有經過一個單元電機后,安導波分布才重復一次,這就意味著分數槽繞組的磁勢是以一個單元電機的弧長為波長的周期函數,因此分數槽繞組的磁勢作傅立葉分解后,波長最大的一項其周期(波長)為一個單元電機的弧長,即最低頻率為單元電機的個數t,如果將其作為基波,其他項作為諧波,則諧波的次數就全部為整數,但此時基波的頻率并不是主波的極對數p,而是t,在這種定義下,主波變成了p/t次諧波;如果將主波作為基波,其他各項作為諧波,則諧波的次數就會出現分數次諧波和次數小于1的次諧波,而且諧波的次數還與q的分母d是偶數還是奇數有關。由此可見,與整數槽繞組相比,分數槽繞組的磁勢具有一系列的獨有的特點,其諧波含量要豐富得多,分析起來也更加復雜得多。下面先按照d是偶數還是奇數,分兩種情況說明分數槽繞組磁勢的諧波次數,然后再分析其幅值。
2. d為偶數時磁勢的諧波次數
若d為偶數,則每 d 個極就組成一個單元電機,所以每經過d個極,安導波及其所產生的磁勢波的波形將重復一次。將磁勢波進行傅立葉分解,若以單元電機在定子內圓所占弧長 d?τ作為基波波長,則磁勢的諧波次數 n′ 應為:
n′=1,2,3,4,5,6,… (1) 由于在一個周期d?τ范圍內,前半個周期(d/2)?τ內的安導波分布與后半個周期(d/2)?τ內的安導波分布即不滿足奇諧函數的條件,也不滿足偶諧函數的條件,也就是說,當d為偶數時,安導波即不是奇諧函數也不是偶諧函數,相應產生的磁勢同樣即不是奇諧函數也不是偶諧函數,因此磁勢的諧波中既有奇次諧波又有偶次諧波,但諧波次數 n′ 均為整數。由于主波波長為2τ,所以此時主波將成為d/2次諧波。
若改以主波作為基波,則其他各次諧波的次數υ就成為:
υ=n′/(d/2)=(2/d)?(1,2,3,4,5,6,…) (2) 此時υ既可能是整數,也可能是分數;既可能大于1,也可能小于1。換言之,用主波作為基波時,分數槽繞組的磁勢中既可能有高次諧波,也可能有低次和分數次諧波,次數低于主波(υ<1)的低次諧波,通常被稱為次諧波。
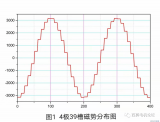
以一臺 Z1 =540槽、2p=48、 q=3+3/4的三相水輪發電機的定子繞組為例,該繞組的d=4。由于Z1與p之間具有最大公約數12,所以整個電機可以分成12個單元電機(即t=12),每個單元內有4極、45槽。圖1所示為定子 A 相電流達到最大值時,一個單元電機內三相合成磁勢的分布。
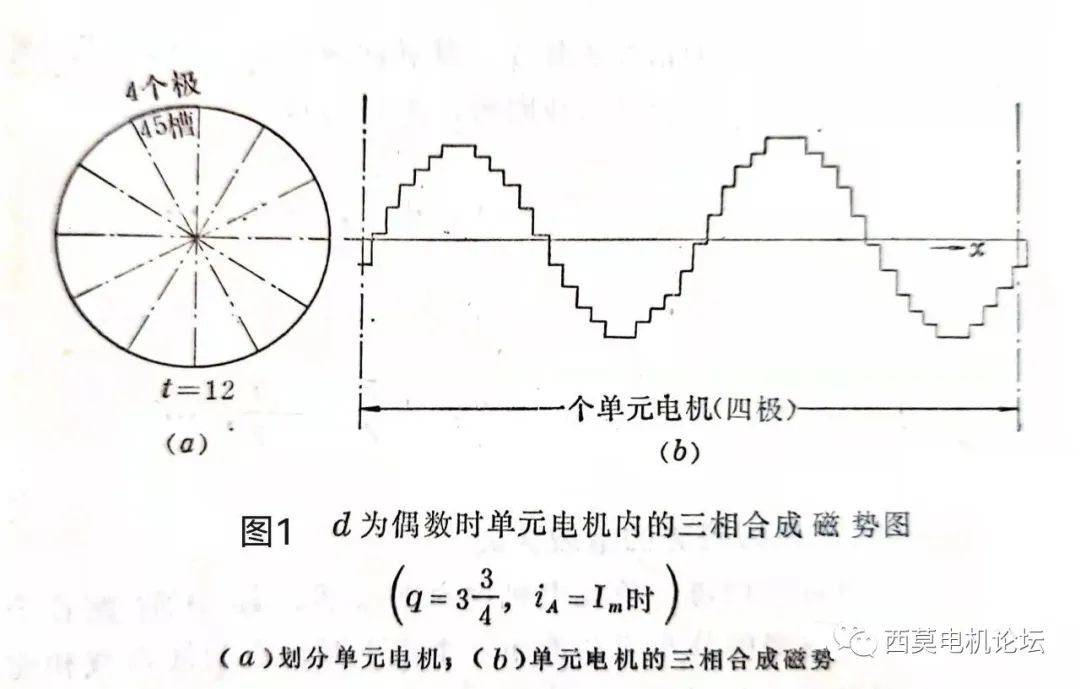 從圖1可知,每隔四個極,合成磁勢的分布波形將重復一次,故以4τ作為基波波長進行諧波分析時,諧波次數 n 應為:
從圖1可知,每隔四個極,合成磁勢的分布波形將重復一次,故以4τ作為基波波長進行諧波分析時,諧波次數 n 應為:
n′ =1,2,3,4,5,6,…
此時所有的諧波次數均為整數;對于波長為2τ的主波,此時將是二次諧波。
若以2τ作為基波波長,則主波成為基波,其他諧波的次數 υ 將成為:
υ=n′/(d/2)=(1/2)?(1,2,3,4,5,6,…)
=1/2, 1, 3/2, 2, 5/2, 3,…
此時將出現 υ 為1/2、3/2等分數次諧波。
以上是一般情況。若繞組為三相對稱,定子電流也是三相對稱,則合成磁勢中也不存在n′=3以及3的整數倍的諧波。若規定主波的轉向正,則與主波相鄰的其他諧波的轉向為正、反相間,于是就有:
n′=-1, +2, -4, +5,…
或:
υ=-1/2, +1, -2,+5/2, …
其中:n′=+2或υ=+1的諧波為主波;“+”表示該次諧波與主波轉向相同;“-”表示該次諧波與主波轉向相反。
3. d為奇數時磁勢的諧波次數
若 d =奇數,則每一單元電機內有2d個極,其中后面 d 個極下的安導波和磁勢波,應與前面 d 個極下對應點的安導波和磁勢波大小相等、方向相反,也就是說,d為奇數的分數槽繞組,其安導波和磁勢波均為奇諧函數。因此,用單元電機弧長2d?τ 作為基波波長來進行諧波分析時,磁勢波形中將僅含有奇次諧波,即:
n′=1,3,5,7,… (3) 此時主波的次數為d 。
若改以主波為基波,則諧波的次數 υ 將成為:
υ=n′/d=(1/d)?(1,3,5,7,…) (4) 同理,三相對稱運行時,不存在 n′=3及其倍數次的諧波。諧波磁勢的轉向,與 d =偶數時同樣確定。
以一臺 Z1 =456、2p=56、q =2+5/7的三相水輪發電機的定子繞組為例,該繞組的 d =7(奇數)。由于 Z1 與 p 之間具有最大公約數4,故整個電機可分為4個單元電機(即 t =4),每個單元電機有14個極,114槽。圖2表示 A 相電流達到最大值時,一個單元內的三相合成磁勢。
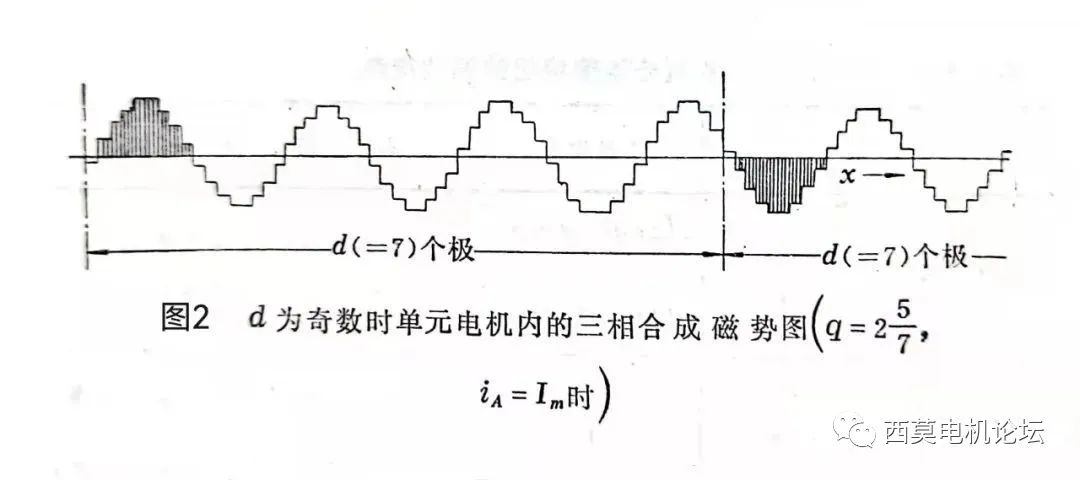
由圖2可見,后面7個極的磁勢波形與前面7個極的磁勢波形恰好反向,此時若以14τ作為基波波長來進行諧波分析,合成磁勢中將僅含有整數次的奇次諧波,即:
n′=+1,-5,+7,-11,+13,…
其中+7次諧波為主波。
若以主波作為基波,則諧波次數 υ 應為:
υ=n′/7=+1/7,-5/7,+1,-11/7,+13/7,…
即諧波次數將出現分數次。各次數前面的正負號所代表的意義同上。
4 用二極波作為基波時的諧波次數
通常情況下,都是把電機中的主波作為基波,即以2τ作為基波波長,這樣做對于研究整數槽繞組和發電機的電勢波形問題都非常方便。對于分數槽繞組,為避免把磁勢的諧波次數寫成分數形式,常以單元電機的弧長作為基波波長,此時主波成為 d(或d/2)次諧波。
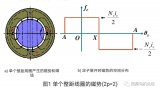
除了這兩種方式以外,諧波次數還有第三種表達方式。在分析振動和噪音問題時,常以整個電機的周長 πD 作為基波的波長,即以二極波作為基波。由于 πD=p?2τ,故采用此種方式表達時,主波就成為p次諧波。以六極電機(p=3)為例,電機中的主波為六極波。若以六極波作為基波,則主波即為基波(即υ=1);若以二極波作為基波,則主波成為三次諧波(即 n=3)。圖3用圖形表示了用主波或二極波表示時,諧波次數υ和n之間的關系。
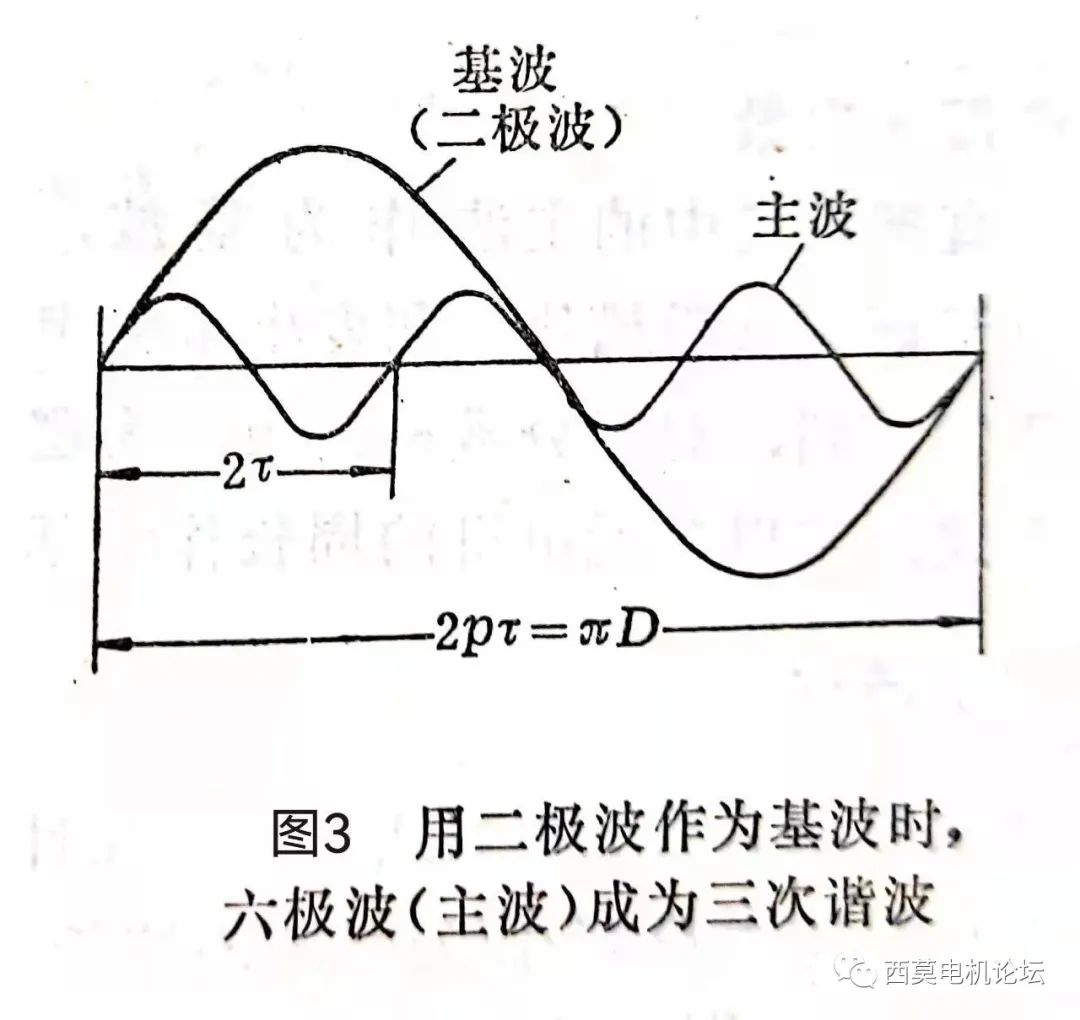 不難看出,用二極波表示時,諧波次數 n 應為:
不難看出,用二極波表示時,諧波次數 n 應為:
n=p?υ (5) 上述三種方式表達時,雙層分數槽繞組的諧波次數見表1。
 5 不同文獻中分數槽繞組磁勢諧波次數的計算公式
5 不同文獻中分數槽繞組磁勢諧波次數的計算公式
關于分數槽繞組磁勢諧波次數的描述和計算,在不同的文獻中有不同的分析方法和計算公式,上述介紹的計算方法與1983年水利電力出版社出版,由湯蘊璆、史乃、沈文豹所編的《電機理論與運行》中所述是一致的。為了便于同學們閱讀和理解不同文獻中關于分數槽繞組磁勢諧波的相關內容,現將收集到的各種文獻中關于分數槽繞組磁勢諧波的計算公式列于表2,并以實例對各文獻中公式的正確性予以驗證。
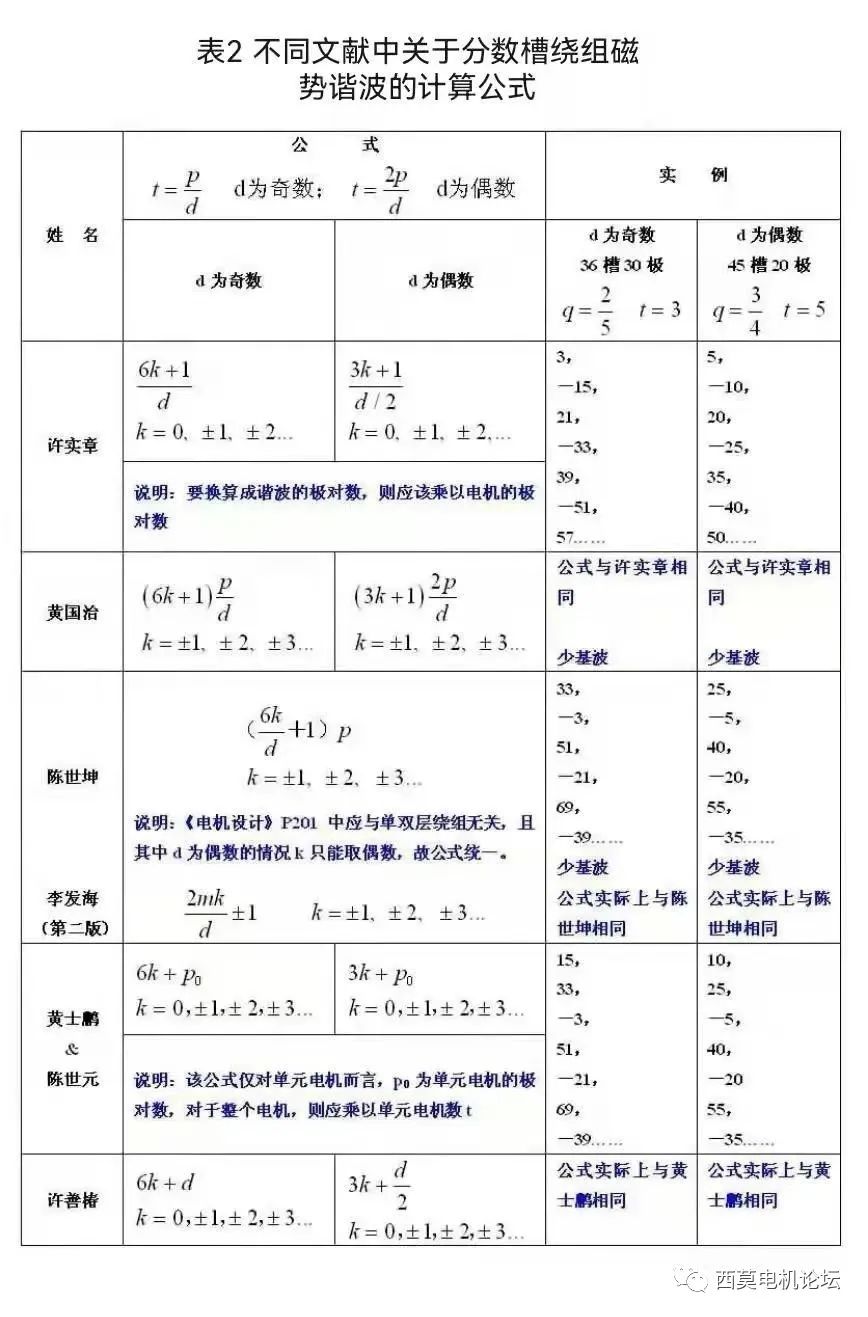
【注】表中文獻:許實章《交流電機繞組理論》;黃國治《Y2系列技術手冊》;陳世坤《電機設計》第2版;李發海等《電機學》第2版;黃士鵬、陳世元《交流電機繞組理論》;許善椿、金波交流電機定子分數槽繞組的諧波磁勢問題[J].大電機技術,1999,000 (003 ):1-5.。
通過分析和驗證,也發現某些文獻中的分析和描述存在一些錯誤,例如:陳世坤《電機設計》p201,就存在錯誤,分單雙層繞組進行討論,其實分數槽繞組的諧波次數與繞組的單、雙層是沒有關系的,而是跟q的分母是奇數還是偶數有關;此外黃士鵬、陳世元的《交流電機繞組理論》,里面對于分數槽的諧波極對數分析,其實僅對單元電機是正確的,對于非單元電機顯然還要乘以單元電機數t。
小結:各種文獻中雖然分析方法和計算公式不同,某些描述甚至存在一些小錯誤,但經過必要的修正后,基本上均是正確和一致的。其中許實章與黃國治兩位教授所著文獻中的公式基本相同,且與李發海等教授的文獻描述本質上是相同的;而其余三個文獻本質上也是相同的。
6. 定子磁動勢的幅值
與整數槽繞組相似,以主波作為基波時,分數槽繞組的三相基波合成磁動勢的幅值 F1 (安匝/極)應為:
F1=1.35?I?(Kdp1?W1)/p (6) 類似地,三相諧波合成磁動勢的幅值 Fυ為:
Fυ=(1/υ)?1.35?I?(Kdpυ?W1)/p (7) 式中:W1為定子每相串聯匝數;Kdp1為基波的繞組系數;Kdpυ 為 υ 次諧波的繞組系數。
與整數槽繞組相同,分數槽繞組的繞組系數也等于短距系數與分布系數的乘積,即Kdpυ=Kdυ?Kpυ,對于短距系數Kpυ,分數槽繞組與整數槽繞組的短距系數計算公式相同,即:Kpυ=sin[υ(Y1/τ)90o];而對于分布系數Kdυ,分數槽繞組的計算要比整數槽繞組復雜得多,對此,湯蘊璆教授早在1973年第3期的《大電機技術》上發表過一篇文章《分數槽繞組的分布系數》,在這篇文獻中有詳細的推導過程。這里推導過程略去,只講一下分數槽繞組分布系數的最終計算公式。
對于60相帶、具有“最大分布因數”的三相分數槽繞組,其各次磁勢諧波(包括基波υ=1)的分布系數為:
Kdυ=sin(N?αυ/2)/[N?sin(αυ/2)] (8) 式中:N為每極每相的等效槽數,N=b?d+c;角度αυ分兩種情況:
①當 d =偶數時:
αυ=D?d?αm?υ+180o(9) ②當 d =奇數時,又分兩種情況:
P為偶數時:
αυ=D?d?αm?υ(10) P為奇數時:
αυ=D?d?αm?υ+180o (11)
其中:αm=60o/N;D=(3N?P+1)/d;P為使D成為整數的最小整數。式⑻對任何次數(高次或低次、整數或分數次)的諧波都適用。
由以上各式可知,分數槽繞組的分布系數Kdυ除與諧波次數υ 有關外,還與每極每相槽數q 中的分母 d 以及 P 值的奇偶性有關。經過進一步推導,若僅考慮數值而不考慮正、負號時,式⑻可簡化為:
d=偶數時:
Kdυ=1/[2N?cos(D?n′?60o/N)] (12)
d=奇數且P=偶數時:
Kdυ=1/[2N?sin(D?n′?30o/N)] (13)
d=奇數且P=奇數時:
Kdυ=1/[2N?cos(D?n′?30o/N)] (14)
式中,n′為與υ相對應的諧波次數,見式⑵和式⑷:當d=偶數時,n′=υ?d/2;當d=奇數時,n′=υ?d 。
本期介紹了分數槽繞組的磁勢,與整數槽繞組相比,分數槽繞組的磁勢諧波更加豐富,除了有高次諧波外,還含有次數低于主波的次諧波和分數次諧波,在某些情況下,定子磁勢的次諧波與主極磁場相互作用,可使凸極同步電機的定子鐵心產生顯著的振動,在繞組設計時必須引起高度重視。
審核編輯:湯梓紅
-
電機
+關注
關注
142文章
9001瀏覽量
145337 -
諧波
+關注
關注
7文章
822瀏覽量
41779 -
函數
+關注
關注
3文章
4327瀏覽量
62573 -
繞組
+關注
關注
2文章
518瀏覽量
19867 -
同步電機
+關注
關注
2文章
257瀏覽量
25293
原文標題:電機繞組(十七)
文章出處:【微信號:西莫電機論壇,微信公眾號:西莫電機論壇】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
淺談三相繞組磁勢及其合成磁勢基波
多繞組反激變換器副邊電流峰值計算按照能量守恒還是磁勢守恒
電機基礎知識入門之交流繞組、電勢、磁勢等詳細資料免費下載
電機繞組:幾種不同形式的分數槽繞組對稱條件
三相電流不對稱時的繞組磁勢詳解
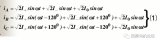




 分數槽繞組磁勢的特點
分數槽繞組磁勢的特點
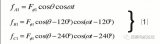










評論