在該系列的第八篇文章中，我們曾介紹過一階導數和二階導數對分析邊緣的結論：

一階導數通常在圖像中產生較粗的邊緣；

二階導數對精細細節，如細線、孤立點和噪聲有較強的響應；

二階導數在灰度斜坡和灰度臺階過渡處會產生雙邊緣響應；

二階導數的符號可用于確定邊緣的過渡是從亮到暗還是從暗到亮。

一階導數算子(例如 Sobel 算子)通過對圖像求導來確定圖像的邊緣，數值絕對值較高的點對應了圖像的邊緣。如果繼續求二階導，原先數值絕對值較高的點對應了過零點。因此，也可以通過找到二階導數的過零點來檢測邊緣。在某些情況下，找二階導數的過零點可能更容易。

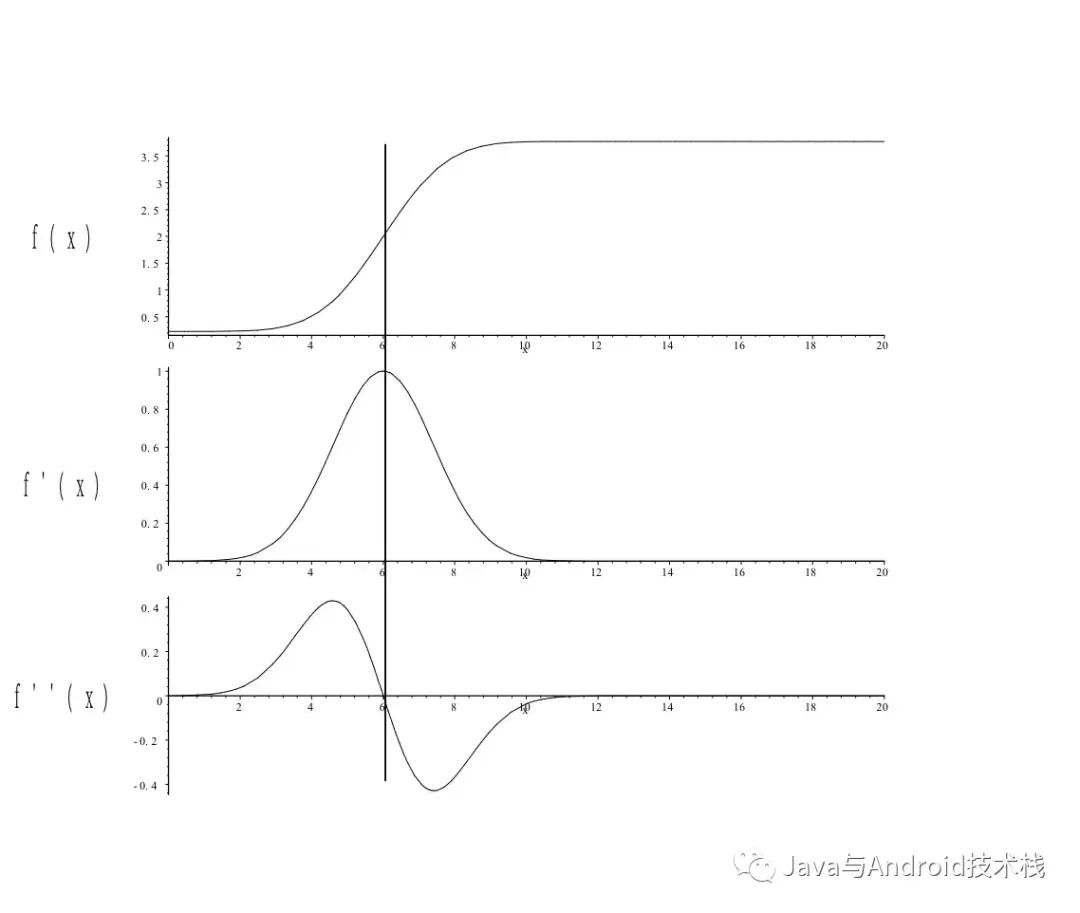
一階導數和二階導數.png

Part11. Laplace 算子

之前我們曾介紹過二階導數的 Laplace 算子可以通過差分近似來簡化，其公式為

它的卷積核：

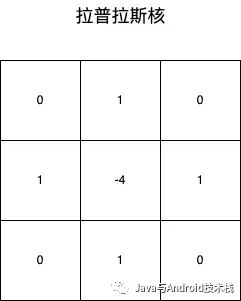
拉普拉斯核.png

這是它的 4 鄰域卷積核。

11.1 Laplace 算子的擴展

Laplace 算子是具有旋轉不變性的各向同性的算子。

將 4 鄰域的 Laplace 算子旋轉 45° 后，與原算子相加，就可以得到 8 鄰域的算子。

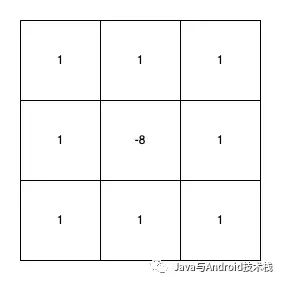
擴展的拉普拉斯算子.png

這是它的 8 鄰域卷積核。這個算子表示一個像素周圍一圈 8 個像素的和與中間像素 8 倍的差，作為拉普拉斯計算結果。

另外，還有兩個拉普拉斯卷積核，分別是對 4 鄰域卷積核和 8 鄰域卷積核取反。

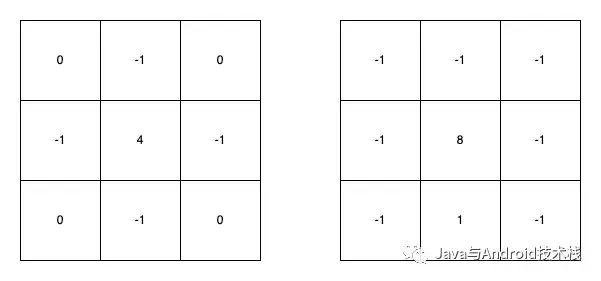
擴展的拉普拉斯算子2.png

21.2 圖像的模糊檢測

使用拉普拉斯變換對圖像進行模糊檢測的步驟大致如下：

對圖像進行拉普拉斯變換，檢測水平和垂直邊緣

然后對拉普拉斯變換后輸出的圖像求方差

如果圖像足夠清晰，輸出圖像的方差會大于給定閾值

如果圖像相對模糊，則拉普拉斯變換在圖像中并不能檢測到足夠的細節，邊緣就越少，從而導致輸出圖像的方差小于給定閾值

該過程需要選擇合適的閾值。

拉普拉斯算子能突出顯示圖像中包含快速梯度變化的區域，這些區域往往與邊緣有關。因此，如果一幅圖像的方差較高，說明圖像中存在廣泛的邊緣響應，包括類邊和非類邊，這是一幅正常聚焦圖像的代表。但如果方差很低，那么表明圖像中的邊緣響應很小，幾乎沒有邊緣存在。因此，通過比較方差與預設閾值的大小，可以判斷圖像是否模糊。

按照上面的步驟實現了一個模糊檢測的函數：

boolisImageBlurry(constchar*inputFile,doublethreshold)
{
Matsrc=imread(inputFile);
if(src.empty()){
printf("Imagenotloaded
");
returnfalse;
}

Matgray;
cvtColor(src,gray,COLOR_BGR2GRAY);
Matdst,absDst;
cv::Laplacian(gray,dst,CV_16S,3);
cv::convertScaleAbs(dst,absDst);

Matmean,stddev;
doublem=0,sd=0;
meanStdDev(absDst,mean,stddev);
m=mean.at(0,0);
sd=stddev.at(0,0);
doubleresult=sd*sd;
std::cout<

	

	然后寫一個程序來判斷一下這張圖是否是模糊的

	

	模糊的手機圖片.jpeg

	
intmain(intargc,char*argv[])
{
stringfileName=".../test.jpeg";
boolresult=isImageBlurry(fileName.c_str(),11.0);
cout<

	

	輸出結果：

	
m:2.5213
StdDev:6.31374
result=1


	

	說明是模糊的圖片。

	Laplace 算子對噪聲敏感，通常不適用于存在噪聲的圖像。

	Part22. LoG 算子

	LoG(Laplacian of Gaussian)邊緣檢測算子是 David Courtnay Marr 和 Ellen Hildreth 在 1980 年共同提出的，也稱為 Marr-Hildreth 算子，它根據圖像的信噪比來求檢測邊緣的最優濾波器。該算法先對圖像進行高斯平滑處理，然后再與 Laplacian 算子進行卷積。稍后來解釋為何是這樣的。

	先來回顧一下二維高斯函數的公式：

	

	高斯函數的一階導數和二階導數，在很多算子中都會用到。例如一階導數應用在 Canny 算子，二階導數應用在 LoG 算子等等。

	簡單推導一下它的一階導數：

	

	同理：

	

	還有推導一下它的二階導數：

	

	同理：

	

	將高斯函數代入拉普拉斯算子，可得 LoG 算子：

	

	Marr-Hildreth 算法如下：

	首先讓 LoG 核與一幅輸入圖像卷積：

	

	尋找 g(x,y) 的過零點來確定 f(x,y) 的邊緣位置。因為拉普拉斯變換和卷積都是線性運算，因此上式可以改成

	

	其中，f(x,y) 是輸入圖像，g(x,y) 是輸出圖像。

	這樣正好解釋了之前說的，該算法先對圖像進行高斯平滑處理，然后再與 Laplacian 算子進行卷積。因為先使用高斯濾波器對圖像進行平滑處理，可以減少噪聲和細節，然后使用拉普拉斯算子對濾波后的圖像進行邊緣檢測。

	它的優點是可以有效去除噪聲，同時保留圖像中的真實邊緣。相比 Laplace 算子，LoG 算子具有更好的邊緣定位能力和抗噪聲。但是它也存在一些缺點，計算量相對較大。

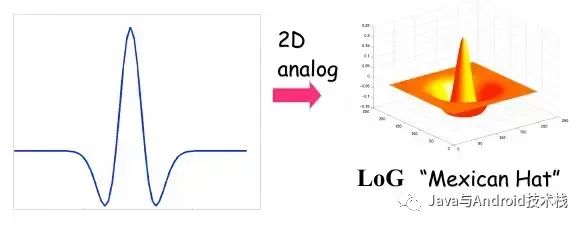
	下圖是負 LoG 算子的三維圖像，看上去很像“墨西哥草帽”。所以，在業界也被稱為墨西哥草帽小波(Mexican hat wavelet)。

	

	負 LoG 算子的三維圖像.png

	

	Mexican Hat.jpg

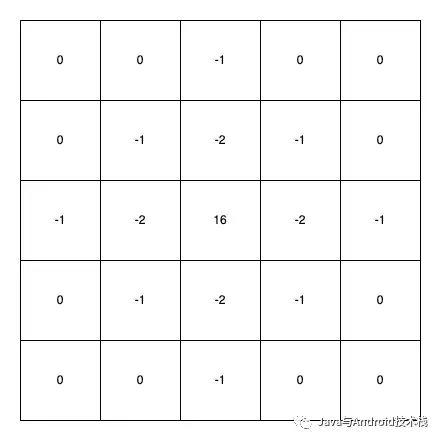
	負 LoG 算子可用 5*5 的模版近似表示

	

	LoG卷積核.png

	下面用高斯模糊和拉普拉斯變換來實現 LoG ：

	
intmain(intargc,char*argv[])
{
Matsrc=imread(".../street.jpg");
imshow("src",src);

Matdst,gray,edge;
cv::GaussianBlur(src,dst,cv::Size(3,3),0,0);//高斯模糊去除噪聲
cv::cvtColor(dst,gray,cv::COLOR_BGR2GRAY);//灰度化
cv::Laplacian(gray,edge,CV_16S,3);//使用拉普拉斯算子提取邊緣
cv::convertScaleAbs(edge,edge);

imshow("LoG",edge);

waitKey(0);
return0;
}


	

	

	Part33. 總結

	本文介紹了 Laplace 算子、LoG 算子，它們都是二階導數的邊緣算子。

	特別是 LoG 算子在 Laplace 算子的基礎上引入了高斯濾波，可以在一定程度上克服噪聲的影響。但它仍舊有一定的局限性，不過這種思想的引入對后續圖像特征研究起到了積極作用，被很多后續的算法所采納。

	

	審核編輯：湯梓紅