層間對齊度(Inter-layer alignment)是用于評估不同層次結構之間的相似性或一致性的指標。這一指標在許多應用中都是至關重要的,例如計算機視覺、自然語言處理、生物信息學等領域。本文將詳細介紹層間對齊度的計算方法,包括各種相關度量和算法。
一、介紹
在許多實際問題中,我們經常遇到不同層次結構之間的對齊問題。例如,在計算機視覺中,人們常常需要將圖像與對應的標注或語義分割結果進行對齊,以驗證模型的準確性。在自然語言處理中,對齊問題也非常常見,比如將句子與其對應的語義關系或語法分析結果進行對齊。
層間對齊度的計算方法主要包括以下幾種:
1.基于相似度的方法
基于相似度的方法是最常用的層間對齊度計算方法之一。它通過度量不同層次結構之間的相似性來評估它們的對齊程度。常見的相似度度量方法包括余弦相似度、歐氏距離、皮爾遜相關系數等。這些方法首先將不同層次結構表示為向量或矩陣,然后通過計算它們之間的相似性來計算對齊度。
2.基于圖匹配的方法
基于圖匹配的方法是一種更復雜的層間對齊度計算方法。它能夠處理更復雜的結構,比如圖形、樹等。此方法的關鍵思想是將不同層次結構表示為圖,并使用圖匹配算法來計算圖之間的相似性。常見的圖匹配算法包括最大子圖同構算法、圖編輯距離算法等。
3.基于信息論的方法
基于信息論的方法是一種較新的層間對齊度計算方法。它使用信息論中的概念和度量來評估不同層次結構之間的一致性。常見的信息論度量方法包括交叉熵、互信息、條件熵等。這些方法將不同層次結構表示為隨機變量,并使用信息論中的度量方法來計算它們之間的一致性。
4.基于機器學習的方法
基于機器學習的方法是一種更高級的層間對齊度計算方法。它通過將不同層次結構表示為特征向量,并使用機器學習算法來學習特征之間的聯系,從而計算對齊度。常見的機器學習算法包括支持向量機、隨機森林、神經網絡等。這些算法可以利用大量的訓練數據來學習特征之間的復雜關系,從而提高對齊度的準確性。
以上所述的方法只是層間對齊度計算中的一部分,實際上還存在其他很多方法。這些方法各有優劣,適用于不同的應用場景。在實際應用中,我們需要根據具體情況選擇合適的方法,以達到最好的層間對齊效果。
總結起來,層間對齊度的計算方法包括基于相似度的方法、基于圖匹配的方法、基于信息論的方法和基于機器學習的方法等。這些方法在不同的應用領域中發揮著重要的作用,幫助人們評估不同層次結構之間的對齊程度。在選擇具體方法時,我們需要考慮問題的復雜性、數據的特點以及計算資源等因素,以達到最佳的對齊結果。
-
神經網絡
+關注
關注
42文章
4814瀏覽量
104139 -
機器學習
+關注
關注
66文章
8510瀏覽量
134921 -
自然語言
+關注
關注
1文章
292瀏覽量
13697
發布評論請先 登錄
PCB多層板對準度控制設計 (英文)
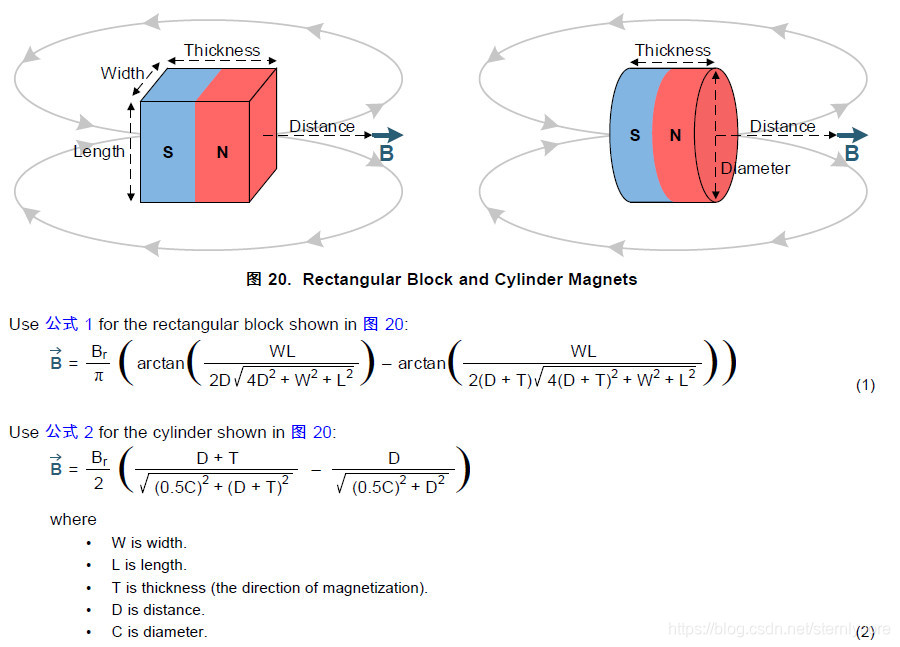
元件溫度的計算方法
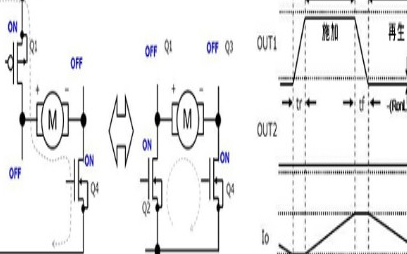
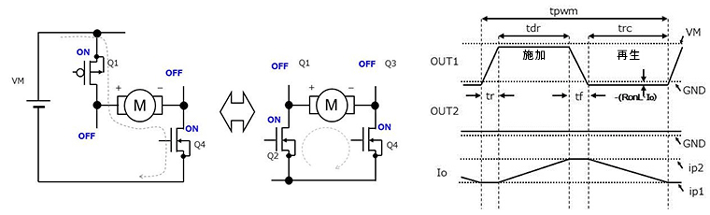
有刷電機驅動器的功耗計算方法(二)




















評論