許多同學問一個問題，電機繞組的感應電勢可以用Blv來計算，可是繞組的導體是嵌放在槽內的，而槽內的磁場B很小，幾乎為0，那么用Blv來計算時，將槽內這個很小的磁密代入其中，計算出線圈的感應電勢豈不是也很小，幾乎為0，這顯然與實際情況不符啊！是不是放在槽內的導體就不能用Blv的觀點來計算了？

其實這個問題我們在前面的瞎想文章——《電機繞組（七）》中已簡單地做了一些分析和說明，但并沒有從理論上進行詳細的論述和推導，既然大家對這個問題很感興趣，并且仍有許多疑問，那么本期就對這個問題進行一下詳細分析。

1 法拉第電磁感應定律

在分析槽內線圈的感應電勢之前，我們還是先復習一下法拉第電磁感應定律。法拉第電磁感應定律說的是，當匝鏈線圈的磁通φ發生變化時，線圈回路內就會產生感應電勢e。

e=-dφ/dt=-(d/dt)?【A】B?da (1)

式中：e的正方向與φ的正方向之間符合右手螺旋關系；A為積分區間，即線圈所包圍的面積；da為線圈所包圍面積上的面積微元；負號(-)表示感應電勢的實際方向符合楞次定律。

如果線圈的匝數為N，且磁通都與每匝線圈匝鏈，則整個線圈的感應電勢即為：

e=-N?dφ/dt (2)

需要說明的是，法拉第電磁感應感應定律給出了線圈的感應電勢與匝鏈線圈的磁通變化率之間的關系，說明感應電勢的大小只與磁通變化有關，與何種原因引起的磁通變化無關。根據法拉第電磁感應定律，無論什么原因導致磁通φ發生變化，只要匝鏈線圈的磁通發生變化，就必然會在線圈中產生感應電勢。而匝鏈線圈的磁通發生變化不外乎以下三種情況：一是線圈靜止不動，磁場B隨時間變化；二是磁場恒定(不隨時間變化)，但磁場與線圈之間發生相對運動，即人們常說的線圈做“切割磁力線”運動；三是上述兩種情況同時存在，既有切割磁力線運動，磁場也在隨時間變化。下面分別就這三種情況所產生的感應電勢作一詳細分析。

2 三種情況產生的感應電勢

2.1 線圈靜止而磁場隨時間變化時產生的感應電勢

將一個單匝線圈靜止放置于一個變化的磁場B中，即磁場B隨時間變化，是時間的函數，當然B還可能是空間位置的函數，也就是說，在不同的空間位置處磁場大小和方向可能不同，且隨時間變化，即B=f(x,y,z,t)，那么這個變化的磁場就會在單匝線圈中產生感應電勢。由此產生的感應電勢被稱為變壓器電勢，因為變壓器就是利用此原理工作的。根據法拉第電磁感應定律，這個變壓器電勢為：

eT=-dφ/dt |v=0=-(d/dt)?【A】B?da (3)

這里我們先埋下個小伏筆，線圈靜止而磁場發生變化的原因可能是多種多樣的，例如：可能是產生磁場的勵磁磁勢發生變化，從而導致磁場B發生變化；也可能是磁勢不變，而周圍的導磁介質發生了變化，從而導致磁場B發生變化。后面研究槽內線圈的感應電勢時就會遇到這種情況。

2.2 磁場恒定而線圈與磁場有相對運動時產生的感應電勢

將一個線圈置于一個恒定磁場B中，所謂恒定磁場是指該磁場B不隨時間變化，但可能在空間分布上不一定是勻強磁場，即磁密B只是空間位置的函數，并不隨時間變化。當線圈相對于磁場以速度v運動時，匝鏈線圈的磁通同樣會發生變化，從而產生感應電勢。由此產生的感應電勢被稱為運動電勢，這就是傳說中的“導體切割磁力線”產生的感應電勢，在旋轉電機中，這種感應電勢也被稱為旋轉電勢，用eM表示。

eM=∮【L】(v×B)?dl (4)

式中：L為積分區間，即線圈的周長；dl為線圈回路的線段微元(矢量)；v為運動速度矢量；B為磁密矢量。一定要注意⑷式中的各物理量都是矢量，式中的運算符號：“×”代表叉乘；“?”代表點乘。也就是說任意一段線圈微元dl切割磁力線產生的感應電勢等于該微元的運動速度矢量與該處磁密矢量的叉乘然后再與該微元矢量點乘，整個線圈回路的感應電勢等于每一小段線圈微元上的感應電勢在整個線圈回路周長上的積分。根據矢量運算的換算關系，(v×B)?dl =-B?(v×dl)，則⑷式可寫成：

eM=-∮【L】B?(v×dl) (5)

由于速度v=ds/dt，其中ds為在時間dt內線段dl在速度方向上的位移，所以v×dl=(ds/dt)×dl=dav/dt，其中dav表示在時間dt內dl所掃過的面積，如圖1所示。

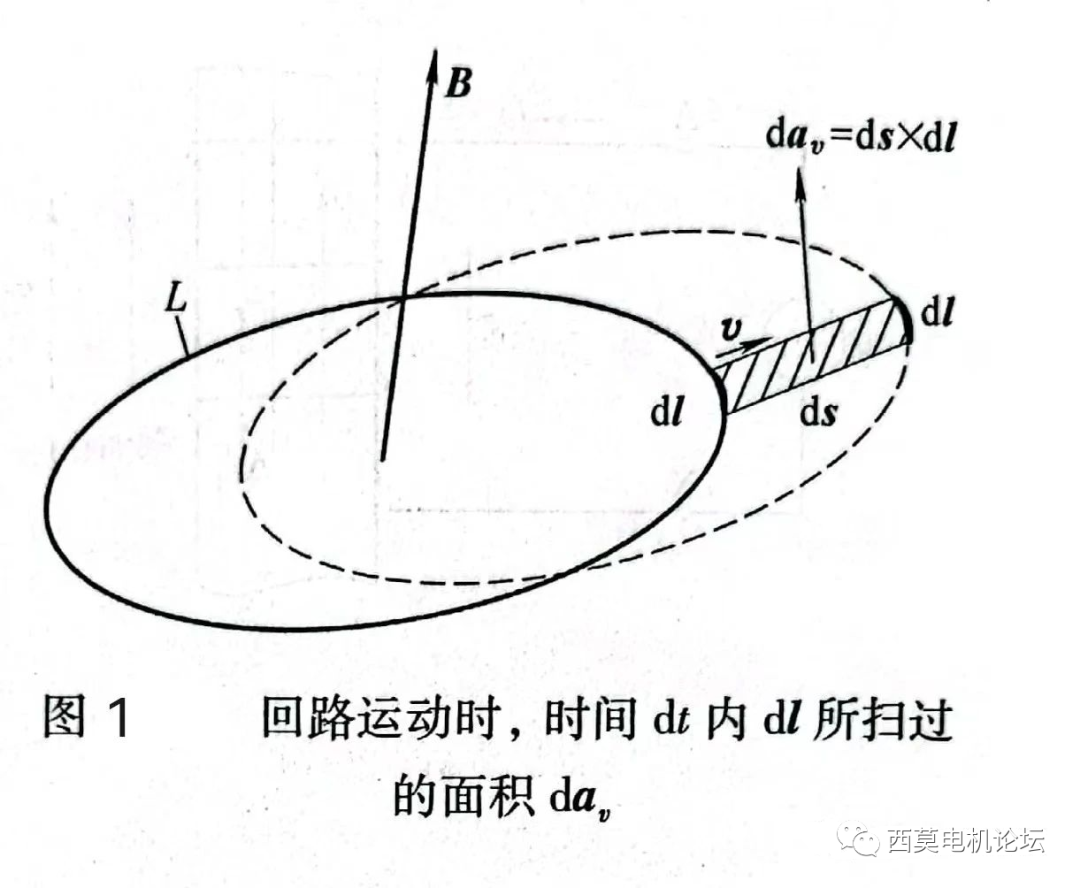
將上述v×dl=dav/dt代入⑸式得運動電勢：

eM=-∮【L】B?dav/dt=-dφv/dt (6)

式⑹表明，磁場恒定、線圈回路運動時，所產生的運動電勢eM就是線圈L所掃過的整個面積內的微分磁通量dφv隨時間變化率的負值，其中：dφv=∮【L】B?dav。

需要說明的是，上述推導是基于任意形狀的單匝線圈置于任意(大小、方向分布)恒定的磁場中，以任意(大小、方向)的速度運動而產生的運動電勢，因此上述各式和推導過程不失一般性，同學們可能看到這些公式和推導過程時有點懵圈，不要緊，其實電機中的具體情況并沒有那么復雜，只是上述普遍公式的一種特例。對于單根長直導線L，置于勻強磁場B中，以速度v做切割磁力線運動，在B、v、L三者互相垂直的情況下，導線在dt時間內掃過的面積為L?ds，其中ds為導線在dt時間內運動的位移，掃過該面積內的磁通微元為dφ=B?L?ds，該磁通除以時間dt，即為導體切割磁力線產生的運動電勢，即：

eM=dφ/dt=B?L?ds/dt=B?L?v (7)

這就是中學物理里說的導體切割磁力線產生的感應電動勢大小等于BLv，方向按右手定則判定。

2.3 既有磁場變化又有相對運動時產生的感應電勢

既有磁場變化又有相對運動是一種最為普遍的情況。如圖2所示，為一個單匝整距線圈處于一個正弦分布的脈振磁場中，且線圈置于光滑的轉子表面，隨轉子以機械角速度Ω作勻速旋轉為例，接下來我們就以此為例，計算一下線圈中的感應電勢。

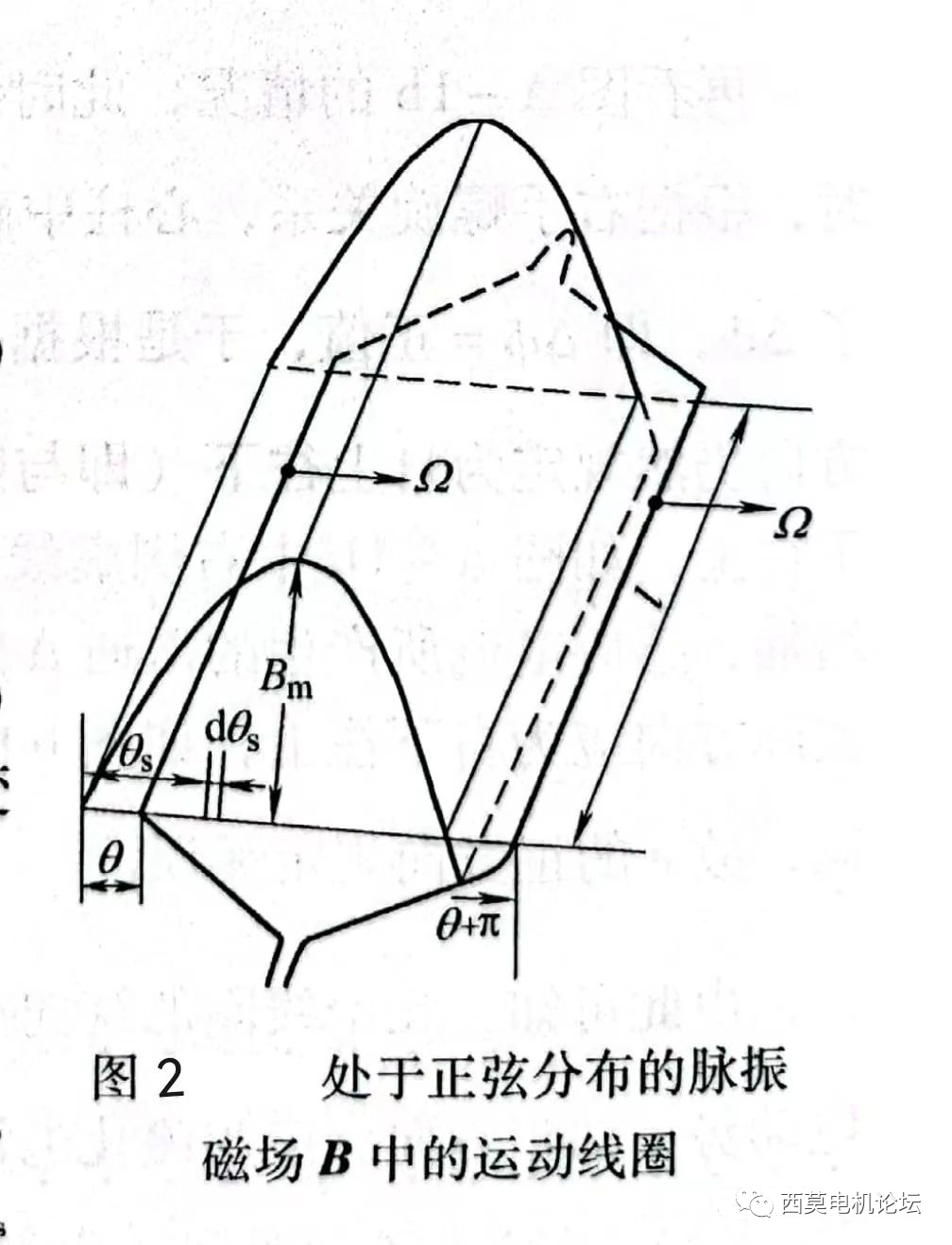
設氣隙磁場為一正弦分布的脈振磁場，B=Bm?cosωt?sinθs，θs為定子的電角度，先求匝鏈線圈的磁通：

φ=?【A】B?da=∫【θ,θ+π】Bm?cosωt?sinθs?l?(R/p)?dθs=Bm?cosωt?l?(R/p)?∫【θ,θ+π】sinθs?dθs(8)

式中：【A】為積分區間，即線圈在氣隙表面跨越的面積；R為氣隙的平均半徑；l為導體有效長度；p為極對數；積分下限為θ，上限為θ+π。由于線圈在運動，所以θ=pΩt=ωrt。于是按⑻式計算得：

φ=Bm?cosωt?l?(τ/π)?[cosθs]θθ+π=[Bm(2/π)τl]?cosωt?cosθ=φm?cosωt?cosθ (9)

式中：τ為極距；φm為氣隙磁通幅值，φm=(2/π)Bm?τ?l。

線圈中的感應電勢為：

e=-dφ/dt=-(d/dt)?[φm?cosωt?cospΩt]

=-[d(φm?cosωt)/dt]?cospΩt-[d(φm?cospΩt)/dt]?cosωt=eT+eM (10)

式中：eT和eM分別為變壓器電勢和運動電勢。

eT=-[d(φm?cosωt)/dt]?cospΩt=ωφm?sinωt?cospΩt (11)

eM=-[d(φm?cospΩt)/dt]?cosωt=pΩφm?sinpΩt?cosωt (12)

以上各式可知，變壓器電勢eT是由氣隙磁場隨時間交變引起，其大小取決于磁場B的交變頻率ω和磁通幅值φm；運動電勢eM則是由線圈運動引起，其大小取決于旋轉角速度Ω和磁通幅值φm(或者說2Bm?l?v)。

3 應用法拉第定律時需要注意的事項

應用法拉第定律時，有幾點需要注意：

①感應電動勢中，運動電動勢eM和變圧由動墊eT的劃分，與觀測的坐標系有關，坐標系的速度不同，觀測到的eM和eT值就不同，但是總的感應電勢值是不變的，與坐標系的速度無關。例如在計算同步電機定子(電樞)繞組的空載感應電動勢時，如果把坐標系放在旋轉的主極上，由于主極磁場 Bf 為恒定不變，故定子導體內的感應電動勢，可以認為是導體對主極反向旋轉所產生的運動電動勢 eM，此時 eM可用 Blv 法計算；但是，如果把坐標系放在定子上，則定子繞組內的感應電動勢，就應看成是繞組內的磁通量隨時間而變化所產生的變壓器電勢 eT。不難得知，兩者算出的值是相同的。

②在計算運動電勢時，周圍的磁介質應為均勻或者保持不變。如果磁介質有所變化，則由于磁介質的變化將引起磁場發生變化，從而產生變壓器電動勢。這就是我們前面所說埋下的伏筆，在接下來研究電樞開槽、線圈置于槽內時，線圈的電動勢時將會遇到這種情況。

③在計算電勢時，常常要涉及磁場 B 的分布和變化。為形象化起見，工程上常常用磁力線來描述磁場的分布。對于大多數問題，這樣做有助于理解，并能得到正確的結果。但是磁力線不是物理的實體，而僅是一種數學上的描述手段。因此決不能把磁力線“物質化”，把它當作物質的“線”或者“橡皮筋”等，當主磁極發生平移或旋轉運動時，誤認為磁力線跟著磁極一起移動，從而對某些問題作出錯誤的判斷和結論，這點應當注意。

4 槽內線圈的感應電勢

在惡補完以上基礎知識后，接下來我們就言歸正傳，正式講解電樞開槽，線圈置于槽內時，匝鏈線圈的磁通變化情況和產生的感應電勢。

以直流電機為例，設定子主機磁場恒定，電樞以轉速n旋轉。

4.1 線圈置于光滑電樞表面時的感應電勢

如圖3所示，一個單匝整距線圈置于光滑的電樞表面，線圈由導體1和導體2構成，它們分別位于主極的N極和S極下，該處磁密大小為B。

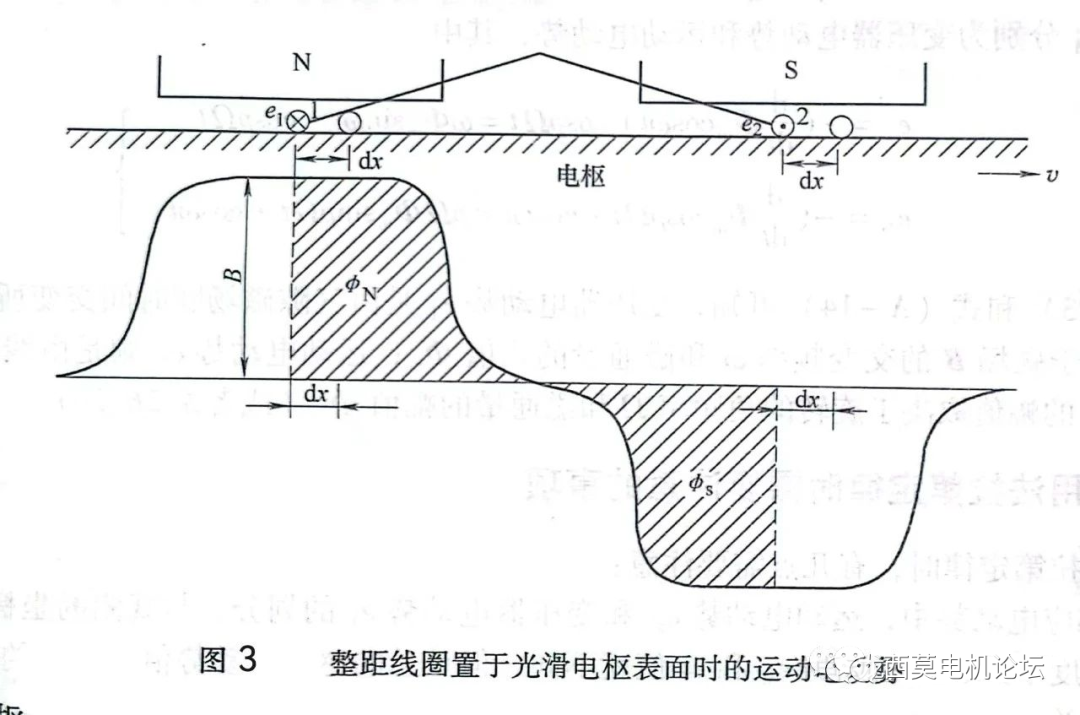
設電樞旋轉時，導體1和導體2以線速度v在主極磁場內作切割磁力線運動，按照“Blv觀點”，兩根導體的運動電勢e1和e2分別為：

e1=Blv；e2=-Blv (13)

其中 l為導體有效長度。整個線圈的感應電勢為：

e=e1-e2=2Blv (14)

從另一個角度來看，按照“dφ/dt觀點”，在時間dt內，導體移過的距離為dx，在磁場內掃過的面積為l?dx，線圈所包圍的N極下的磁通量φN將逐步減少，S極下的磁通量φS將逐步增加，匝鏈整個線圈的磁通量變化為：

dφN=-Bldx；dφS=-Bldx (15)

于是線圈的感應電勢為：

e=-(dφN+dφS)/dt=2Bldx/dt=2Blv (16)

由(14)、(16)式可見，在導體置于光滑電樞表面時，無論用“Blv觀點”還是用“dφ/dt觀點”計算，所得到的結果是一致的。

4.2 電樞表面開槽、線圈置于槽內時的感應電勢

如圖4所示為電樞表面開槽、一個單匝整距線圈置于槽內的情況，開槽后由于槽口處的氣隙增大，磁阻增大，故該處的氣隙磁密將顯著減弱，從B下降為b，使氣隙磁密的分布在該處有一明顯的凹坑。現在的問題是，若轉子和槽內線圈仍以線速度v運動，線圈的感應電勢是否也會減小？

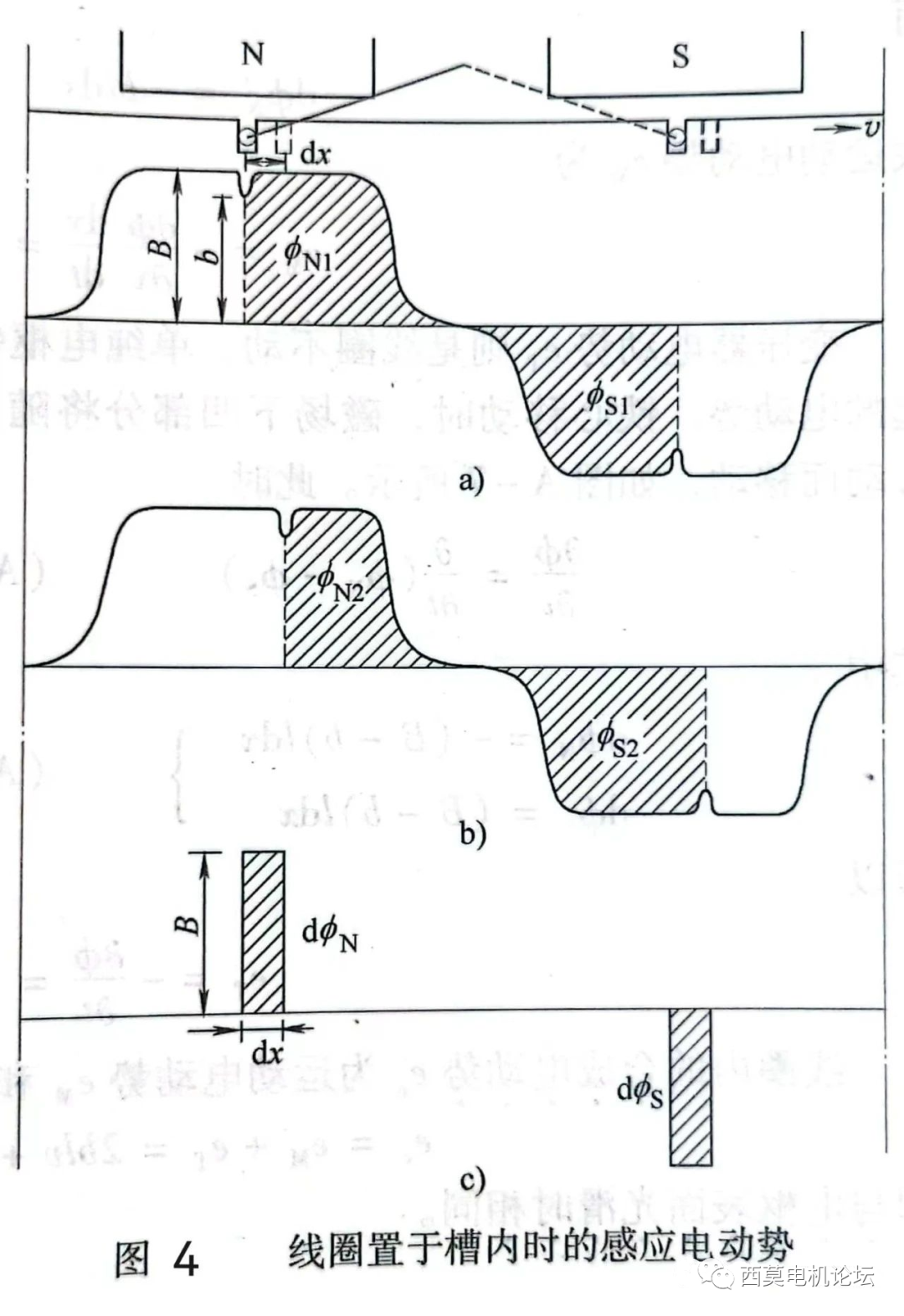
我們先用“dφ/dt觀點”來計算。設一開始兩導體分別處于N極和S極的正下方，如圖4a)所示的實線槽位置，線圈所匝鏈的N極和S極下的磁通量分別為圖4a)中的陰影面積φN1和φS1，匝鏈線圈的總磁通為：

φ1=φN1-φS1(17)

由于線圈和鐵心一起運動，經過時間dt后，線圈及其所在的槽均向右移動了dx距離，移至圖4a)所示的虛線位置，則此時線圈所匝鏈的N極和S極下的磁通量分別分別變成了圖4b)中的陰影面積φN2和φS2，匝鏈線圈的總磁通變為：

φ2=φN2-φS2(18)

也就是說，經過時間dt后，匝鏈線圈的磁通的變化量為：

dφ=φ2-φ1=(φN2-φS2)-(φN1-φS1)=(φN2-φN1)-(φS2-φS1)=dφN-dφS (19)

式中：

dφN=φN2-φN1=-Bldx (20)

dφS=φS2-φS1=Bldx (21)

分別表示經過時間dt后，線圈匝鏈N極下的磁通變化量和S極下的磁通變化量，分別對比圖4a)和圖4b)中N極下和S極下的兩塊陰影面積的變化，不難看出，N極下匝鏈的磁通從φN1變化到φN2，陰影面積減小了，兩塊陰影面積的減小量與凹坑處的磁密b無關，只與非凹坑處的磁密B有關；同理S極下的磁通變化也是只與與非凹坑處的磁密B有關，如圖4c)所示。這個結論從(20)式和(21)式中也可看出。將(20)、(21)兩式代入(19)式得：

dφ=-2Bldx (22)

線圈中的感應電勢為：

e=-dφ/dt=2Bldx/dt=2Blv (23)

由(23)式可見，開槽后，槽內線圈的感應電勢與開槽前(光滑電樞表面時)是相同的，也就是說，電樞開槽與否并不影響線圈感應電勢的大小，開槽后仍可用“Blv”計算線圈感應電勢，其中的磁密必須是開槽前的氣隙磁密B，而不是槽內的磁密b！以上是用普遍適用的法拉第電磁感應定律推導出的槽內線圈感應的結論，接下來我們進一步分析這個結論的原因。

電樞開槽后，線圈的感應電勢中實際上包含了運動電勢和變壓器電勢兩個分量，即：

e=-dφ/dt=-[?φ/?t+(?φ/?x)?dx/dt]=eT+eM(24)

其中： eT=-?φ/?t，為變壓器電勢；eM=-(?φ/?x)?dx/dt，為運動電勢。

先說運動電勢。運動電勢eM是指鐵心(槽)不動，僅有線圈在槽內做切割磁力線運動時產生的電勢。設在時間dt內線圈在槽內移動了dx距離，如圖5所示。

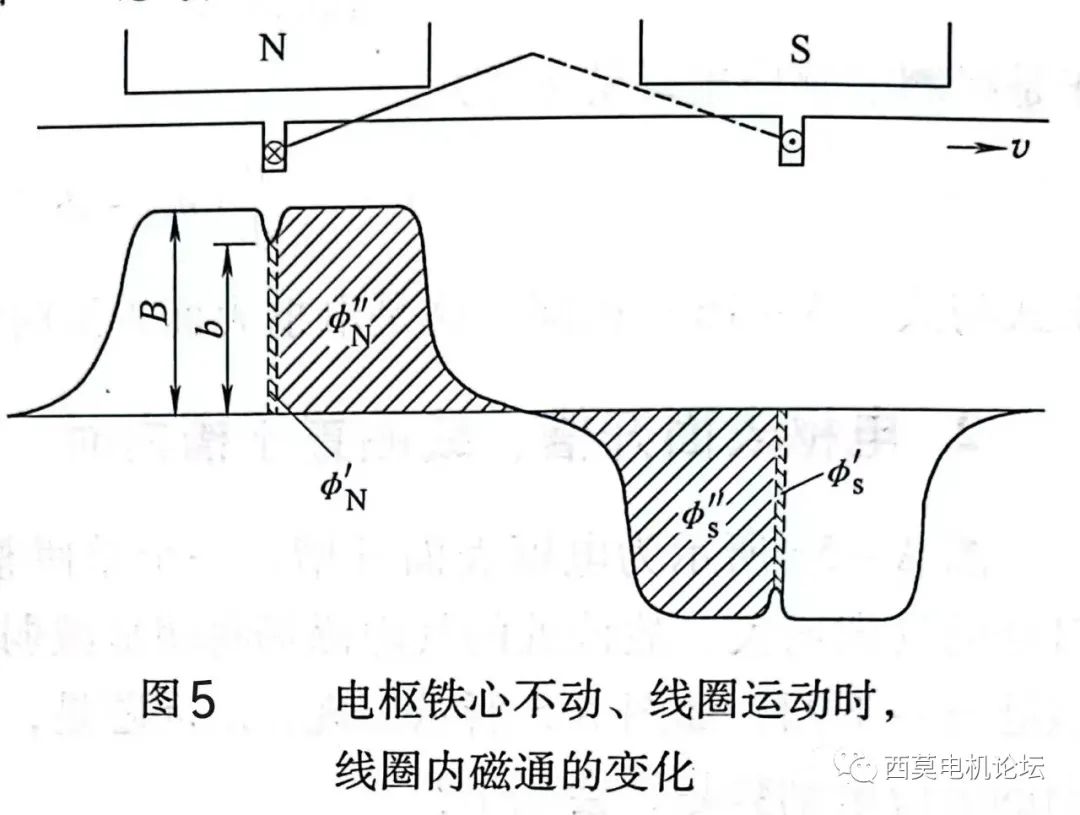
把φN和φS各分成φN′、φN″和φS′、φS″兩部分，則：

?φ/?x=(?/?x)[(φN′+φN″)-(φS′+φS″)] (25)

線圈在槽內發生位移，只有φN′和φS′發生變化，φN″和φS″并不變化(即dφN″=dφS″=0)，于是：

?φ/?x=?φN′/?x-?φS′/?x (26)

而dφN′=-bldx；dφS′=bldx，故運動電勢eM即為：

eM=-(?φ/?x)?dx/dt=2bldx/dt=2blv (27)

式(27)表明，運動電勢分量等于采用“BLv觀點”計算的運動電勢，但此時的磁密應該用槽內磁密b來計算，這樣計算出的感應電勢的確是顯著減小了。但這只是線圈感應電勢中的運動電勢分量，全部感應電勢中還有另一個分量——變壓器電勢。

再說變壓器電勢。這里的變壓器電勢則是指：線圈不動、單純電樞鐵心(槽)移動，由于線圈周圍的磁介質分布發生變化，使得匝鏈線圈的磁通量發生變化，從而引起的感應電勢。鐵心移動時，磁場的凹坑將隨槽的移動而移動，如圖6所示。

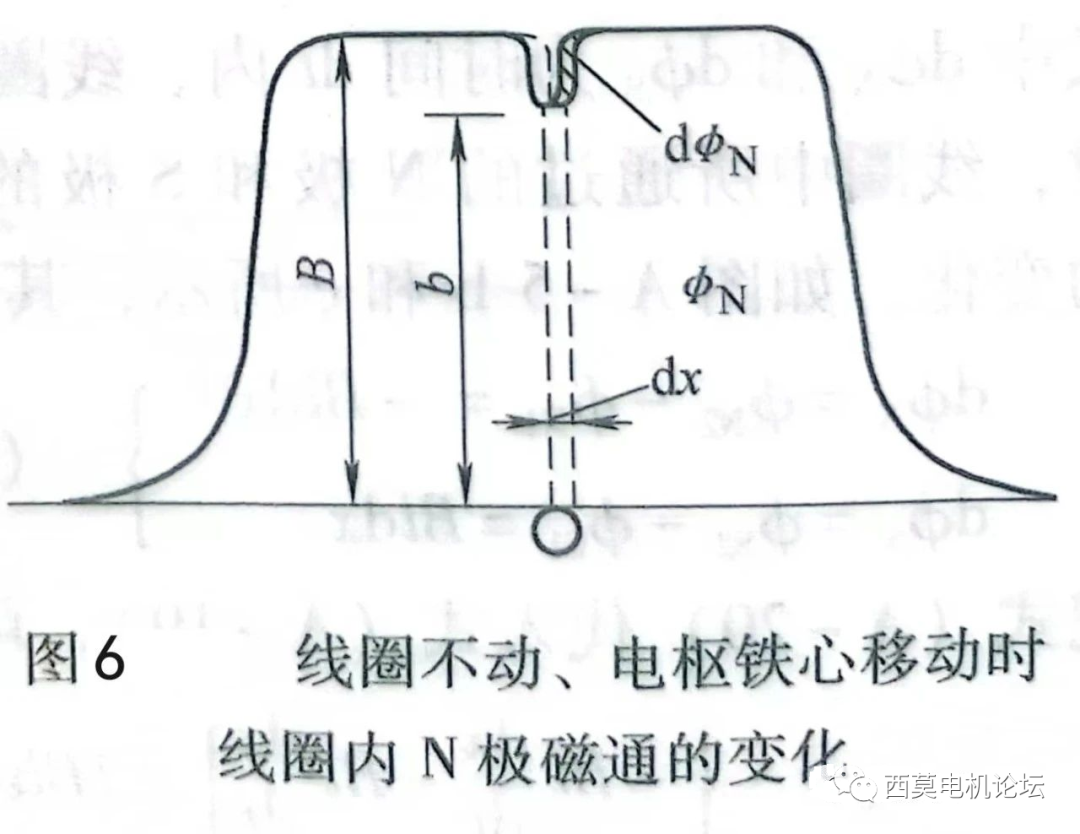
此時：

?φ/?t=? (φN-φS)/?t (28)

其中：

dφN=-(B-b)ldx (29)

dφS=(B-b)ldx (30)

因此，變壓器電勢：

eT=-?φ/?t=2(B-b)lv (31)

線圈內總的感應電勢為：

e=eT+eM=2(B-b)lv+2blv =2Blv (32)

由(27)、(31)和(32)式可知，開槽后雖然運動電勢2blv是顯著減小了，但減小的部分卻用變壓器電勢2(B-b)lv又找補回來了，即開槽后線圈總的感應電勢與電樞光滑時是相同的，在計算開槽后槽內線圈的感應電勢時，同樣可以用“Blv觀點”來計算，其中的磁密還用不開槽時的氣隙磁密值B代入。

審核編輯：湯梓紅