支持向量機(Support Vector Machine,簡稱SVM)是一種非常流行和強大的機器學習算法,常用于分類和回歸問題。它的基本原理源自于統計學和線性代數的理論基礎,通過找到能夠在特征空間中劃分不同類別的最優超平面,從而實現對數據的準確分類。
SVM的基本原理可以通過以下幾個關鍵概念來解釋和理解。
1.間隔和邊界:SVM的目標是找到一個超平面,能夠將不同類別的樣本數據分開,并且使得間隔最大化。間隔是指超平面與兩個最近的樣本點之間的距離,而邊界是指超平面兩側的樣本點構成的區域。通過最大化間隔,可以提高分類器的魯棒性和泛化能力。
2.支持向量:在SVM中,只有位于邊界上的樣本點才對分類決策起作用,這些樣本點被稱為支持向量。支持向量是決定超平面位置的關鍵因素,因為它們確定了分類邊界的位置和姿態。
3.核函數:對于非線性可分的數據,SVM引入了核函數的概念。核函數能夠將原始的特征空間映射到一個更高維度的特征空間,使得原本線性不可分的樣本在該高維空間中線性可分。常見的核函數有線性核、多項式核、高斯核等。
SVM可以解決許多機器學習問題,包括但不限于以下幾個方面。
1.二分類問題:SVM最常見的應用是解決二分類問題,即將給定的樣本數據分為兩個類別。通過找到一個超平面,SVM能夠在特征空間中將兩個類別的樣本點分隔開。
2.多分類問題:SVM也可以通過一對多(One-vs-All)的策略來解決多分類問題。這種方法將多個二分類問題組合在一起,具有高效和簡單的優勢。
3.回歸問題:除了分類問題,SVM還可以用于回歸問題。與傳統的線性回歸方法不同,SVM回歸能夠通過間隔損失函數來適應非線性關系,預測連續數值變量。
4.異常檢測:SVM的間隔最大化能力使其非常適合于異常檢測問題。通過訓練一個SVM分類器,可以將正常樣本和異常樣本區分開來,從而實現異常點的識別。
5.特征選擇:SVM能夠根據樣本點的重要性自動選擇特征,通過優化間隔最大化來達到高效的特征選擇,降低維度。
雖然SVM在很多問題上具有廣泛應用,但也存在一些限制。主要的局限性包括數據集規模較大時計算復雜度較高、核函數的選擇和參數調優等。
總結起來,支持向量機是一種基于間隔最大化原則的機器學習算法,可用于解決二分類、多分類、回歸和異常檢測等問題。憑借其魯棒性、泛化能力和特征選擇等優勢,SVM在實踐中得到廣泛應用。
-
函數
+關注
關注
3文章
4327瀏覽量
62573 -
支持向量機
+關注
關注
0文章
71瀏覽量
12715 -
機器學習
+關注
關注
66文章
8406瀏覽量
132566 -
數據集
+關注
關注
4文章
1208瀏覽量
24689
發布評論請先 登錄
相關推薦
基于支持向量機的預測函數控制
基于改進支持向量機的貨幣識別研究
基于支持向量機(SVM)的工業過程辨識
多分類孿生支持向量機研究進展
支持向量機的故障預測模型
什么是支持向量機 什么是支持向量
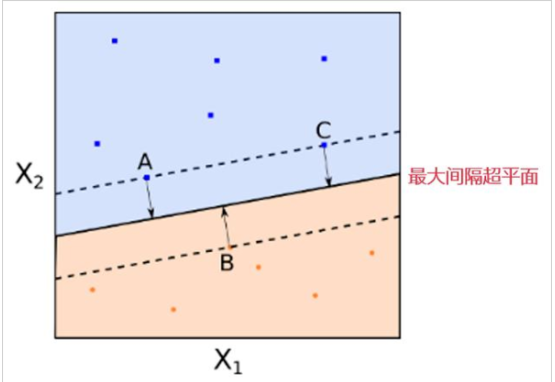




 支持向量機的基本原理 支持向量機可以解決什么問題
支持向量機的基本原理 支持向量機可以解決什么問題
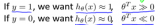











評論