哈夫曼編碼是一種基于頻率的變長編碼方式，常用于數(shù)據(jù)壓縮和信息傳輸領域。它是由美國數(shù)學家大衛(wèi)·哈夫曼在1952年發(fā)明的，被廣泛應用于無損壓縮領域。

哈夫曼編碼算法的基本思想是根據(jù)字符出現(xiàn)的頻率構建一棵二叉樹，將出現(xiàn)頻率高的字符用較短的編碼表示，而出現(xiàn)頻率低的字符則用較長的編碼表示。通過這種方式，可以實現(xiàn)對數(shù)據(jù)進行高效的編碼和解碼。

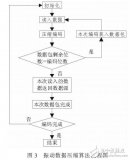
下面我們將詳細介紹哈夫曼編碼的算法過程。

1. 統(tǒng)計字符頻率
   在進行哈夫曼編碼前，首先需要統(tǒng)計字符出現(xiàn)的頻率。這可以通過遍歷待編碼文本，計算每個字符的出現(xiàn)次數(shù)來實現(xiàn)。
2. 構建哈夫曼樹
   根據(jù)字符的頻率，我們可以構建一棵哈夫曼樹，其中每個葉子節(jié)點代表一個字符，節(jié)點的權重為字符的頻率。構建哈夫曼樹的過程可以采用貪心算法，即每次選擇權重最小的兩個節(jié)點合并，直到所有節(jié)點都合并為一棵樹。
3. 為每個字符分配編碼
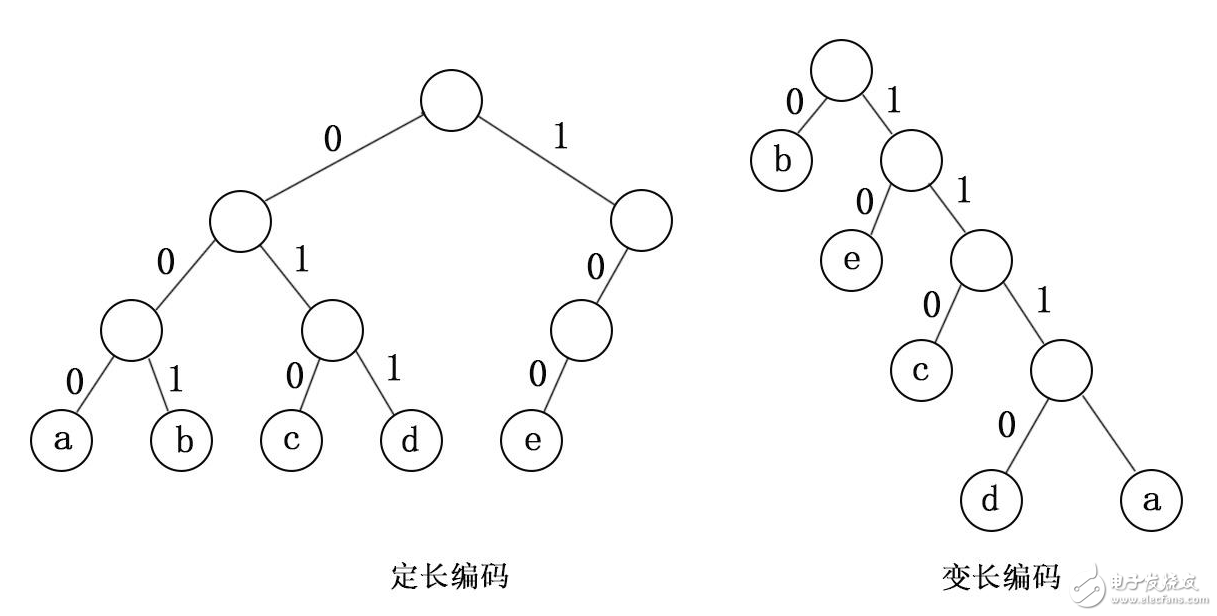
   在哈夫曼樹構建完成后，需要為每個字符分配唯一的編碼。從根節(jié)點出發(fā)，對于每個左子樹，分配編碼為0，對于每個右子樹，分配編碼為1。經過哈夫曼樹的路徑，即可得到每個字符對應的編碼。
4. 編碼與解碼
   根據(jù)某字符串，將每個字符替換為其對應哈夫曼編碼，即可實現(xiàn)編碼過程。而在解碼時，通過從哈夫曼樹的根節(jié)點開始，根據(jù)每個0或1依次向下遍歷哈夫曼樹，直到到達葉子節(jié)點，即可得到原始數(shù)據(jù)。

接下來，我們來詳細介紹哈夫曼編碼的左邊是0還是1的問題。

在構建哈夫曼樹時，我們需要通過貪心算法合并權重最小的兩個節(jié)點。合并時，我們通常將權重較小的節(jié)點放在樹的左邊，而權重較大的節(jié)點放在右邊。這是因為0通常表示左子樹，1通常表示右子樹。在遞歸地構建哈夫曼樹時，每次合并的兩個節(jié)點一定是樹中權重最小的兩個節(jié)點，因此，合并生成的節(jié)點通常都是左子樹。而右子樹則是原本樹中權重次小的節(jié)點。

因此，在哈夫曼編碼中，通常將左子樹表示為0，右子樹表示為1。這種方式可以確保每個字符的編碼是唯一的，并且可以通過編碼快速定位到對應的字符。

總結起來，哈夫曼編碼是一種通過構建哈夫曼樹實現(xiàn)的基于頻率的變長編碼方式。在構建過程中，通常將左子樹表示為0，右子樹表示為1。該編碼方式可以高效地實現(xiàn)數(shù)據(jù)的壓縮和解壓縮，并被廣泛應用于數(shù)據(jù)壓縮和信息傳輸領域中。