線性反饋移位寄存器(Linear Feedback Shift Register, LFSR)是一種重要的序列發生器,廣泛應用于密碼學、通信和數值計算領域。在本文中,我們將詳細介紹線性反饋移位寄存器的工作原理、輸出序列的計算方法以及其在不同領域中的應用。
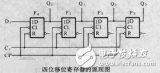
首先,我們來了解線性反饋移位寄存器的基本結構和工作原理。LFSR是一種特殊的移位寄存器,由多個觸發器和異或門組成。觸發器用于存儲和傳輸二進制位,異或門用于實現線性反饋。LFSR的位數決定了它所能生成的最長周期,而反饋連接決定了它所產生的序列。LFSR利用反饋循環和位移操作,不斷更新內部狀態,從而產生復雜的偽隨機序列。
在開始計算LFSR的輸出序列之前,我們需要確定以下幾個參數:初始狀態、反饋多項式和位數。初始狀態是LFSR的初始值,也稱為種子。反饋多項式是一個二進制多項式,用來確定反饋環路的連線方式。位數是LFSR的長度,決定了LFSR所能產生的最大周期。
接下來,我們詳細介紹LFSR輸出序列的計算方法。LFSR的輸出序列可以通過迭代運算得到,每次迭代產生一個新的輸出值。具體計算步驟如下:
- 初始化:將初始狀態加載到LFSR的各觸發器中。
- 產生輸出:根據LFSR的反饋多項式,通過異或門計算得到一個新的輸出位。
- 更新狀態:將LFSR的內部狀態向右位移一位,并將新的輸出位放入最低位。
重復以上步驟,直到滿足需求,可以得到LFSR的輸出序列。
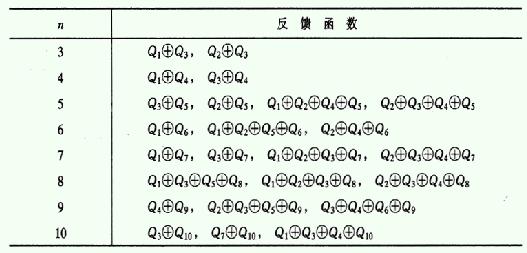
在計算LFSR輸出序列時,關鍵是確定反饋多項式。反饋多項式通常表示為一個二進制數,其中第一個和最后一個比特位之間的連線表示異或門的輸入。例如,反饋多項式1011表示將第1和第4觸發器的輸出異或,作為新的輸出位。
隨著迭代運算的進行,LFSR的狀態會不斷變化,從而產生一個長周期的輸出序列。當LFSR的內部狀態重復時,輸出序列也將首次出現重復。輸出序列的周期取決于LFSR的位數和反饋多項式。如果LFSR的位數為n,反饋多項式的次數為m,則LFSR的最大周期為2^n - 1,當且僅當反饋多項式是一個本原多項式時,LFSR才能產生最長周期的輸出序列。
線性反饋移位寄存器在密碼學和通信領域中有著廣泛的應用。在密碼學中,LFSR可以用于產生偽隨機數序列,用作加密算法的密鑰或填充。在通信中,LFSR可以用于編碼和解碼,用于糾錯碼或分組碼。此外,LFSR還可以用于信號調制、頻率合成和模擬電路測試。
在數值計算中,LFSR也有著重要的應用。LFSR可以被看作是一個時序差分方程,可以用于模擬線性時不變離散系統。此外,LFSR還可以用于生成正交序列、擴頻序列等,廣泛應用于無線通信和信號處理中。
綜上所述,線性反饋移位寄存器是一種重要的序列發生器,具有廣泛的應用。在本文中,我們詳細介紹了LFSR的工作原理、輸出序列的計算方法以及其在密碼學、通信和數值計算中的應用。
-
二進制
+關注
關注
2文章
795瀏覽量
41643 -
發生器
+關注
關注
4文章
1368瀏覽量
61677 -
移位寄存器
+關注
關注
3文章
258瀏覽量
22265 -
LFSR
+關注
關注
0文章
16瀏覽量
12744
發布評論請先 登錄
相關推薦
線性反饋移位寄存器原理與實現
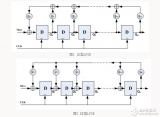
基于matlab的移位寄存器法m序列的產生
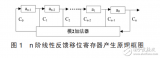
移位寄存器的特點_移位寄存器工作原理
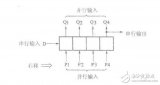
移位寄存器怎么用_如何使用移位寄存器_移位寄存器的用途
移位寄存器的原理
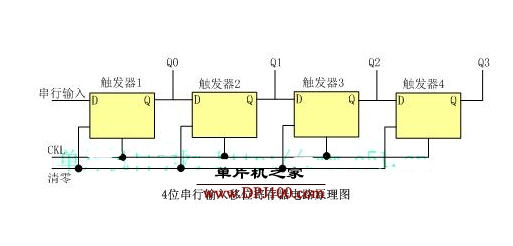




 線性反饋移位寄存器輸出序列怎么算
線性反饋移位寄存器輸出序列怎么算










評論