求解耦合電感并聯(lián)的等效電感的方法有多種,下面將解釋兩種方法:直接相加法和矩陣法。
- 直接相加法:
耦合電感并聯(lián)的等效電感值可以通過將每個獨(dú)立的電感相加得到。假設(shè)有兩個電感L1和L2并聯(lián),它們之間存在耦合系數(shù)k。則它們的等效電感可以表示為L12。
L12 = L1 + L2 + 2M
其中,M表示耦合電感,根據(jù)定義,有M = k √(L1 ? L2)。
因此,L12 = L1 + L2 + 2k √(L1 ? L2)。
這就是直接相加法。 - 矩陣法:
矩陣法是一種比較復(fù)雜的方法,但它可以方便地求得多個電感并聯(lián)的等效電感,特別是在有多個電感或者復(fù)雜電路中應(yīng)用較多。以下是具體步驟:
a) 構(gòu)造阻抗矩陣:
首先,將每個電感表示為一個阻抗元素。對于每個電感Li,可以通過Li = jωLi進(jìn)行表示,其中j是虛數(shù)單位,ω是角頻率。然后,將這些阻抗元素構(gòu)建成一個n×n的矩陣,其中n是并聯(lián)電感的個數(shù)。這個矩陣被稱為阻抗矩陣Z。
b) 耦合系數(shù)矩陣:
然后,構(gòu)造一個n×n的耦合系數(shù)矩陣K,其中Kij表示電感Li和Lj之間的耦合系數(shù)。如果電感Li和Lj之間沒有耦合,則Kij等于0。如果它們之間有耦合,則根據(jù)具體情況確定耦合系數(shù)的值。
c) 等效電感矩陣:
接下來,計(jì)算等效電感矩陣L。等效電感矩陣L可以通過下式計(jì)算得到:
L = (Z^-1 - K)?1
其中Z^-1是阻抗矩陣Z的逆矩陣。
d) 等效電感:
最后,等效電感是等效電感矩陣的主對角線上元素的和,即L12 = L11 + L22 + ... + Lnn。
通過上述步驟,可以求解耦合電感并聯(lián)的等效電感。這種方法可以應(yīng)用于多個電感的情況,并且具有較高的求解精度。
綜上所述,可以看出,求解耦合電感并聯(lián)的等效電感的方法有直接相加法和矩陣法。直接相加法較為簡單,適用于只有少量電感的情況。而矩陣法比較復(fù)雜,但適用于有多個電感或復(fù)雜電路的情況,具有較高的求解精度。
-
電路
+關(guān)注
關(guān)注
173文章
6022瀏覽量
174527 -
電感
+關(guān)注
關(guān)注
54文章
6193瀏覽量
103763 -
矩陣
+關(guān)注
關(guān)注
1文章
434瀏覽量
35062 -
耦合電感
+關(guān)注
關(guān)注
0文章
77瀏覽量
20372
發(fā)布評論請先 登錄
兩個沒有耦合關(guān)系的電感串聯(lián)或者并聯(lián)會發(fā)生什么
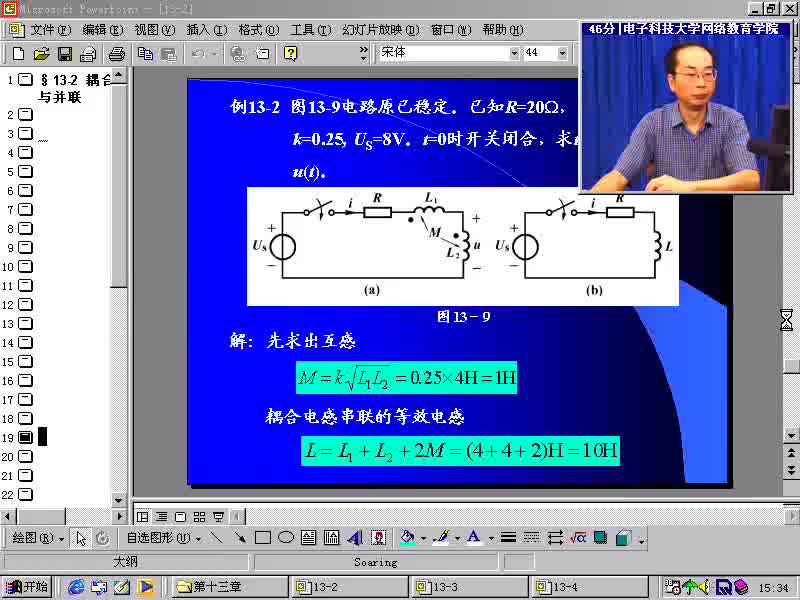
#硬聲創(chuàng)作季 #電路分析 電路分析基礎(chǔ)-61 耦合電感的串并聯(lián)及去耦等效電路-1
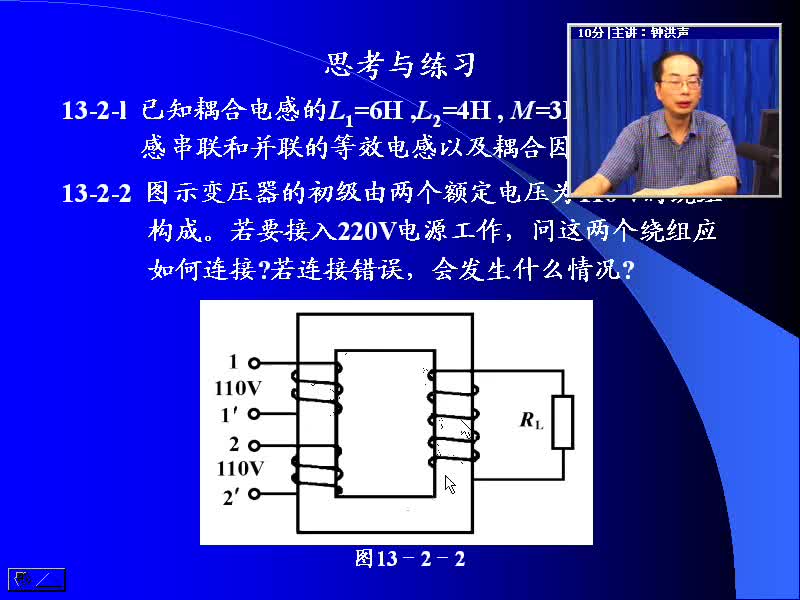
#硬聲創(chuàng)作季 #電路分析 電路分析基礎(chǔ)-61 耦合電感的串并聯(lián)及去耦等效電路-2

#硬聲創(chuàng)作季 #電路分析 電路分析基礎(chǔ)-61 耦合電感的串并聯(lián)及去耦等效電路-3
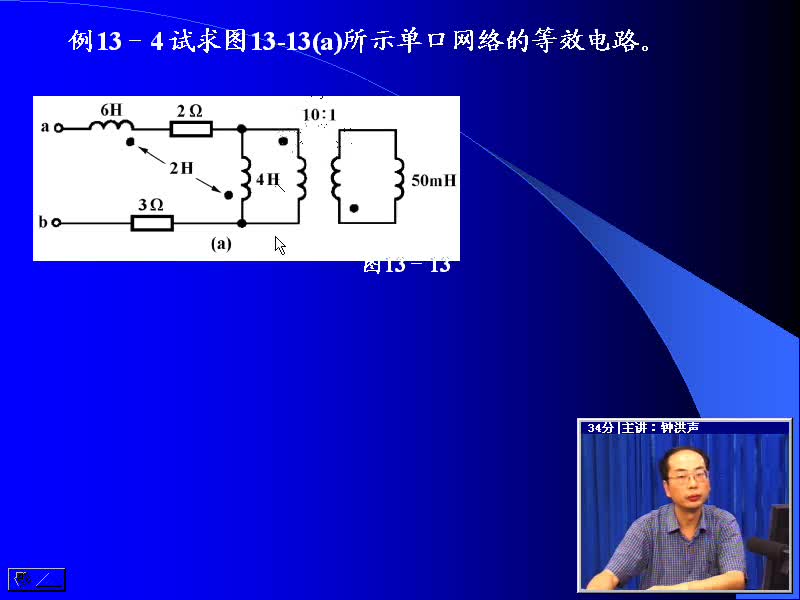
#硬聲創(chuàng)作季 #電路分析 電路分析基礎(chǔ)-61 耦合電感的串并聯(lián)及去耦等效電路-4
怎樣去計(jì)算有互感電感串并聯(lián)的等效電感
四相交錯并聯(lián)變換器中耦合電感的對稱化
耦合電感輔助換流的并聯(lián)諧振直流環(huán)節(jié)逆變器_王強(qiáng)
電感串聯(lián)和電感并聯(lián)時總電感量怎么算
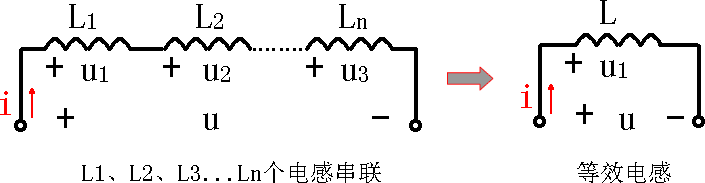
耦合電感的伏安特性是什么
電感串聯(lián)和電感并聯(lián)時總電感量怎么算?


















評論