昨天,有位號友問我本振相噪計算的問題。
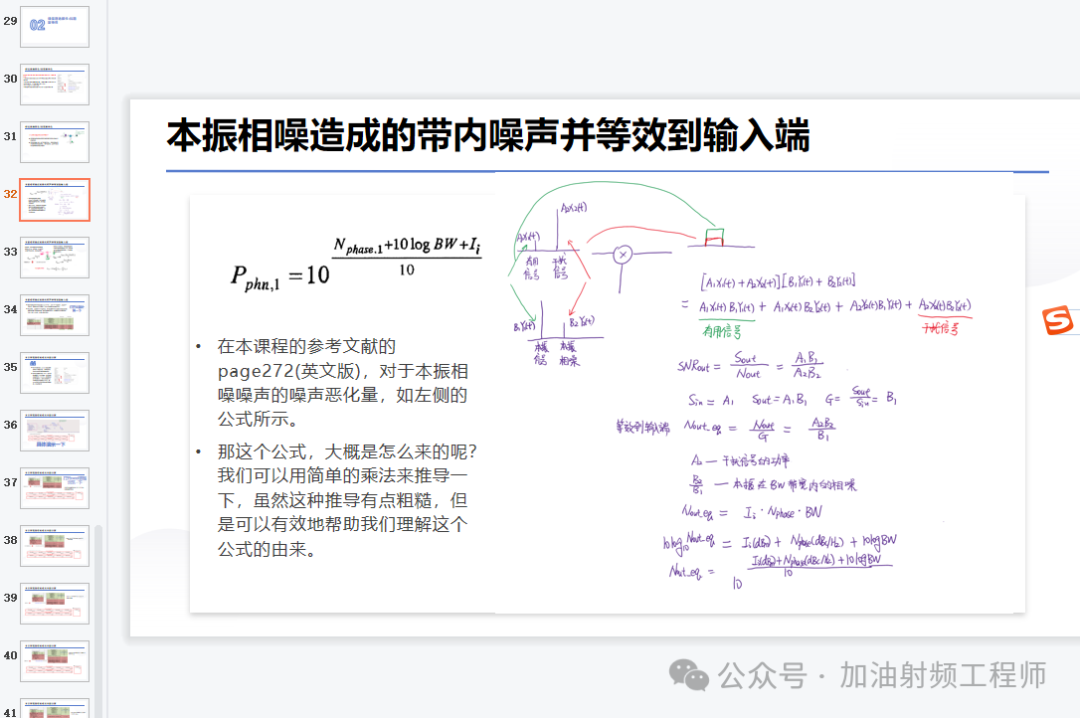
這個問題,在以前的公眾號文章上,有描述到過,具體如下圖所示。
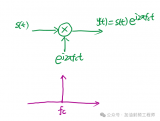
核心思想,就是把相噪和信號都看成單獨的信號,通過混頻器的時候,就是信號相乘。

這個思想,其實不止用于上述輸出相噪的計算。
只要涉及到了混頻器和本振,都差不多可以應用這種思想。
(3)
比如說,接收機的抗干擾性能,相關計算公式的由來,也是基于這個思想,就如在底部海報所示的課程中有講到的那樣。
在[1]中的page272頁中的抗干擾性能的公式,可以大概用這種思想推導出來。
(4)
然后,還有本振相噪與鏈路信號的EVM之間的關系。
那要了解這個,其實是分兩步走,第一步是本振相噪與輸出SNR之間的關系,第二步,就是輸出SNR與EVM之間的關系。
首先看,本振相噪與輸出SNR之間的關系。
本振相噪與輸出SNR之間的關系,其實就類比于在文章開頭,號友的問題。
不過,這邊的噪聲,需要在信道帶寬內做積分,不再是單獨的某一偏移頻率處的值。
先積分算出,在某一帶寬內的相噪的總和,進而算出本振的SNR,這樣就能算出輸出信號的SNR。
如果說,輸入信號的SNR遠優于本振相噪的SNR,假設為無限大,那么由(2)中的公式,就能推出輸出信號的SNR=本振信號的SNR。
接著看,輸出SNR與EVM之間的關系[2]。
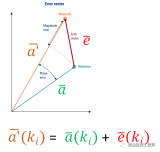
EVM是衡量星座圖中,理想點與實測點之間誤差的RMS值,假設,實測點為Sn,理想點為S0,n,相應的坐標如下圖所示。
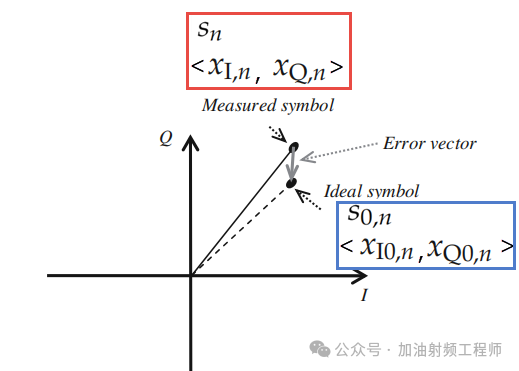
所以EVM可以用下式進行表示:

nI,n和nQ,n分別表示噪聲的I分量和Q分量,為理想點向量與測量點向量的差值。
所以從上式可以看出:

兩步連起來,就可以得到,本振相噪對輸出信號EVM的影響。
(5)
所以,看起來是三個不同的問題,三個不同的應用場景,光看最頂層的公式的話,三者之間并沒有什么聯系。
但是,如果往底層挖的話,發現這三者都是基于同一種思想,同一個公式,因為這三個都是與混頻器的數學模型相關。
審核編輯:劉清
-
混頻器
+關注
關注
10文章
681瀏覽量
45751 -
SNR
+關注
關注
3文章
195瀏覽量
24449 -
相噪
+關注
關注
0文章
5瀏覽量
2056
原文標題:本振相噪在射頻收發系統中的影響,我覺得都可以歸因到一個公式
文章出處:【微信號:加油射頻工程師,微信公眾號:加油射頻工程師】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
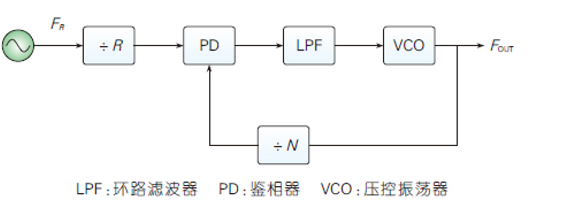
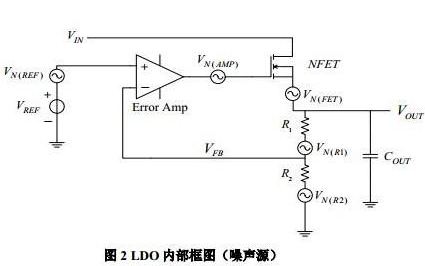
LDO環路穩定性及其對射頻頻綜相噪的影響
本振頻率100MHz發射到射頻端口測得很多奇次諧波
請問AD9361在射頻輸出端只能看到-55dB左右的本振信號正常嗎?
利用諧波混頻的微波低相噪鎖相設計介紹
LDO噪聲對射頻頻綜輸出相噪的影響介紹
本振泄露是什么_本振泄露的原因和影響
振芯科技儲備5G相關射頻收發技術
面向5G毫米波通信系統的本振源設計與實現分析



















評論