共讀好書
SPC—統計過程控制,要解決兩個問題:1.過程穩定不穩定?2.過程能力夠不夠?穩不穩定的問題,依靠“控制圖”來解決;能力夠不夠的問題,依靠“過程能力”來解決。
01 控制圖,是質量管理先驅休﹒哈特(見圖一)帶領團隊開發出來的

圖一休·哈特
它是將正態分布圖逆時針旋轉90°得到的,取±3σ(標準差)作為控制限。控制圖由三部分組成:1)數據點;2)中心線centerline=CL;3)控制限UCL/LCL=X± 3σ,如圖二所示。
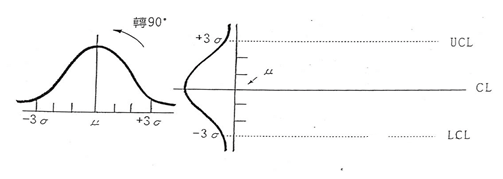
圖二控制圖的組成
控制圖的理論依據有兩個:1.質量波動原理;2.小概率事件。因此控制圖有一定的抽樣風險(錯報或漏報),降低風險可借助8條判異原則,如圖三所示。這8條判異原則可借助1、(2、3) 、(4、5) 、 6、8 、9、14 、15這些數字來方便記憶。
| 典型特殊原因識別準則的匯總 | |
| 1 | 一個點遠離中心線超過3個標準差 |
| 2 | 連續9點位于中心線一側 |
| 3 | 連續6點上升或下降 |
| 4 | 連續14點交替上下變化 |
| 5 | 2/3的點距中心線的距離超過2個標準差(同一側) |
| 6 | 4/5的點距中心線的距離超過1個標準差(同一側) |
| 7 | 連續15個點排列在中心線1個標準差范圍內(任一側) |
| 8 | 連續8個點距中心線的距離大于1個標準差(任一側) |
圖三 8條判異原則
控制圖跟數據類型有關,不同的數據類型對應不同的控制圖,其對應關系如圖四所示。
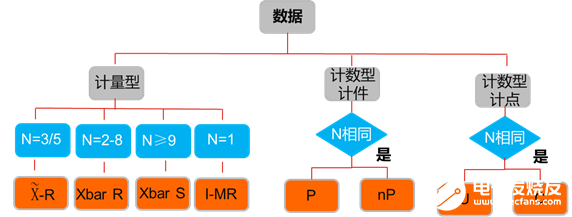
圖四數據類型與控制圖對應關系
控制圖中最常用是均值—極差圖,即Xbar—R控制圖,其中心線和控制限的計算公式如下:

圖五Xbar—R圖中心線和控制限的計算公式
02 過程能力以最常用的過程能力指數—Cpk來說明
過程能力指數—Cpk,是指過程的加工質量滿足技術標準的能力,計算公式Cpk=min{(USL-Xbar)/3σ,(Xbar-LSL)/3σ}。他的應用條件是過程穩定且數據是正態分布的質量特性。
過程能力指數Cpk值的評價參考標準如下:
| Cpk值的范圍 | 過程能力的評價參考 |
| Cpk≥1.67 | 過程能力滿足要求,可簡化質量檢驗工作 |
| 1.33≤ Cpk < 1.67 | 過程能力尚可,但需要改善 |
| 1.00≤ Cpk< 1.33 | 過程能力不足 |
在中心值無偏移的情況下,Cpk值與不良PPM對應關系如下:
| Cpk值 | 不良PPM |
| 1.0 | 2700 |
| 1.33 | 63 |
| 1.67 | 0.57 |
03 掌握了控制圖和過程能力指數Cpk的知識后,你就可以輕松地按照如下步驟導入SPC
步驟1:確定質量指標,收集數據。一般取25個子組,子組大小為5。如對5A管梁左段孔徑5.5±0.1mm尺寸進行連續抽樣,并記錄在預先設計好的表格中,數據如下:
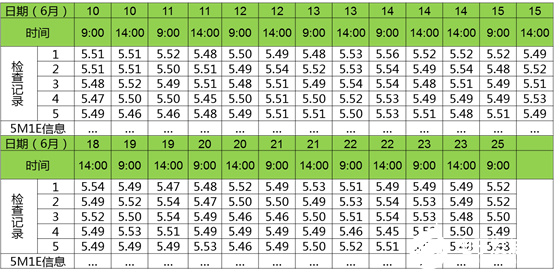
步驟2:計算觀測值的總均值X=5.50,平均極差R=0.05。
步驟3:計算R圖控制線、X圖控制線,并作圖。
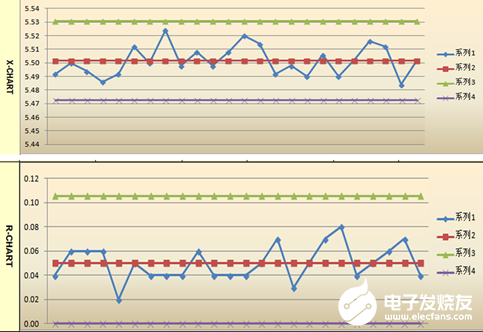
步驟4:依據判異原則判定,其生產過程處于穩定受控狀態。
步驟5:計算過程能力指數Cpk=1.57,能力尚可,滿足技術要求。
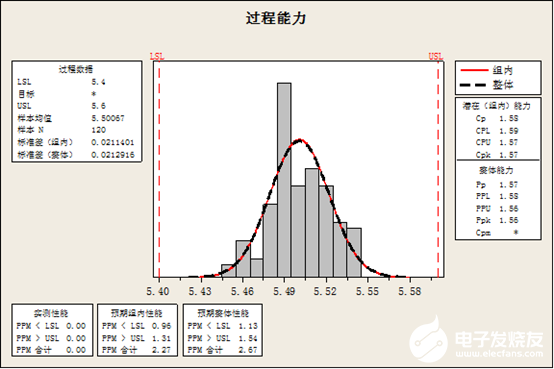
步驟6:延長X-R控制圖的控制線,作控制用控制圖,進行日常管理。
審核編輯 黃宇
-
SPC
+關注
關注
1文章
55瀏覽量
12147
發布評論請先 登錄
相關推薦

什么是光子學?
SPC軟件:MAISSE-SOFT原廠服務,全程護航,品質保障新高度!
SPC統計過程控制系統解決方案

SPC軟件在質量管理中的應用
Minitab實時SPC改變質量管理的5種方式
使用en.SPC5Studio-6.0.0-Green來編程,怎么將程序下載到MCU主控中呢?
SENT協議SPC功能是做什么用的?
使用TC27xD實現SPC通信,如何設置AURIX pincfg?
掌握電力質量的關鍵工具:恒峰HFQ-SPC1000電能質量分析儀

華為交換機最簡單的入門配置,一學就會




 一學就會的SPC
一學就會的SPC












評論