機器學(xué)習與線性回歸

或許我們所有人都會學(xué)習的第一個機器學(xué)習算法就是線性回歸算法，它無疑是最基本且被廣泛使用的技術(shù)之一——尤其是在預(yù)測分析方面。

線性回歸的主要優(yōu)勢在于其簡單性，可以相當容易地實施。而簡單意味著該算法也具有很高的可解釋性。

本質(zhì)上，線性回歸試圖通過將線性方程擬合到觀測數(shù)據(jù)點來對給定數(shù)據(jù)集進行建模。

因此，這里的關(guān)鍵概念是線性。假設(shè)我們的特征（可以是一個或多個）與某個目標對象之間存在線性關(guān)系。

這種線性可以通過以下形式的方程表示：

y = β0 + β1x1 + β2x2 + ... + βn*xn + ε

其中：

y 是因變量（我們試圖預(yù)測的結(jié)果）。

x1, x2, ..., xn 是自變量（預(yù)測因子）。

β0, β1, ..., βn 是系數(shù)，代表每個預(yù)測因子與因變量之間的量化關(guān)系。

ε 是誤差項，用于解釋 y 中未被 x 變量解釋的變異性。

線性回歸模型的目標是以這樣一種方式估計這些系數(shù)，即最小化殘差（觀測值 (y) 與模型預(yù)測值之間的差異）。

線性回歸在建模計數(shù)的局限性

計數(shù)數(shù)據(jù)的本質(zhì)

計數(shù)數(shù)據(jù)指的是代表事件發(fā)生次數(shù)或發(fā)生數(shù)量的數(shù)據(jù)——呼叫中心接收的電話數(shù)量或商店的銷售交易數(shù)量。

這類數(shù)據(jù)本質(zhì)上是離散的且非負的。

線性回歸在處理計數(shù)數(shù)據(jù)時的不足

盡管線性回歸應(yīng)用廣泛，但在應(yīng)用于計數(shù)數(shù)據(jù)時面臨某些局限性：

負數(shù)預(yù)測問題

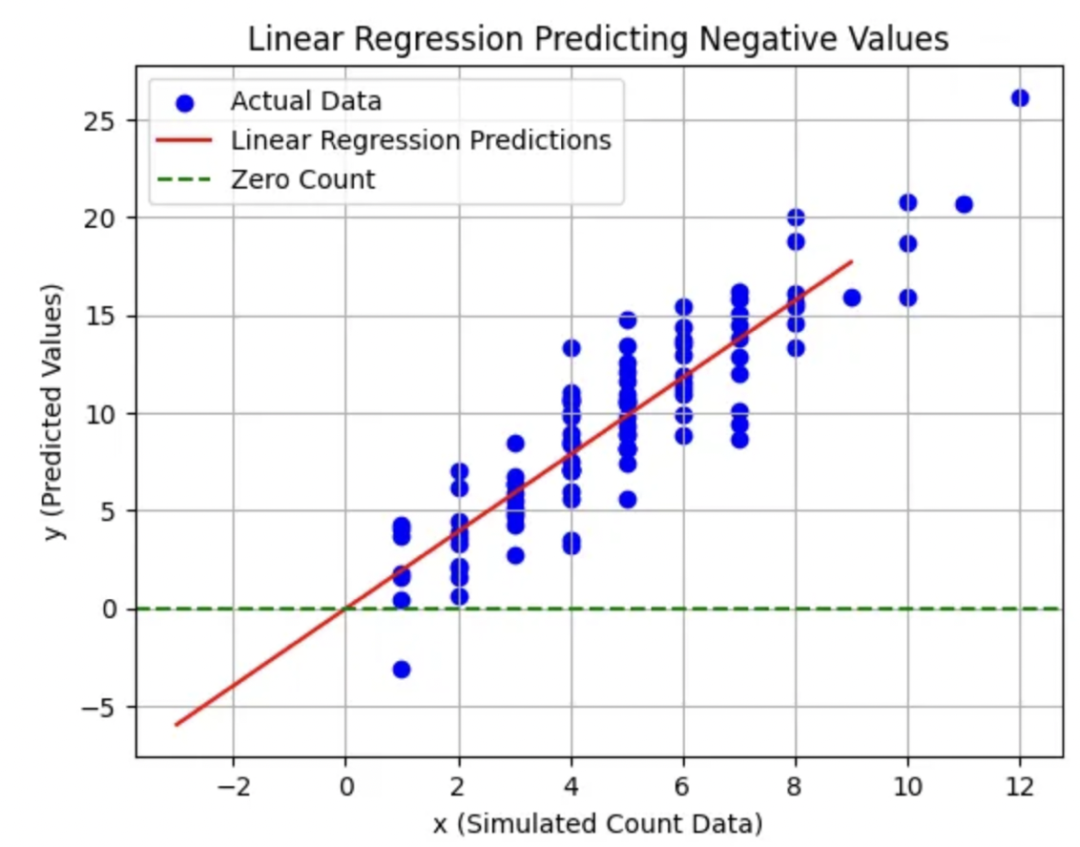
線性回歸有時可能會為計數(shù)數(shù)據(jù)預(yù)測出負數(shù)值，這在現(xiàn)實世界場景中是不合理的。

這是將線性回歸應(yīng)用于非負計數(shù)數(shù)據(jù)時的一個根本性缺陷。

例如，預(yù)測“-2個電話接聽”是不合理的。

考慮下面的例子：

importnumpyasnp
importmatplotlib.pyplotasplt
fromsklearn.linear_modelimportLinearRegression

#Simulatingcountdata
np.random.seed(0)
x=np.random.poisson(5,100)#SimulatingcountdatawithaPoissondistribution
y=2*x+np.random.normal(0,2,100)#Addingsomenoise

#LinearRegressionModel
model=LinearRegression()
model.fit(x.reshape(-1,1),y)

#Predictionsincludingnegativevalues
x_test=np.array(range(-3,10))#Includingnegativevaluestoillustratetheissue
y_pred=model.predict(x_test.reshape(-1,1))

#Plotting
plt.scatter(x,y,color='blue',label='ActualData')
plt.plot(x_test,y_pred,color='red',label='LinearRegressionPredictions')
plt.axhline(0,color='green',linestyle='--',label='ZeroCount')
plt.xlabel('x(SimulatedCountData)')
plt.ylabel('y(PredictedValues)')
plt.title('LinearRegressionPredictingNegativeValues')
plt.legend()
plt.grid(True)
plt.show()

正態(tài)分布殘差的問題

線性回歸的另一個局限性是其假設(shè)殘差（觀測值與預(yù)測值之間的差異）呈正態(tài)分布。這個假設(shè)在計數(shù)數(shù)據(jù)上往往不成立，尤其是當平均計數(shù)較低時，會導(dǎo)致分布偏斜。計數(shù)數(shù)據(jù)的分布通常是偏斜的，不像正態(tài)分布那樣對稱。

讓我們在Python中演示這一點。

#Calculatingresiduals
y_pred_actual=model.predict(x.reshape(-1,1))
residuals=y-y_pred_actual

#Plottingresiduals
plt.hist(residuals,bins=20,color='grey',edgecolor='black')
plt.axvline(0,color='red',linestyle='--')
plt.xlabel('Residuals')
plt.ylabel('Frequency')
plt.title('DistributionofResidualsinLinearRegression')
plt.grid(True)
plt.show()

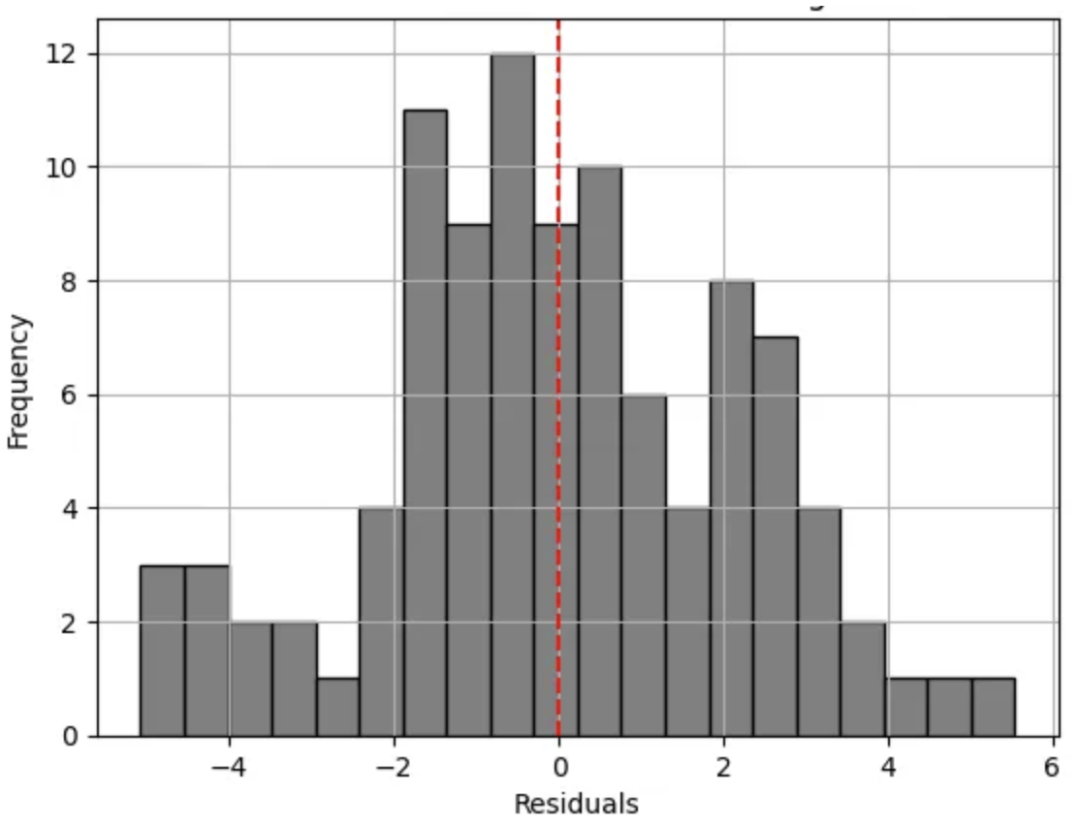
觀察上述直方圖，我們可以立即觀察到它的多峰（即存在多個峰值）特征。因此，這一特征使我們偏離了預(yù)期的鐘形分布（對于正態(tài)分布的殘差）。由此，我們可以清楚地看到這已經(jīng)違反了線性回歸的假設(shè)。

另一個需要注意的關(guān)鍵點是殘差的擴散。觀察直方圖時，我們可以看到它相當寬——表明方差變化較大。對于一個擬合良好的模型，殘差的擴散應(yīng)該盡可能窄（即預(yù)測值接近實際值）。

以上幾點表明，簡單線性模型并未充分捕捉到關(guān)系。此外，輕微的偏斜和潛在的異常值指出了模型在為所有觀測值做出準確預(yù)測方面的局限性。

深入探討泊松回歸

當我們處理計數(shù)數(shù)據(jù)時，泊松回歸確實能提供很大幫助。計數(shù)數(shù)據(jù)本質(zhì)上包含非負整數(shù)，而在對此類數(shù)據(jù)進行建模時，與線性回歸相比，泊松回歸提供了一個更合適的框架。

理解泊松回歸

泊松分布是一種離散概率分布，它表達了在已知的恒定平均率下，固定時間或空間間隔內(nèi)發(fā)生特定數(shù)量事件的概率，并且這些事件的發(fā)生是相互獨立的，不受上一次事件發(fā)生以來時間的影響。

泊松分布的關(guān)鍵特性：

均值和方差相等——隨著平均發(fā)生次數(shù)的增加，計數(shù)的變異性也隨之增加。

它為固定時間或空間間隔內(nèi)事件發(fā)生的次數(shù)分配概率，但前提是這些事件發(fā)生在恒定速率下且彼此獨立。

**泊松回歸應(yīng)用場景

在泊松回歸中，我們將預(yù)期計數(shù)的對數(shù)作為自變量的線性函數(shù)來建模。

我們可以表示如下：

log(λ) = β0 + β1x1 + β2 * x2 + ... + βnxn

其中 λ 代表預(yù)期計數(shù)或發(fā)生率。

泊松回歸模型的解釋

泊松回歸模型中的系數(shù)解釋了在保持所有其他預(yù)測變量不變的情況下，預(yù)測變量每單位變化所導(dǎo)致的預(yù)期計數(shù)的對數(shù)變化。

泊松回歸與線性回歸之間的主要差異

殘差的分布：泊松回歸不假設(shè)殘差呈正態(tài)分布；相反，它假設(shè)數(shù)據(jù)遵循泊松分布，這對于計數(shù)數(shù)據(jù)通常更為合適。

處理非負計數(shù)：泊松回歸固有地處理非負整數(shù)計數(shù)，確保模型不會預(yù)測負數(shù)。

讓我們用Python來演示如何應(yīng)用泊松回歸。

importnumpyasnp
importmatplotlib.pyplotasplt
importstatsmodels.apiassm

#Simulatingcountdata
np.random.seed(0)
x=np.random.normal(5,2,100)#Independentvariabledata
y=np.random.poisson(np.exp(x*0.1))#Simulatedcountdata

#PoissonRegressionModel
exog,endog=sm.add_constant(x),y
poisson_model=sm.GLM(endog,exog,family=sm.families.Poisson()).fit()

#Predictionsandplot
x_test=np.linspace(min(x),max(x),100)
y_pred=poisson_model.predict(sm.add_constant(x_test))

plt.scatter(x,y,color='blue',label='ActualCountData')
plt.plot(x_test,y_pred,color='red',label='PoissonRegressionPredictions')
plt.xlabel('IndependentVariable(x)')
plt.ylabel('ExpectedCount(y)')
plt.title('PoissonRegressiononCountData')
plt.legend()
plt.grid(True)
plt.show()

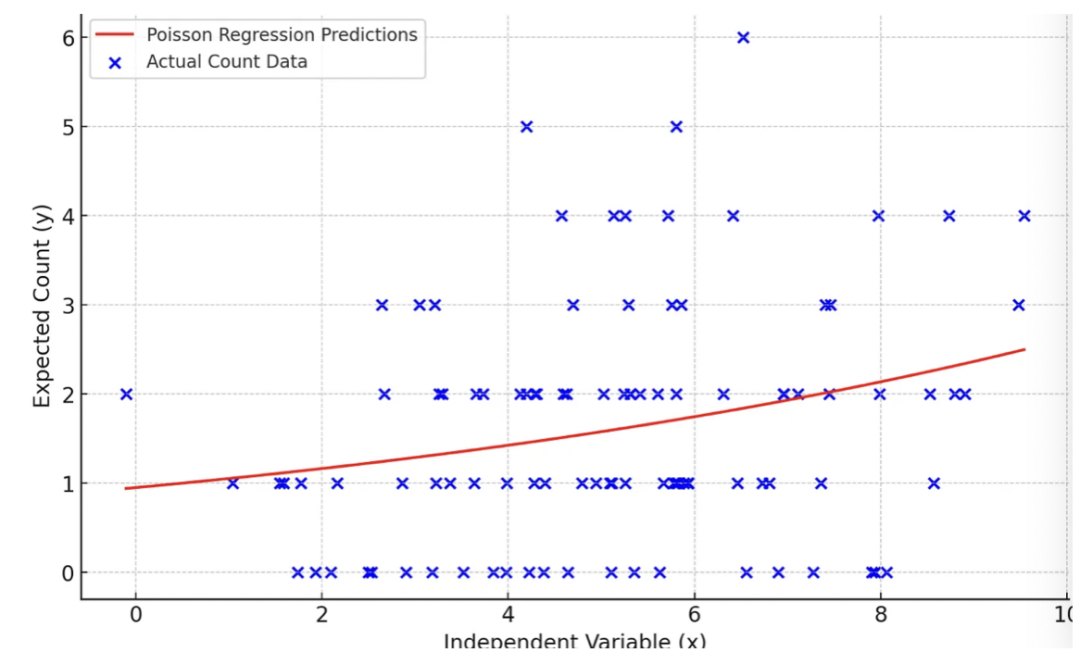
一些關(guān)鍵觀察結(jié)果：

預(yù)測線（紅色）不是直線。這表明了自變量和預(yù)期計數(shù)之間的對數(shù)關(guān)系，這是泊松回歸的一個關(guān)鍵特征。

該模型預(yù)測，隨著 x 的增加，預(yù)期計數(shù)（y）也增加，但不是以恒定速率增加（由于對數(shù)鏈接函數(shù)）。

與線性回歸不同，泊松回歸模型不預(yù)測負數(shù)計數(shù)。所有預(yù)測值都是非負的，這對于計數(shù)數(shù)據(jù)是合適的。

預(yù)測線似乎捕捉到了實際數(shù)據(jù)的一般趨勢，表明這個模擬數(shù)據(jù)集有一個合理的擬合。這清楚地展示了泊松回歸在建模計數(shù)數(shù)據(jù)時的適用性。

這清楚地展示了泊松回歸在建模計數(shù)數(shù)據(jù)時的適用性。

該模型考慮了計數(shù)的非負性和它們的分布性質(zhì)。

與線性回歸不同，泊松回歸可以處理計數(shù)數(shù)據(jù)的方差結(jié)構(gòu)，其中方差與均值成正比，使其成為計數(shù)數(shù)據(jù)分析的有力工具。

結(jié)論

關(guān)鍵點回顧

在本文中，我們探討了線性回歸的基本方面以及其在應(yīng)用于計數(shù)數(shù)據(jù)時的局限性。

我們發(fā)現(xiàn)線性回歸可能預(yù)測出負值，并對殘差的分布做出假設(shè)，這些假設(shè)對于本質(zhì)上是非負的且通常是偏斜的計數(shù)數(shù)據(jù)并不成立。然后，我們引入了泊松回歸作為計數(shù)數(shù)據(jù)的健壯替代方案。泊松回歸旨在處理非負整數(shù)，并適應(yīng)數(shù)據(jù)中特有的計數(shù)方差。

模型選擇的重要性

統(tǒng)計模型的選擇至關(guān)重要，可以顯著影響從數(shù)據(jù)中得到的洞察。

理解數(shù)據(jù)的本質(zhì)和不同模型背后的假設(shè)至關(guān)重要。

通過選擇最適合數(shù)據(jù)特征的模型，我們確保更準確、可靠和有意義的預(yù)測。

審核編輯：劉清