1. 項目概述
項目說明
該項目的目標是創建一個用DE1-SOC進行硬件加速的2D N-Body重力模擬器。

該模擬器擁有可定制的地圖和基于鼠標的 GUI 交互功能。
使用標準CPU模擬天體(恒星、行星、小行星等)之間的引力是有限的,因為它只能進行順序計算,隨著天體數量的增加,模擬時間會很長。而該項目是通過將每個天體的信息發送到FPGA來加速這些計算,讓它并行計算其他天體之間的每次交互,然后將結果發送回ARM繼而顯示在顯示器上。
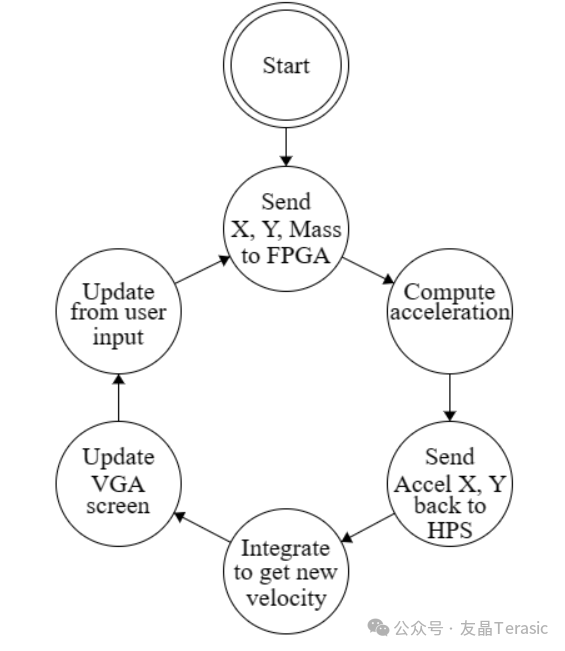
2. 數學原理
加速器的數學基礎從標準牛頓重力方程開始:
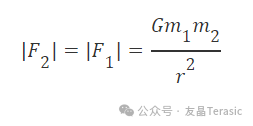
為了簡化方程并減少 HPS 處理的計算量,先這樣求解加速度:


然后用同樣的方法計算其他加速度:
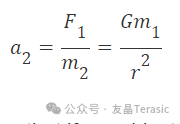
不過,對于這個計算,
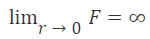
這意味著如果物體靠得太近,會產生無限的加速度。這與現實不符,且由于該系統不處理對象的碰撞,因此需要添加不出故障的計算進去。
如果用一個偏移量epsilon來規范半徑數學計算,就可阻止加速度增加到無窮大。

當選擇epsilon取值是10的負8次方時,這意味著它不會明顯超出尾數的精度也就是小數點后9位。


但是這只計算了總加速度。為了將加速度存儲為矢量,則這里需要方向分量。為了計算這個,就用x和y的位移除以半徑。
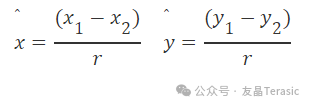
當應用到之前的加速度公式時得到了下面的方程:
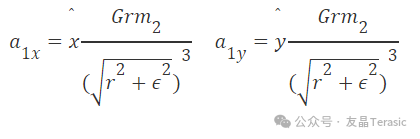
給物體2的加速度加上一個負號因為位移是我們在原始x^計算中計算的負的位移。
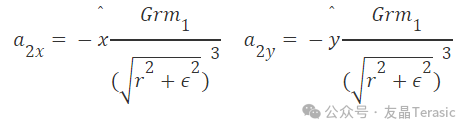
由于無法快速執行浮點除法,因此在計算中只能進行3種不同的操作。加/減,乘和反平方根(使用快速反平方根算法)。下面的操作用于計算加速器中的最終結果。首先用2個加法器計算半徑的平方來計算x和y的位移,然后將輸出與其自身相乘并求出它們的和,也就是半徑的平方。
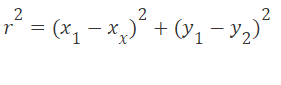
一旦有了半徑的平方,就可以試著用半徑平方的平方根的倒數來計算半徑的倒數。
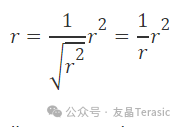
用半徑平方和epsilon平方之和的平方根的倒數,可以用下面的方法計算出前面所述的加速度方程:
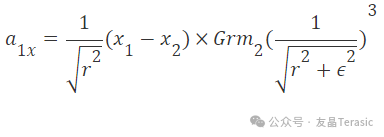
更多原理介紹和方法實現請參考項目原文。
審核編輯:劉清
-
FPGA
+關注
關注
1629文章
21729瀏覽量
602986 -
ARM
+關注
關注
134文章
9084瀏覽量
367381 -
模擬器
+關注
關注
2文章
874瀏覽量
43208 -
GUI
+關注
關注
3文章
659瀏覽量
39654 -
硬件加速器
+關注
關注
0文章
42瀏覽量
12763
原文標題:FPGA開源項目分享——2D N-Body重力模擬器
文章出處:【微信號:友晶FPGA,微信公眾號:友晶FPGA】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
DE1-SOC新貨轉讓
DE1-SoC官方自帶ControlPanel代碼解讀與AV圖像采集處理?
小弟求購Altera DE1-SOC開發板,哪位大神玩剩下了傳承一下,多謝!
de1-soc FPGA(Quartus工程含Qsys系統) + HPS 操作步驟
基于VxWorks的硬件加速技術探討

如何在DE1-SOC開發板上搭建NIOS II處理器運行UCOS
基于VxWorks的硬件加速技術探討
Veloce仿真環境下的SoC端到端硬件加速器功能驗證

DE1-SoC開發工具包的詳細用戶和使用手冊資料免費下載

ALTERA公司的DE1 SoC FPGA開發板的培訓教程免費下載
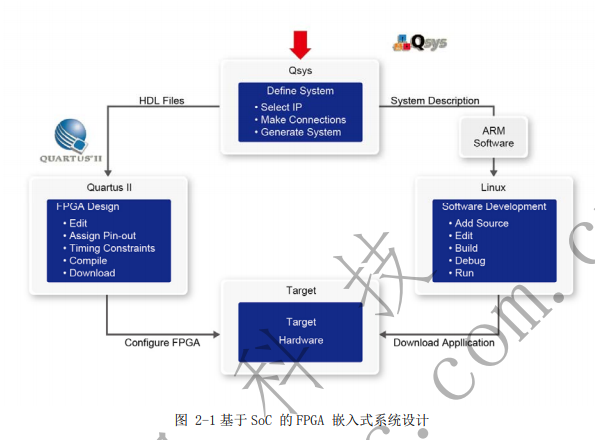




 用DE1-SOC進行硬件加速的2D N-Body重力模擬器設計
用DE1-SOC進行硬件加速的2D N-Body重力模擬器設計











評論