NVIDIA cuOpt 是一個(gè)用于解決復(fù)雜路徑問(wèn)題的加速優(yōu)化引擎。它能高效解決不同方面的問(wèn)題，如休息時(shí)間、等待時(shí)間、多個(gè)車(chē)輛成本和時(shí)間矩陣、多個(gè)目標(biāo)、訂單-車(chē)輛匹配、車(chē)輛起始和結(jié)束位置、車(chē)輛起始和結(jié)束時(shí)間等。

更具體地說(shuō)，cuOpt 所解決的諸多問(wèn)題可以歸為兩大類(lèi)：帶時(shí)間窗的擁擠車(chē)輛路徑問(wèn)題（CVRPTW）和帶時(shí)間窗的取送貨問(wèn)題（PDPTW）。這些問(wèn)題的目標(biāo)是在滿(mǎn)足客戶(hù)要求的同時(shí)，最大程度地減少車(chē)輛數(shù)量和總行程。

經(jīng) SINTEF 驗(yàn)證，過(guò)去三年中，cuOpt 在最大規(guī)模的路徑基準(zhǔn)測(cè)試中打破了 23 項(xiàng)世界紀(jì)錄。

本文將探討優(yōu)化算法的關(guān)鍵要素和定義，以及在基準(zhǔn)測(cè)試中比較 NVIDIA cuOpt 與該領(lǐng)域領(lǐng)先解決方案的過(guò)程，著重說(shuō)明進(jìn)行這些比較的重要意義。在本文中，我們使用“請(qǐng)求”一詞表示 CVRPTW 訂單以及 PDPTW 問(wèn)題中的取貨-交貨訂單對(duì)。

盡管該領(lǐng)域存在各種約束和問(wèn)題維度，但本文的討論范圍僅限于容量和時(shí)間窗約束。容量約束要求車(chē)輛上的商品總量在任何時(shí)候都不能超過(guò)車(chē)輛容量。時(shí)間窗約束則要求服務(wù)訂單的時(shí)間不能早于時(shí)間窗的開(kāi)始時(shí)間，也不能晚于時(shí)間窗的結(jié)束時(shí)間。

組合優(yōu)化

組合優(yōu)化問(wèn)題是世界上計(jì)算成本最高的問(wèn)題之一（NP-hard），搜索空間中可能狀態(tài)的數(shù)量是階乘的。由于不可能使用精確算法來(lái)解決大型問(wèn)題，因此需要使用啟發(fā)式算法來(lái)接近最優(yōu)解決方案。啟發(fā)式算法使用各種算法探索搜索空間，這些算法具有二次方或更高次方的計(jì)算復(fù)雜度。

高度的復(fù)雜性和問(wèn)題的性質(zhì)使得使用大規(guī)模并行 GPU 加速這些算法成為可能。借助 GPU 加速，可以在合理的時(shí)間內(nèi)獲得接近最優(yōu)的解決方案。

構(gòu)建進(jìn)化路徑優(yōu)化算法

典型的路徑求解器包括兩個(gè)階段：生成初始解決方案和改進(jìn)解決方案。本章將介紹生成初始解決方案和改進(jìn)解決方案的步驟。

初始解決方案生成算法

利用有限的車(chē)隊(duì)生成一個(gè)可行的初始解決方案并滿(mǎn)足所有約束條件，本身就是一個(gè) NP-hard 問(wèn)題。我們的團(tuán)隊(duì)對(duì)引導(dǎo)彈射搜索（GES）算法進(jìn)行了改進(jìn)和并行化，以便將請(qǐng)求放置到路徑上。

GES 的主要想法很簡(jiǎn)單。我們首先嘗試將請(qǐng)求插入路徑。如果插入該請(qǐng)求不可行，我們就從路徑中彈出一個(gè)或多個(gè)易于插入的請(qǐng)求，然后將該請(qǐng)求插入到放寬的路徑中。每個(gè)請(qǐng)求的懲罰分?jǐn)?shù)（p-score）表示將該請(qǐng)求插入路徑的難度。只有當(dāng)被彈出請(qǐng)求的 p 分?jǐn)?shù)之和小于所考慮的請(qǐng)求時(shí)，算法才會(huì)插入該請(qǐng)求。

無(wú)法將某個(gè)請(qǐng)求插入路徑時(shí)，我們就會(huì)遞增該請(qǐng)求的 p-score，然后再試一次。我們會(huì)將所有未提供服務(wù)的請(qǐng)求保留在彈出池中，算法會(huì)一直運(yùn)行到彈出池清空為止。換句話說(shuō)，它會(huì)一直運(yùn)行到所有請(qǐng)求都被服務(wù)為止。

這種算法的主要缺點(diǎn)是循環(huán)（返回到解決方案中的前一組節(jié)點(diǎn)）。當(dāng)彈射節(jié)點(diǎn)數(shù)量較多時(shí)，找到彈射組合的速度較慢。另一個(gè)缺點(diǎn)是只考慮弱的、隨機(jī)擾動(dòng)的解決方案。我們已經(jīng)消除了這些缺陷，能夠生成路徑數(shù)量遠(yuǎn)低于當(dāng)前最先進(jìn)方法的解決方案。

在深入探討彈射算法之前，了解可行性檢查和解決方案評(píng)估是在恒定時(shí)間內(nèi)通過(guò)時(shí)間扭曲法進(jìn)行的，這點(diǎn)十分重要。雖然這種方法大大縮短了計(jì)算時(shí)間，但由于需要遵守任意數(shù)量彈射搜索的詞典順序，因此也增加了并行化的難度。

查找哪些請(qǐng)求需要彈出，以及在何處可行地插入所考慮的請(qǐng)求是一個(gè)計(jì)算成本很高的問(wèn)題：它與彈出請(qǐng)求的數(shù)量成指數(shù)關(guān)系，并且需要檢查所有路徑中的所有插入位置。我們的實(shí)驗(yàn)表明，少量的彈出請(qǐng)求就會(huì)引發(fā)算法循環(huán)。

因此，我們提出了一種可以并行彈出多達(dá) 10 個(gè)請(qǐng)求（啟發(fā)式）和 5 個(gè)請(qǐng)求（當(dāng)進(jìn)行廣泛搜索時(shí)）的方法。我們將彈出算法并行化，從每個(gè)路徑中彈出一個(gè)片段，并在一個(gè)線程塊中處理這些臨時(shí)路徑。然后，嘗試在所有可能的位置并行插入所考慮的請(qǐng)求。

深度搜索算法會(huì)嘗試彈出路徑中所有請(qǐng)求的所有可能排列。我們將不同的線程塊用于每個(gè)請(qǐng)求插入位置，并通過(guò)將詞序拆分為獨(dú)立的子排列來(lái)并行執(zhí)行詞序搜索。

GES 算法循環(huán)運(yùn)行，直到耗盡時(shí)間或請(qǐng)求池為空。在每次迭代中，我們都會(huì)對(duì)解決方案進(jìn)行擾動(dòng)以改進(jìn)解決方案的狀態(tài)，并打開(kāi)解決方案中的缺口，從而找到可行的插入方案。擾動(dòng)是一種在路徑之間和路徑內(nèi)部隨機(jī)遷移和交換節(jié)點(diǎn)的隨機(jī)局部搜索。

在找到滿(mǎn)足要求的最佳車(chē)輛數(shù)量后，我們轉(zhuǎn)入改進(jìn)階段，該階段負(fù)責(zé)使目標(biāo)最小化。默認(rèn)情況下的目標(biāo)是總行駛距離，但也可以在 cuOpt 中配置其他目標(biāo)。

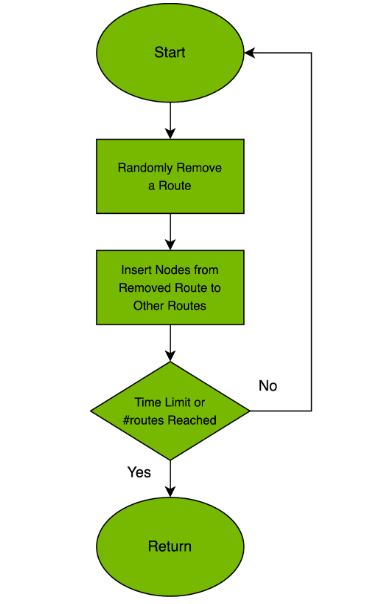
圖 1. NVIDIA cuOpt 中的 GES 算法流程圖

進(jìn)化過(guò)程和局部搜索算法

改進(jìn)階段使用進(jìn)化策略對(duì)多個(gè)解決方案進(jìn)行改進(jìn)，生成的解決方案被置于一個(gè)群體中。為了獲得足夠多樣化的初始解決方案，我們?cè)谏蛇^(guò)程中使用了隨機(jī)化技術(shù)。利用 GPU 架構(gòu)，我們可以并行生成許多不同的解決方案。多樣化群體會(huì)經(jīng)歷一個(gè)進(jìn)化改進(jìn)過(guò)程，而解決方案的最佳特性會(huì)保留在更新的幾代中。

在進(jìn)化過(guò)程的一個(gè)步驟中，我們采用兩個(gè)隨機(jī)解決方案并應(yīng)用交叉算子，這樣就會(huì)產(chǎn)生一個(gè)子代解決方案，它繼承了兩個(gè)親代的優(yōu)良特性。可以對(duì)解決方案應(yīng)用不同的交叉算子，其中一些算子會(huì)使子代處于不完整狀態(tài)。我們可以通過(guò)刪除重復(fù)節(jié)點(diǎn)、插入未選擇路徑的節(jié)點(diǎn)或?qū)ζ溥M(jìn)行不可行性局部搜索來(lái)修復(fù)解決方案。

例如，基于順序的交叉算子會(huì)根據(jù)節(jié)點(diǎn)在另一個(gè)父代解決方案中出現(xiàn)的順序，重新排列一個(gè)父代解決方案的一條或多條路徑中的節(jié)點(diǎn)。由此產(chǎn)生的子代保留了一個(gè)父代解決方案的分組屬性和另一個(gè)方案的排序?qū)傩浴＿@個(gè)特殊算子的結(jié)果是一個(gè)完整的解決方案，但就時(shí)間和容量限制而言，該解決方案很可能是不可行的。cuOpt 包含多個(gè)交叉算子，它們?cè)诮鉀Q方案上隨機(jī)執(zhí)行。

在這種情況下，交叉后的局部搜索階段在減少或消除不可行性，或提高總目標(biāo)或行程距離方面起著至關(guān)重要的作用。局部搜索的目標(biāo)權(quán)重取決于優(yōu)化的重要程度，較高的不可行性權(quán)重有助于將解決方案返回可行區(qū)域，這通常是大多數(shù)問(wèn)題的情況。

局部搜索為子代解決方案找到局部最小值，然后子代解決方案參與進(jìn)一步的進(jìn)化步驟。快速局部搜索至關(guān)重要，因?yàn)樗窃跁r(shí)間預(yù)算內(nèi)完成多少次改進(jìn)迭代的主要因素。我們使用快速、近似和大型鄰域搜索算法來(lái)找到性能良好的局部最小值。我們沒(méi)有像傳統(tǒng)方法那樣執(zhí)行固定大小的鄰域局部搜索，而是設(shè)計(jì)了一個(gè)“網(wǎng)”來(lái)快速捕捉容易改進(jìn)的地方，并在達(dá)到停滯時(shí)捕捉極深度算子。

快速算子能快速探索小鄰域，而近似算子每次應(yīng)用時(shí)都能評(píng)估不同的移動(dòng)，這一點(diǎn)尤為重要，因?yàn)榻徊娼?jīng)常會(huì)使某些路徑保持不變。正如在圖中尋找負(fù)子集相交循環(huán)的 GPU 并行算法中所解釋的，大型鄰域算子以路徑間的移動(dòng)循環(huán)表示的移動(dòng)鏈來(lái)移動(dòng)請(qǐng)求。

循環(huán)算子可以探索一個(gè)非常大的鄰域，而簡(jiǎn)單算子則無(wú)法探索該鄰域，這只是因?yàn)橄拗茥l件禁止這些簡(jiǎn)單算子通過(guò)搜索空間中的某些山。通過(guò)這種工作流，我們可以經(jīng)常使用快速算子，而較少使用計(jì)算成本較高的深度算子。

GPU 并行化是通過(guò)將每條假設(shè)路徑映射到一個(gè)線程塊來(lái)實(shí)現(xiàn)的。這樣就可以使用共享內(nèi)存來(lái)存儲(chǔ)與路徑相關(guān)的數(shù)據(jù)，這些數(shù)據(jù)在搜索移動(dòng)時(shí)是臨時(shí)的。臨時(shí)路徑要么是原始路徑的副本，要么是一個(gè)或多個(gè)請(qǐng)求被彈出的路徑。線程塊中的線程會(huì)嘗試將其他路徑中所有可能的請(qǐng)求插入臨時(shí)路徑的所有位置。

在找到并記錄所有移動(dòng)后，我們通過(guò)將每個(gè)路徑對(duì)的插入/彈出成本變量相加，找出每個(gè)路徑對(duì)的最佳移動(dòng)。成本變量使用目標(biāo)權(quán)重計(jì)算得出，其中還包含不可行性懲罰權(quán)重。如果多個(gè)移動(dòng)對(duì)所修改的路徑而言是互斥的，我們就會(huì)執(zhí)行多個(gè)這樣的移動(dòng)。

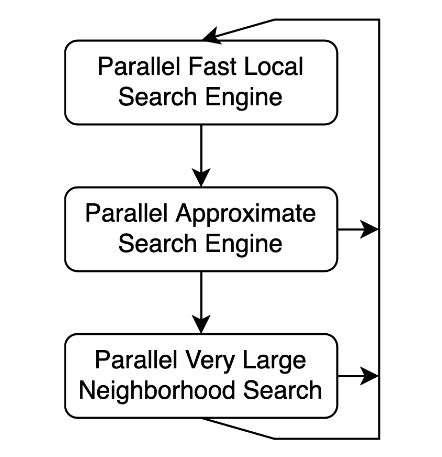
圖 2. NVIDIA cuOpt 中的局部搜索程序流程圖

對(duì) cuOpt 進(jìn)行基準(zhǔn)測(cè)試

我們不斷提高 cuOpt 的性能和質(zhì)量。為了衡量 cuOpt 的質(zhì)量，我們?cè)谘芯康米疃嗟幕鶞?zhǔn)測(cè)試（包括 Gehring & Homberger CVRPTW 基準(zhǔn)測(cè)試和 Li & Lim PDPTW 基準(zhǔn)測(cè)試）上將求解器與最著名的解決方案進(jìn)行了比較。在實(shí)踐中，求解器能多快得出所需的解決方案對(duì)企業(yè)非常重要。

評(píng)估標(biāo)準(zhǔn)和目標(biāo)

準(zhǔn)確度被定義為找到的解決方案與已知最佳解決方案（BKS）在目標(biāo)方面的差距百分比。根據(jù)問(wèn)題說(shuō)明，第一個(gè)目標(biāo)是車(chē)輛數(shù)，第二個(gè)目標(biāo)是行駛距離。

求解時(shí)間是指達(dá)到與最佳已知解決方案或預(yù)期目標(biāo)結(jié)果之間的某一差距所需的時(shí)間。求解時(shí)間是實(shí)際用例中最重要的標(biāo)準(zhǔn)之一，在預(yù)算時(shí)間內(nèi)獲得高準(zhǔn)確度的解決方案非常重要，組合優(yōu)化算法需要花費(fèi)大量時(shí)間。

圖 3 和圖 4 顯示了求解器在大型基準(zhǔn)測(cè)試實(shí)例子集上的收斂行為。

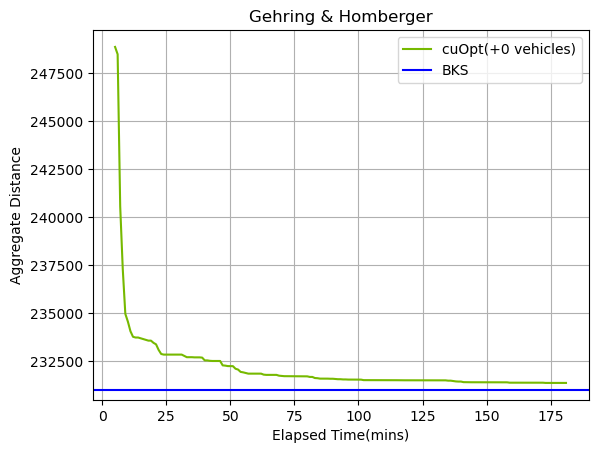
圖 3. cuOpt 在 CVRPTW 問(wèn)題上的收斂行為

我們從每個(gè)類(lèi)別（C1_10_1、C2_10_1、R1_10_1、R2_10_1、RC1_10_1、RC2_10_1）中選取了一個(gè)實(shí)例，以展示求解器的整體行為取決于（聚類(lèi)、隨機(jī)）和（長(zhǎng)路徑、短路徑）實(shí)例。我們將每分鐘采樣的總和與總 BKS 進(jìn)行比較。

隨著時(shí)間的推移，一開(kāi)始的急劇收斂會(huì)慢慢接近總 BKS。在這些實(shí)例集中，我們能夠匹配 BKS 的總車(chē)輛數(shù)，cuOpt 求解器幾乎可以在 Gehring 和 Homberger 的所有實(shí)例中找到 BKS 的車(chē)輛數(shù)，但實(shí)際性能取決于生成初始解決方案相比改進(jìn)階段所花費(fèi)的時(shí)間。

求解器在較大的實(shí)例中收斂速度很快，而在較小的實(shí)例中，收斂速度更是要快上幾個(gè)數(shù)量級(jí)。在下表中，我們展示了在達(dá)到與 BKS 相同的車(chē)輛數(shù)的同時(shí)，在不同規(guī)模的問(wèn)題上達(dá)到 BKS 所需的時(shí)間。

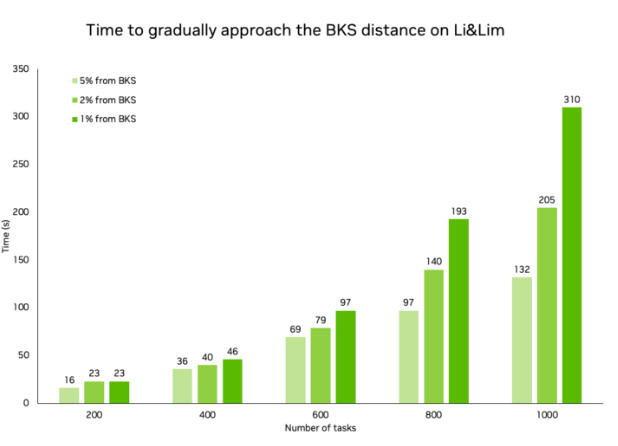
圖 4. PDPTW 問(wèn)題求解時(shí)間

cuOpt 創(chuàng)造 23 項(xiàng)世界紀(jì)錄

憑借使用 GPU 加速啟發(fā)式算法和最先進(jìn)的策略這一新方法，cuOpt 打破了 Gehring & Homberger 基準(zhǔn)測(cè)試中 15 個(gè)實(shí)例和 Li & Lim 基準(zhǔn)測(cè)試中 8 個(gè)實(shí)例的紀(jì)錄。

目前，NVIDIA 保持著過(guò)去三年 CVRPTW 和 PDPTW 類(lèi)別的所有紀(jì)錄。

在圖 5 中，每條邊代表從一個(gè)任務(wù)到另一個(gè)任務(wù)的路徑。綠線代表與前一記錄相同的邊緣，藍(lán)色和紅色邊代表兩個(gè)解決方案之間的差異。由于采用了進(jìn)化策略，cuOpt 解決方案在可能解的搜索空間中處于完全不同的位置，這意味著存在許多不同的邊緣。

圖 5. cuOpt 世界紀(jì)錄與前紀(jì)錄的路徑可視化圖對(duì)比

來(lái)源：Combopt.org

Gehring & Homberger 與 BKS 的總體平均差距為 -0.07% 距離差距和 0.29% 車(chē)輛數(shù)差距。Li & Lim 與 BKS 的總體平均差距為 1.22% 距離差距和 0.36% 車(chē)輛數(shù)量差距。基準(zhǔn)測(cè)試在單顆 NVIDIA GPU 上運(yùn)行了 200 分鐘。

總結(jié)

NVIDIA cuOpt 利用 GPU 加速和 RAPIDS 等 NVIDIA 技術(shù)，在數(shù)秒內(nèi)即可獲得高質(zhì)量的解決方案。我們的局部搜索運(yùn)行速度較基于 CPU 的方法提高了 100 倍，基于 CPU 的求解器需要數(shù)小時(shí)才能獲得類(lèi)似的解決方案。

審核編輯：劉清