今日正文

(1) 什么是線性時不變系統(LTI System)?

線性時不變系統，英文全稱是linear time-invariant system，簡稱LTI System。

線性時不變系統，即這個系統既是線性系統，又是時不變系統。

所謂線性系統，即表示系統滿足疊加關系，如下圖所示。

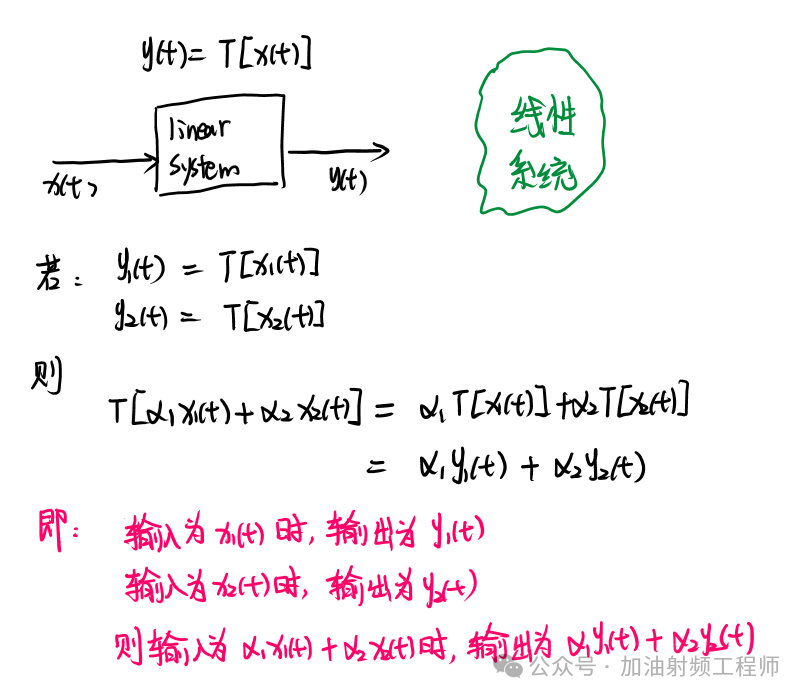
所謂時不變系統，即滿足下列等式，如下圖所示：

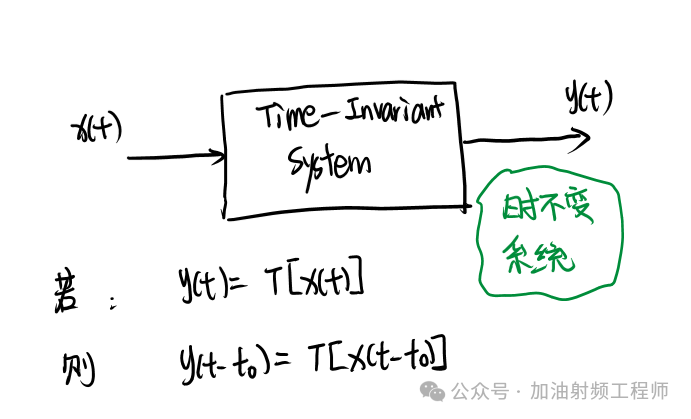
即，輸入的時延會等量的反應到輸出上。

(2)線性時不變系統的傳輸函數

線性時不變系統，可以用系統的沖激響應來表示，即當輸入為沖激函數δ(t)時，系統的輸出響應。同時結合LTI系統所滿足的線性和時不變特性，推導出輸入x(t)，輸出y(t)和沖激響應h(t)之間的關系，如下圖所示。可以看到，LTI系統的輸出，是其輸入與系統沖激響應的卷積。

對等式兩端求傅里葉變換，可以得到：

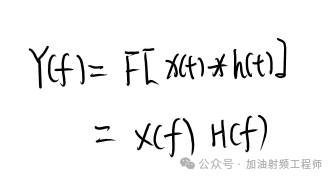
H(f)即定義為LTI系統的傳輸函數，為Y(f)和X(f)的比值，也為系統的沖激響應對應的傅里葉變換，即：

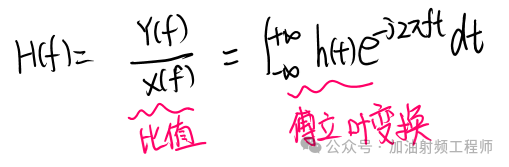
同時，傳輸函數H(f)還可以分成兩部分來表示，一部分為幅度，一部分為相位，即：

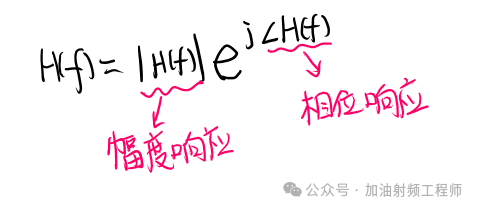
(3)無失真線性時不變系統

對于小信號射頻鏈路而言，我們希望這個線性時不變系統是無失真的，即信號通過這個系統時，相當于把信號從一個時間點上平移到另一個時間點上，除了幅度等比例放大或縮小外，其他都不變。

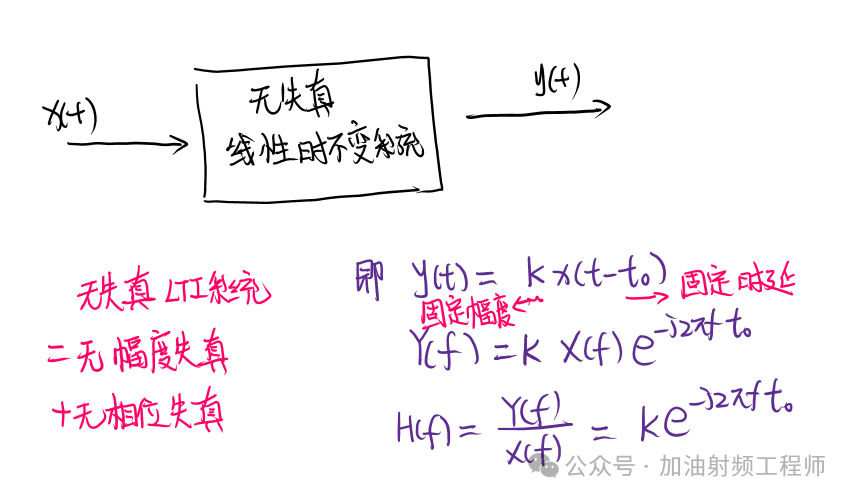
無失真線性時不變系統，即表示既無幅度失真，也無相位失真。

所謂幅度失真，就是不同頻率處幅度的放大或縮小的比例不一致，即上圖中的K隨頻率變化。所謂相位失真，就是不同頻率處相位時延(phase delay)不一致，即上圖中的t0隨頻率變化。

而無幅度失真和無相位失真，即表示K和t0都是恒定值。

無失真線性時不變系統的傳輸函數H(f)的幅度和相位響應，可以用下圖來表示。

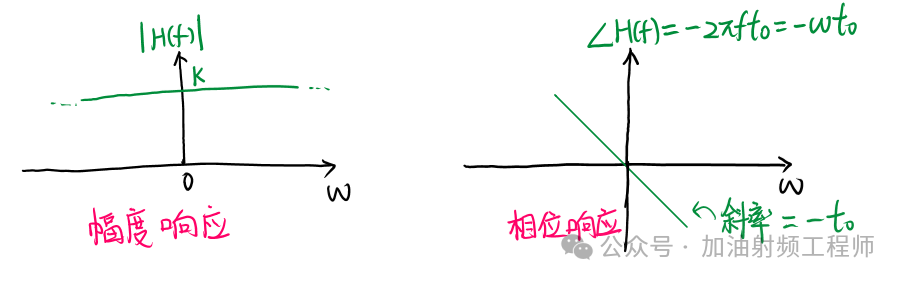
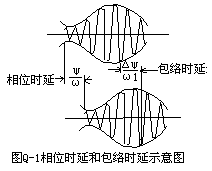
(4) group delay和phase delay的定義

群時延(group delay)和相位時延(phase delay)的定義如上圖所示。

按照上面的定義，計算無失真線性時不變系統傳輸函數對應的phase delay和group delay，發現兩者是相等的，如下圖所示。

(5)那群時延和相位時延分別是怎么影響著信號的呢？

假設輸入是一個帶包絡的窄帶調制信號，那么可以推導出這個信號經過LTI系統后，群時延和相位時延對它的影響，如下圖所示。

(6)從頻域看看這個影響？

假設系統為無失真線性時不變系統，則τp=τg，并假設輸入信號是帶包絡的窄帶調制信號，如下圖所示。

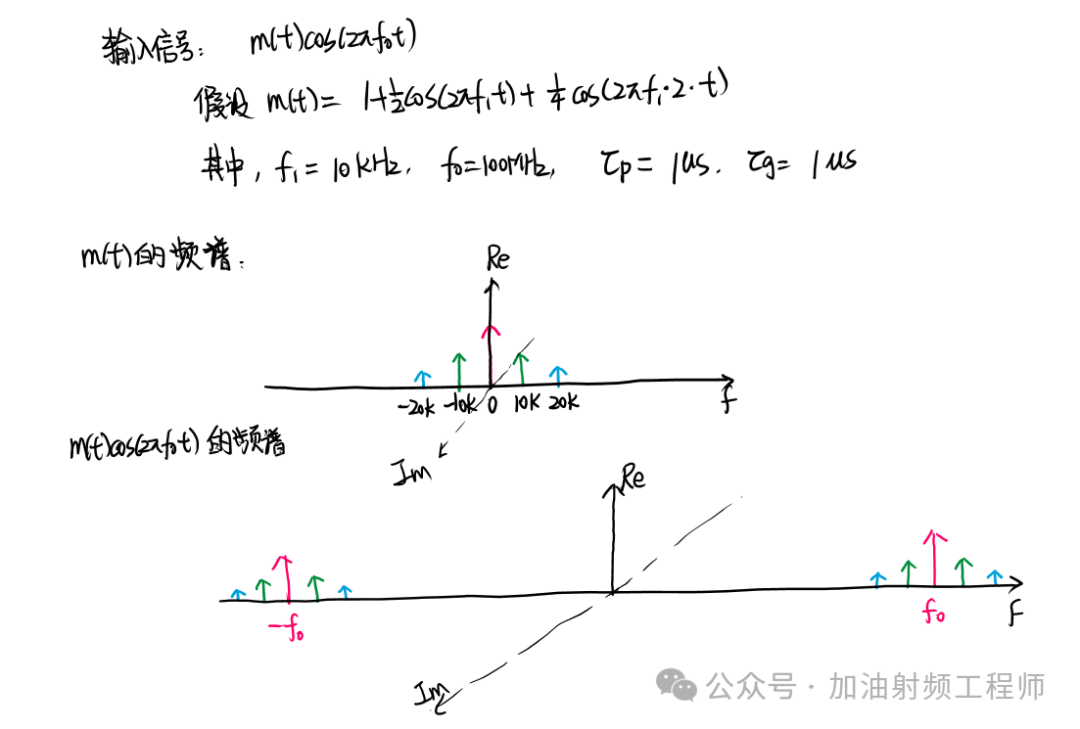
則輸出信號的頻譜為：

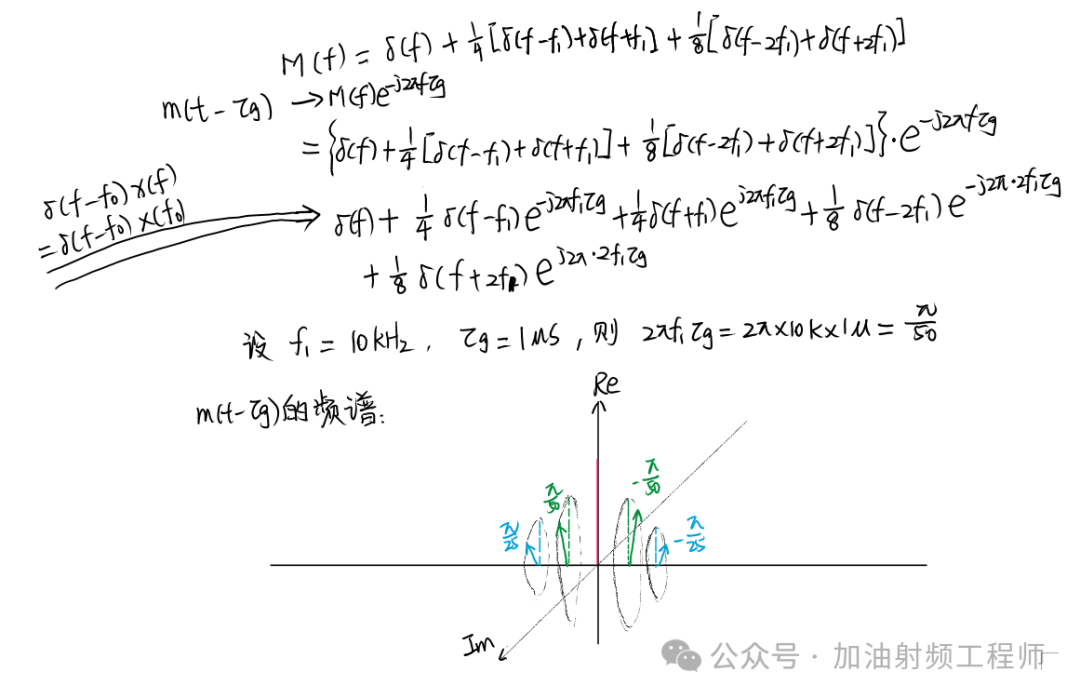
在相應的假設下，輸出信號的頻譜為：

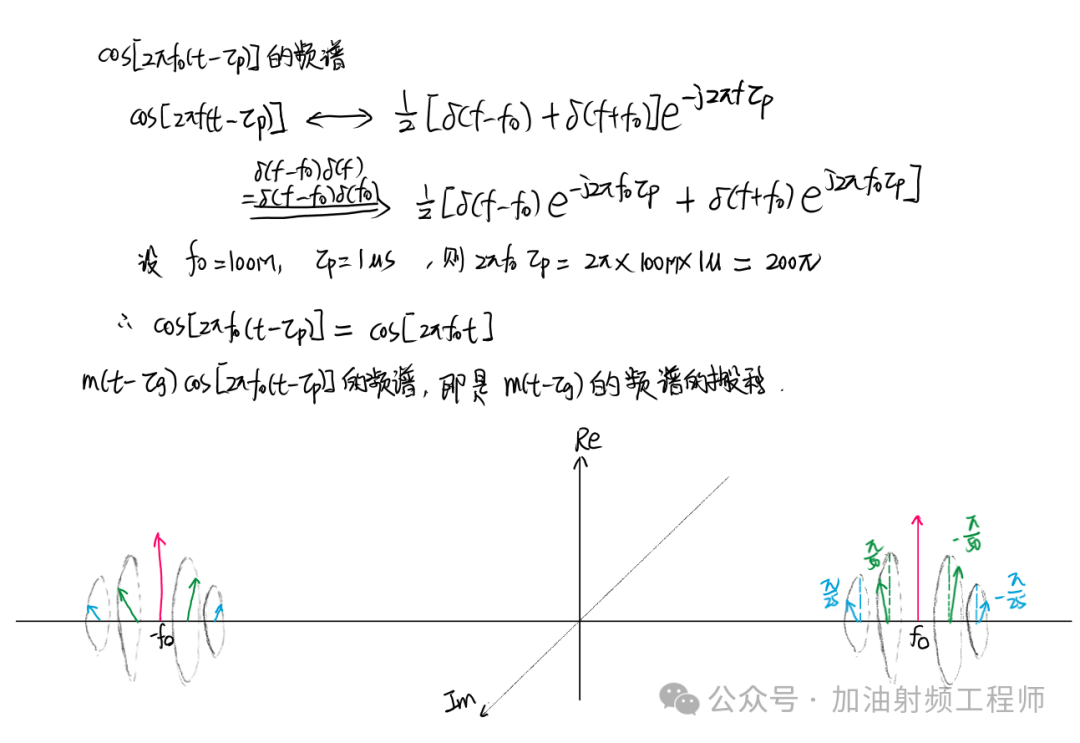
也就是說，group delay對應于m(t)個頻率分量的角度旋轉，上面是假設τg是不隨頻率變化的，旋轉角度是有規律可言的；但一般濾波器的群時延，都有一個波動，這會導致旋轉角度沒有規律，而且基帶頻率的地方，角度旋轉的越多。不知道，這是不是寬帶信號要求群時延波動更低的底層原因？

而phase delay則對應于載波的角度旋轉，因為這邊的假設，載波的旋轉角度正好是200pi，正好是周期的整數倍，所以沒有在圖中體現出旋轉角度的量。

我想基帶算法部分，對固定的群時延應該能夠糾正，但是對于群時延波動，不知道行不行？