均值濾波也稱為線性濾波,其采用的主要方法為鄰域平均法。線性濾波的基本原理是用均值代替原圖像中的各個像素值,即對待處理的當前像素點(x,y),選擇一個模板,該模板由其近鄰的若干像素組成,求模板中所有像素的均值,再把該均值賦予當前像素點(x,y),作為處理后圖像在該點上的灰度g(x,y),即g(x,y)=∑f(x,y)/m,m為該模板中包含當前像素在內的像素總個數。這本是數字圖像處理的一種方法,但也可以用在我們數字電壓電流表的ADC采樣數據上。我們選取二十次的ADC采樣值存儲在數組 Volt_Buffer 中,然后去除掉數組中的最大值和最小值后再取平均,得到的值作為結果顯示在數碼管上,這樣可以較大程度獲得準確的、不易波動的數據。程序在實驗五的基礎上略作修改即可,首先是增加和修改變量:
#define ADC_SAMPLE_SIZE (20) //規定采樣20個數據用來濾波 uint16_t Volt_Buffer[ADC_SAMPLE_SIZE]; //存儲ADC轉換值 uint32_t Led_Dis_Time; //計數,300ms改變一次數碼管顯示值
接下來是均值濾波的主體函數:
uint32_t Mean_Value_Filter(uint16_t *value, uint32_t size) //均值濾波 { uint32_t sum = 0; //ADC采樣數據和 uint16_t max = 0; uint16_t min = 0xffff; //min初值取最大是為了將第一個數據記錄 int i; for(i = 0; i < size; i++) { sum += value[i]; if(value[i] > max) { max = value[i]; } if(value[i] < min) { min = value[i]; } } sum -= max + min; //去除最大最小值 sum = sum / (size - 2); return sum; }
對之前的電壓計算函數 Volt_Cal() 修改如下:
void Volt_Cal(void)
{
Cal_Buffer = Mean_Value_Filter(Volt_Buffer,ADC_SAMPLE_SIZE);
Cal_Buffer = (Cal_Buffer * ADC_REF_VALUE >> 12) * (R2 + R1)/R1;
// 四舍五入
if(Cal_Buffer % 10 >= 5)
{
Cal_Buffer = Cal_Buffer / 10 + 1;
}
else
{
Cal_Buffer = Cal_Buffer / 10;
}
}
在主函數的 while 循環里每隔300ms刷新一次:
while(1)
{
if(GetTick() >= (Led_Dis_Time + 300))
{
Led_Dis_Time = GetTick();
Volt_Cal();
Display(Cal_Buffer);
}
}
在之前未加濾波函數時,數碼管上顯示的電壓數據是不穩定、跳變的,而加了濾波函數之后,數碼管顯示的電壓數據可以穩定下來,并且有一定的抗干擾能力。至于電壓準確性的問題,在后續章節的數據標定和校準中說明。
審核編輯 黃宇
-
數據處理
+關注
關注
0文章
626瀏覽量
29099 -
濾波算法
+關注
關注
2文章
89瀏覽量
13928 -
均值濾波
+關注
關注
0文章
10瀏覽量
7196 -
電壓電流表
+關注
關注
0文章
25瀏覽量
2180 -
CW32
+關注
關注
1文章
243瀏覽量
1174
發布評論請先 登錄
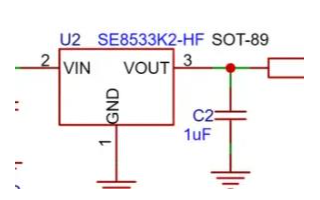
CW32數字電壓電流表-產品硬件設計要點
如何去使用數字信號處理算法
CW32數字電壓電流表軟件教程(七):基本數據處理算法(均值濾波)
CW32數字電壓電流表軟件教程-實驗四:數碼管動態顯示

CW32數字電壓電流表軟件教程-實驗五:ADC采樣及顯示
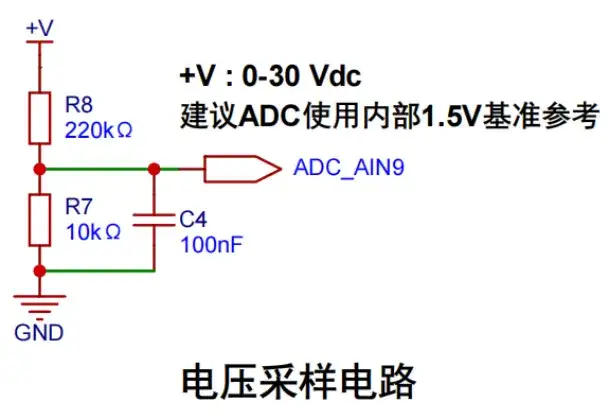
CW32數字電壓電流表軟件進階教程-2.電壓電流值做均值濾波
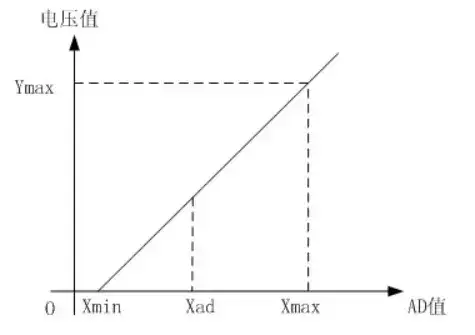
CW32數字電壓電流表軟件進階教程-3.電壓電流標定























評論