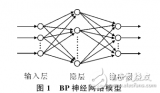
BP神經網絡算法，即反向傳播神經網絡算法，是一種常用的多層前饋神經網絡訓練算法。它通過反向傳播誤差來調整網絡的權重和偏置，從而實現對輸入數據的分類或回歸。下面詳細介紹BP神經網絡算法的基本流程。

1. 初始化網絡參數

在BP神經網絡算法中，首先需要初始化網絡的參數，包括權重和偏置。權重是連接神經元之間的系數，偏置是神經元的閾值。權重和偏置的初始值通常設置為小的隨機數，以避免對稱性問題。

1.1 隨機初始化權重

權重的初始化是BP神經網絡算法的關鍵步驟之一。權重的初始值通常設置為小的隨機數，例如在[-0.1, 0.1]范圍內的隨機數。權重的初始化方法有多種，如均勻分布、正態分布等。權重的初始化方法會影響網絡的收斂速度和性能。

1.2 初始化偏置

偏置的初始化通常設置為0或小的隨機數。偏置的值對網絡的收斂速度和性能也有一定的影響。

2. 前向傳播

前向傳播是BP神經網絡算法的核心步驟之一。在前向傳播過程中，輸入數據通過隱藏層和輸出層進行計算，得到網絡的輸出值。

2.1 輸入層

輸入層是BP神經網絡的第一層，負責接收輸入數據。輸入層的神經元數量與輸入數據的特征數量相同。

2.2 隱藏層

隱藏層是BP神經網絡的中間層，負責提取輸入數據的特征。隱藏層的神經元數量可以根據問題的復雜度和數據量進行調整。隱藏層的激活函數通常使用Sigmoid函數、Tanh函數或ReLU函數等。

2.3 輸出層

輸出層是BP神經網絡的最后一層，負責生成網絡的輸出值。輸出層的神經元數量與問題的輸出類別數量相同。輸出層的激活函數通常使用Softmax函數或線性函數等。

3. 計算誤差

在前向傳播過程中，網絡的輸出值與實際值之間存在誤差。計算誤差是BP神經網絡算法的關鍵步驟之一。

3.1 誤差函數

誤差函數是衡量網絡輸出值與實際值之間差異的函數。常用的誤差函數有均方誤差函數（MSE）、交叉熵誤差函數（Cross-Entropy）等。誤差函數的選擇取決于問題的類型和需求。

3.2 誤差反向傳播

誤差反向傳播是BP神經網絡算法的核心步驟之一。在誤差反向傳播過程中，誤差從輸出層反向傳播到輸入層，通過鏈式法則計算每個權重和偏置對誤差的貢獻。

3.2.1 計算輸出層的誤差梯度

在輸出層，誤差梯度可以通過誤差函數的導數計算得到。例如，對于均方誤差函數，誤差梯度為：

?E/?o = (o - t)

其中，o表示輸出值，t表示實際值。

3.2.2 計算隱藏層的誤差梯度

在隱藏層，誤差梯度可以通過鏈式法則計算得到。對于第j個神經元，其誤差梯度為：

?E/?zj = ?E/?oj * ?oj/?zj

其中，zj表示第j個神經元的輸入值，oj表示第j個神經元的輸出值。

3.2.3 更新權重和偏置

根據誤差梯度，可以使用梯度下降法或其他優化算法更新網絡的權重和偏置。權重和偏置的更新公式為：

w_new = w_old - α * ?E/?w

b_new = b_old - α * ?E/?b

其中，w表示權重，b表示偏置，α表示學習率。

4. 迭代訓練

BP神經網絡算法通常需要多次迭代訓練，以優化網絡的性能。在每次迭代中，都需要進行前向傳播、計算誤差、誤差反向傳播和更新權重偏置等步驟。

4.1 學習率調整

學習率是BP神經網絡算法中的一個重要參數，它決定了權重和偏置更新的幅度。學習率過大可能導致網絡訓練不穩定，學習率過小可能導致訓練時間過長。在訓練過程中，可以根據網絡的性能調整學習率。

4.2 早停法

早停法是一種防止過擬合的方法。在訓練過程中，可以使用驗證集評估網絡的性能。當驗證集的性能不再提高時，可以提前停止訓練，以避免過擬合。

5. 模型評估

在訓練完成后，需要對模型進行評估，以驗證其性能。常用的評估指標有準確率、召回率、F1分數等。評估指標的選擇取決于問題的需求和類型。