在數(shù)字信號處理領(lǐng)域,IIR(無限脈沖響應(yīng))系統(tǒng)和FIR(有限脈沖響應(yīng))系統(tǒng)是兩種常用的濾波器類型。它們在設(shè)計、性能和應(yīng)用方面都存在顯著差異。
1. 數(shù)學(xué)基礎(chǔ)
1.1 IIR系統(tǒng)
IIR系統(tǒng)是一種遞歸濾波器,其輸出不僅取決于當(dāng)前和過去的輸入值,還取決于當(dāng)前和過去的輸出值。IIR系統(tǒng)的數(shù)學(xué)表達(dá)式可以表示為:
[ y[n] = -sum_{k=1}^{N} a_k y[n-k] + sum_{k=0}^{M} b_k x[n-k] ]
其中,( y[n] ) 是輸出信號,( x[n] ) 是輸入信號,( a_k ) 和 ( b_k ) 分別是濾波器系數(shù),( N ) 和 ( M ) 分別是濾波器的階數(shù)。
1.2 FIR系統(tǒng)
與IIR系統(tǒng)不同,F(xiàn)IR系統(tǒng)是一種非遞歸濾波器,其輸出僅取決于當(dāng)前和過去的輸入值,而與過去的輸出值無關(guān)。FIR系統(tǒng)的數(shù)學(xué)表達(dá)式可以表示為:
[ y[n] = sum_{k=0}^{M} b_k x[n-k] ]
其中,( y[n] ) 是輸出信號,( x[n] ) 是輸入信號,( b_k ) 是濾波器系數(shù),( M ) 是濾波器的階數(shù)。
2. 設(shè)計方法
2.1 IIR系統(tǒng)設(shè)計
IIR系統(tǒng)的設(shè)計通常涉及兩個主要步驟:確定濾波器的階數(shù)和系數(shù)。設(shè)計方法包括:
- 脈沖響應(yīng)法 :通過給定的脈沖響應(yīng)來確定濾波器的系數(shù)。
- 頻率響應(yīng)法 :通過給定的頻率響應(yīng)來確定濾波器的系數(shù)。
- 最小二乘法 :通過最小化誤差來確定濾波器的系數(shù)。
- 優(yōu)化方法 :通過優(yōu)化算法(如遺傳算法、粒子群優(yōu)化等)來確定濾波器的系數(shù)。
2.2 FIR系統(tǒng)設(shè)計
FIR系統(tǒng)的設(shè)計通常涉及三個主要步驟:確定濾波器的階數(shù)、窗函數(shù)和系數(shù)。設(shè)計方法包括:
- 窗函數(shù)法 :通過給定的窗函數(shù)來確定濾波器的系數(shù)。
- 頻率采樣法 :通過給定的頻率采樣點來確定濾波器的系數(shù)。
- 最小二乘法 :通過最小化誤差來確定濾波器的系數(shù)。
- 優(yōu)化方法 :通過優(yōu)化算法(如遺傳算法、粒子群優(yōu)化等)來確定濾波器的系數(shù)。
3. 穩(wěn)定性
3.1 IIR系統(tǒng)穩(wěn)定性
IIR系統(tǒng)的穩(wěn)定性取決于其系數(shù)。如果所有極點都位于單位圓內(nèi),則IIR系統(tǒng)是穩(wěn)定的。然而,IIR系統(tǒng)的穩(wěn)定性較難保證,因為其系數(shù)可能會受到設(shè)計方法和參數(shù)選擇的影響。
3.2 FIR系統(tǒng)穩(wěn)定性
與IIR系統(tǒng)不同,F(xiàn)IR系統(tǒng)總是穩(wěn)定的。這是因為FIR系統(tǒng)的極點都位于原點,這意味著它們不會對系統(tǒng)的穩(wěn)定性產(chǎn)生影響。
4. 頻率響應(yīng)
4.1 IIR系統(tǒng)頻率響應(yīng)
IIR系統(tǒng)的頻率響應(yīng)可以通過其系數(shù)和階數(shù)來確定。IIR系統(tǒng)的頻率響應(yīng)通常具有更復(fù)雜的形狀,這使得它們在某些應(yīng)用中具有優(yōu)勢。然而,IIR系統(tǒng)的頻率響應(yīng)也可能導(dǎo)致相位失真和振鈴效應(yīng)。
4.2 FIR系統(tǒng)頻率響應(yīng)
FIR系統(tǒng)的頻率響應(yīng)可以通過其系數(shù)和窗函數(shù)來確定。FIR系統(tǒng)的頻率響應(yīng)通常具有線性相位特性,這意味著它們在處理信號時不會產(chǎn)生相位失真。然而,F(xiàn)IR系統(tǒng)的頻率響應(yīng)可能在某些應(yīng)用中不夠靈活。
-
濾波器
+關(guān)注
關(guān)注
162文章
8133瀏覽量
181901 -
數(shù)字信號處理
+關(guān)注
關(guān)注
16文章
567瀏覽量
46710 -
FIR
+關(guān)注
關(guān)注
4文章
151瀏覽量
34231 -
IIR
+關(guān)注
關(guān)注
1文章
62瀏覽量
23192
發(fā)布評論請先 登錄
FIR濾波器與IIR濾波器的區(qū)別與特點
FIR濾波器與IIR濾波器的區(qū)別與特點
FIR濾波器和IIR濾波器有什么區(qū)別
一文讀懂FIR濾波器與IIR濾波器的區(qū)別
簡談FIR濾波器和IIR濾波器的區(qū)別
詳解FIR濾波器和IIR濾波器的區(qū)別
詳解FIR濾波器和IIR濾波器區(qū)別
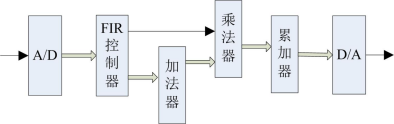
IIR與FIR濾波器的比較和區(qū)別
FIR濾波器與IIR濾波器到底有什么區(qū)別

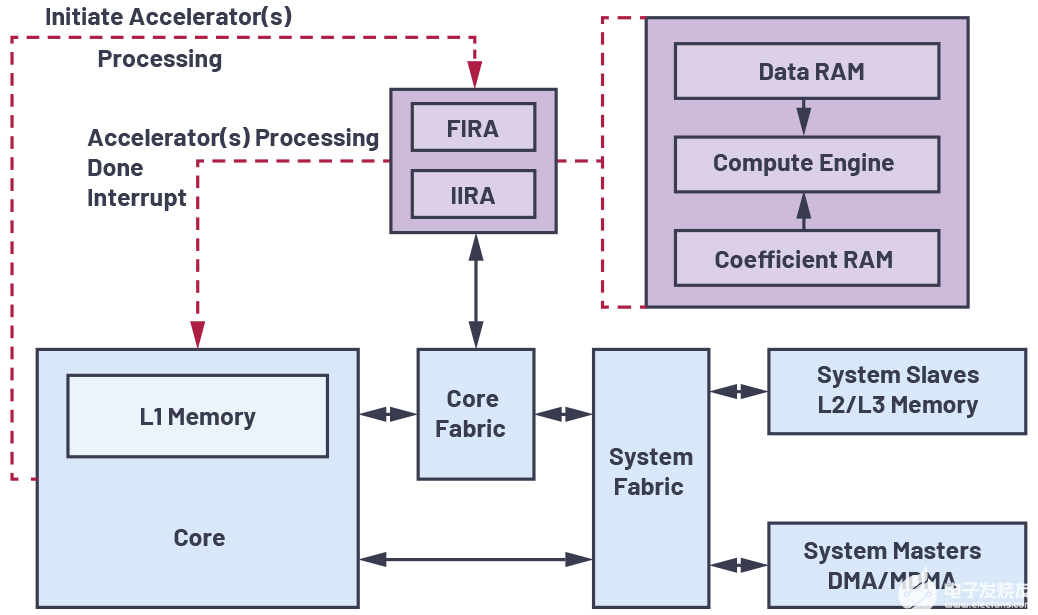
利用數(shù)字信號處理器上的片上FIR和IIR硬件加速器



















評論